Другие формулировки

Подобный смысл имеют другие логические законы, многие из которых сложились исторически. В частности, закон двойного отрицания и закон Пирса эквивалентны закону исключённого третьего. Это означает, что расширение системы аксиом интуиционистской логики любым из этих трёх законов в любом случае приводит к классической логике. И всё же, в общем случае, существуют логики, в которых все три закона неэквивалентны.

Примеры:

Предположим, что P представляет собой утверждение «Сократ смертен». Тогда закон исключённого третьего для P примет вид: «Сократ смертен или Сократ бессмертен», откуда ясно, что закон отсекает все иные варианты, при которых Сократ и не смертен и не бессмертен. Последнее — это и есть то самое «третье», которое исключается.

Гораздо более тонкий пример применения закона исключённого третьего, который хорошо демонстрирует, почему он не является приемлемым с точки зрения интуиционизма, состоит в следующем. Предположим, что мы хотим доказать теорему, что существуют иррациональные числа a и b, такие что рационально. Известно, что иррационально. Рассмотрим. Если данное число рационально, то теорема доказана. Иначе возьмём 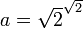и. Тогда 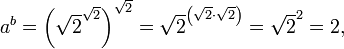то есть рациональное число. По закону исключённого третьего иных вариантов быть не может. Поэтому, теорема в общем случае доказана. Причём доказательство предельно просто и элементарно. С другой стороны, если принять интуиционистскую точку зрения и отказаться от закона исключённого третьего, теорема хотя и может быть доказана, но доказательство её становится исключительно сложным.

Поправка: доказательство того факта, что иррациональное число в иррациональной степени может быть рациональным, может быть проведено элементарным способом. Он не требует использования каких-то глубоких результатов из теории чисел. А именно, в качестве первого числа возьмём корень квадратный из двух, а второе число пусть будет равно удвоенному логарифму 3 по основанию 2. Очевидно, что при возведении в степень получается рациональное число 3. При этом как основание степени, так и показатель иррациональны. Доказательство того, что логарифм иррационален, состоит в том, что если бы он равнялся m/n, то 2 в степени m было бы равно 3 в степени n, что невозможно.

Date: 2015-08-15; view: 440; Нарушение авторских прав