Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теоретичні відомості
|
|
 |
Дифракційна решітка - це пристрій, що має N однакових паралельних щілин на рівних відстанях одна від одної. Здебільшого дифракційна решітка може бути у вигляді плоскої скляної поверхні, на якій спеціальною машиною нанесено досить багато (інколи сотні тисяч) прямих рівновіддалених штрихів. На таких решітках спостереження можна вести в світлі, що проходить і у відбитому світлі.
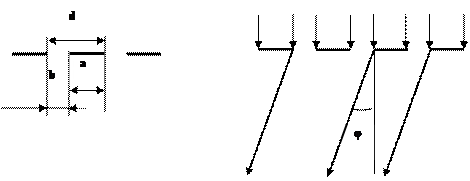
Переріз плоскої решітки має вигляд, що показаний на мал.1, де a - ширина штриха, b - ширина щілини, d=a+b - стала, або період дифракційної решітки, d=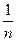 
, де n - кількість штрихів на одиницю довжини решітки, j - кут дифракції.
Якщо на решітку нормально до її площини падає плоска монохроматична хвиля довжиною l, то на кожній з щілин b відбувається дифракція світла і кожна щілина стає джерелом циліндричної хвилі. Оскільки стала решітки досить мала (0,01мм), то хвилі, що йдуть від сусідніх щілин будуть когерентні і можуть інтерферувати. Розрахунок інтерференції світла від усіх N щілин дифракційної решітки дає вираз для інтенсивності світла, що поширюється під кутом j до нормалі:
Ij=I0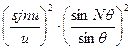 
(1)
де u=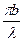 
.sinj, 
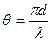.sinj, I0 - інтенсивність світла, що проходить через одну щілину, коли j=0 Формула (1) - основна в теорії дифракційної решітки. Перший множник характеризує розподіл інтенсивності при дифракції плоскої хвилі на кожній щілині, а другий враховує інтерференцію між пучками, що дифрагують під кутом j від N щілин.
Графік функції Ij(sinj) має вигляд, що даний на мал.2. Подібна дифракційна картина спостерігається у фокальній площині лінзи, яку розташовують за дифракційною решіткою.
 |
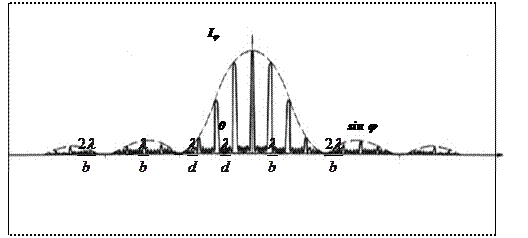Мал.2 Графік функції Ij(sinj)
Пунктирна обвідна відповідає розподілу інтенсивності при дифракції на одній щілині, помноженій на N2(Ilj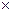 
N2). Тому положення головних мінімумів знаходять з умови мінімумів на одній щілині.
b×sinj=±m×l (2)
де m=1,2….. визначає порядок мінімуму.
Аналізуючи вираз (1) можна також показати, що головні максимуми спостерігаються під кутами дифракції j, які задовольняють умові:
d×sinj=±m×l (3),
де m=!, 2,…і визначає порядок максимуму.
Ці максимуми є результатом інтерференції світла від сусідніх щілин. Якщо в результаті такої інтерференції хвилі гасять одна одну, то виникають додаткові мінімуми між сусідніми головними максимумами, їх число дорівнює (N-1) і умовою додаткового мінімуму є
d×sinj=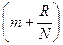 
×l (4)
де R=1, 2, …, N-1
Картина, що показана на Мал.2 спостерігається в монохроматичному світлі. Якщо дифракційну решітку освітлювати білим світлом, то побачимо картину, що є результатом накладання таких картин для різних довжин хвилі. Замість вузьких максимумів
1, 2, …порядків (при sinj=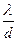 
; 
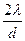;…) побачимо спектри відповідно першого, другого та ін. порядків. Максимум нульового порядку (sinj=o) буде білого кольору, тому що тут накладаються максимуми для всіх довжин хвиль.
Як бачимо, дифракційна решітка є спектральним приладом і характеризується роздільною здатністю R та кутовою дисперсією D.
Найменша різниця довжин хвиль двох спектральних ліній dl, при яких спектральний прилад розділяє їх окремо, називається спектральною роздільною відстанню, а величина
R=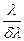 
- роздільною здатністю приладу. (5)
Спектральні лінії вважаються розділеними (за критерієм Релея), коли головний максимум лінії збігається з першим додатковим мінімумом того ж порядку для другої довжини хвилі (Мал.3). Це означає, що
d×sinj=m×(l+dl)
d×sinj=(m+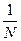 
)×l
тоді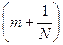 
×l=m×(l+dl)
dl=l¢-l=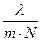 
, звідки
R=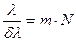 
(6)
 |
Як видно, роздільна здатність решітки залежить від загальної кількості її штрихів і зростає з порядком спектру. Кутовою дисперсією називається величина
D=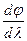 
(7),
де dj кутова відстань між двома спектральними лініями, яким відповідають довжини хвиль li=l+dl.. Для визначення D продиференціюємо формулу (3), тоді d×cosj×dj=m×dl, звідки
D=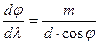 
(8)
Для малих кутів дифракції j маємо cos j»1;
D=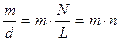 
(9)
де L - довжина робочої ділянки решітки. Дисперсія решітки визначається її сталою d і зростає з порядком хвилі, тобто дифракційний спектр рівномірний для всіх довжин хвиль, в цьому його перевага перед спектром, одержаним від призми, який розтягнутий у фіолетовій, стиснутий у червоній частини спектру.
Date: 2015-08-07; view: 369; Нарушение авторских прав