Краткая теория. В конце 19 века и начале 20 столетия в физике были проведены эксперименты, которые сыграли решающую роль в переходе от классических представлений к идеям

В конце 19 века и начале 20 столетия в физике были проведены эксперименты, которые сыграли решающую роль в переходе от классических представлений к идеям современной физики и легли в основу квантовой механики и атомной теории.

В 1900 году Макс Планк рассматривая процессы излучения

абсолютно черным телом, пришел к выводу, что излучение и

- 3 -

поглощение энергии «атомными осцилляторами», совершающи-ми колебания с частотой n, происходят не непрерывно, а отдельными порциями - «квантами энергии» величина которых равна E=hn (здесь h –постоянная Планка, равная 6,62×10^-34 Дж×с). В 1905 году Альберт Эйнштейн, объясняя явление фотоэффекта, предложил считать, что свет состоит из квантов (фотонов), несущих энергию hn и летящих в пространстве со скоростью света. Теория, прекрасно описывающая фотоэффект и излучение света черным телом, не давала ответа на вопрос: является ли дискретность энергетических состояний свойством лишь «атомных осцилляторов» в твердом теле или эта дискретность присуща и изолированным атомам?

В 1913 году Нильс Бор предложил модель атома, состоящего из ядра и вращающихся вокруг него электронов. Так как электрон в атоме движется с ускорением, то, согласно классической теории, атом должен непрерывно излучать энергию, электрон будет по спирали приближаться к ядру, а частота излучаемых им электромагнитных волн непрерывно увеличиваться. Спектр излучения должен быть сплошным, что противоречило опытным данным. Чтобы устранить эти противоречия Бор сформулировал три постулата:

1. Постулат стационарных состояний. Электрон в атоме может находиться не в любых состояниях, а лишь в состоя-ниях с энергиями образующими дискретный ряд: Е₁, E₂,., E_n.

2. Условие квантования орбит. Момент импульса (количества движения) электрона, движущегося по разрешенной орбите, всегда квантован и кратен главному квантовому числу n:

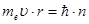, (1)

где 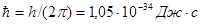- постоянная Планка, 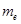‑ масса электрона, 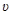‑скорость электрона.

3. Правило частот. При переходе электрона из одного разрешенного состояния в другое атом излучает или погло-щает квант энергии 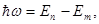(2)

где Е_n и E_m – энергия электрона соответственно на орбитах n и m, w - циклическая частота.

- 4 -

На основании своих постулатов Бор разработал элементарную теорию водородного атома. В простейшей форме, движение электрона в атоме происходит по круговой орбите радиуса r вокруг протона под действием силы Кулона. Уравнение такого движения имеет вид:

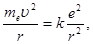(3)

где 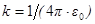- коэффициент пропорциональности.

Из (1) и (3) следует, что скорость электрона на n – й орбите

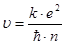, (4)

а радиус n – й орбиты:

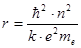. (5)

где = a₀ = 0,53×10^-10 м – боровский радиус.

Кинетическая энергия электрона на n – й орбите, с учетом (4)

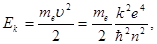(6)

Потенциальная энергия электрона на n – й орбите, с учетом (5)

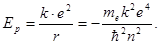(7)

Полная энергия электрона на n – й орбите, с учетом (6) и (7)

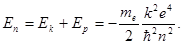(8)

Максимальное значение этой полной энергии равное нулю достигается при n = ¥. Как следует из (8) для удаления электрона от протона, т. е. ионизации атома водорода, необходима энергия Е =-13,6 эВ.

Формула (8) для энергетических уровней будет справедлива и для водородоподобных ионов (когда в поле положительного заряда ядра Ze остается всего один электрон)

- 5 -

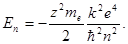
С учетом правила частот (1) поглощать и отдавать энергию атом может лишь порциями, переходя из n‑го состояния в m ‑тое

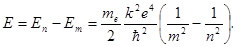(9)

Если энергию фотона выразить через длину волны 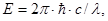то получим сериальную формулу:

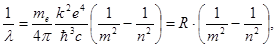(10)

где 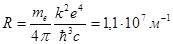- постоянная Ридберга.

Формула (10) идеально совпала с эмпирически найденной раннее Ридбергом сериальной формулой, с помощью которой были объяснены спектральные закономерности атома водорода. Кроме того, с помощью теории Бора был установлен состав постоянной Ридберга.

Опыты Джеймса Франка и Густава Герца выполненные в 1913 году показали существование у изолированных атомов дискретных уровней энергии и явились прямым подтверждением квантовых постулатов Бора. За эту работу им в 1925 году была присуждена Нобелевская премия.

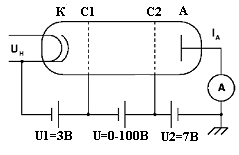Опыт Франка-Герца мож-но проиллюстрировать с помощью трубки, напол-ненной неоновым газом. Схема питания трубки приведена на рис.2. Элек-троны, излучаемые като-дом К и предварительно ускоренные между като-дом К и сеткой С1, влета-

т в регулируемое уско-

Рис.2

- 6 -

ряющее электрическое поле, созданное между сетками С1 и С2. Если энергия электрона меньше энергии возбуждения атома неона, то он испытывает упругие столкновения и преодолевает слабое тормозное поле между сеткой С2 и анодом А. В цепи амперметра течет ток. Однако при напряжении U на сетке С2, равном»16,8 В, кинетической энергии электрона достаточно, чтобы перевести валентный электрон неона на первый уровень возбуждения при неупругом ударе. В результате потери энергии электроны больше не могут преодолеть тормозное поле, что приводит к уменьшению величины тока. При дальнейшем уве-личении напряжения на сетке С2 кинетической энергии каждого электрона снова будет достаточно, чтобы преодолеть тормозное поле, при этом сила тока увеличивается. При напряжении U» 2х16,8 В значение кинетической энергии настолько велико, что два атома могут последовательно возбуждаться одним и тем же электроном, что соответствует второму минимуму (рис.3) и т.д.. Таким образом, на графике зависимости I от U представлены равноудаленные минимумы и максимумы.

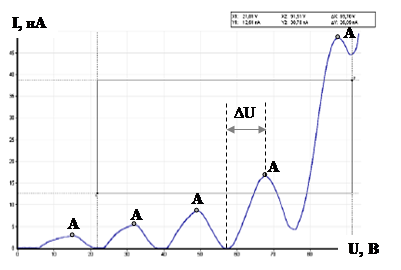
Рис.3 График зависимости тока в лампе от напряжения I(U)

- 7 -

Энергию возбуждения 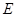атомов неона определяют по разнице напряжений в соседних минимумах или максимумах вольтамперной характеристики электронной лампы:

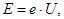(11)

где 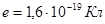- заряд электрона.

Возбужденный атом неона высвобождает поглощенную энергию, испуская фотон. При энергии возбуждения E длина волны и масса такого фотона соответственно равны:

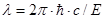, (12)

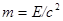, (13)

где 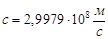- скорость света в вакууме.

Так как скорости электронов, покидающих раскаленный катод, подчиняются распределению Максвелла, то максимумы и минимумы вольтамперной зависимости четко не определены.

Электроны, имеющие максимальную скорость, раньше других начинают возбуждать атомы неона (на рис.3 точки А).

Для них закон сохранения энергии имеет вид:

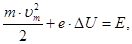(14)

где еDU- энергия, полученная электроном в электрическом поле.

Вокруг раскаленного катода находится объемный отрицатель-ный заряд (электронное облако). Полагая, что вылетевшие из облака электроны в направлении анода имеют начальную скоро-сть υ₀ и учитывая схему питания лампы, представим максималь-ную кинетическую энергию электрона в уравнении (14) как сумму энергий электрона при выходе его из электронного облака (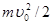) и полученной в пространстве катод – сетка С1 ():

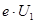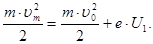(15)

Совместное решение уравнений (11), (14), (15) позволяет оценить начальную скорость:

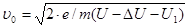. (16)

- 8 -

Количество электронов, испытавших упругие или неупругие

столкновения с атомами неона, можно оценить по зависимости тока в лампе от времени (рис.4).

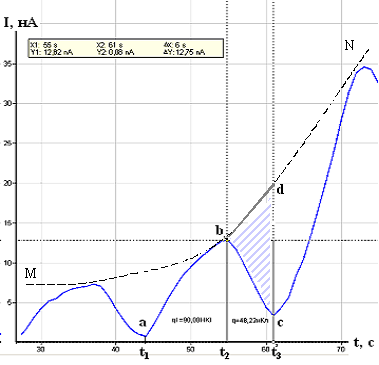
Рис.4 График зависимости тока в лампе от времени I(t)

Так, например, на участке ab протекающий через лампу заряд q_ab численно равен площади фигуры под кривой ab.

Площадь измеряется путем интегрирования, предусмотренного инструментами программы “Measure”.Разделив величину заряда на заряд электрона е можно оценить число электронов, испытав-ших упругие столкновения с атомами неона:

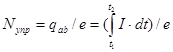. (17)

- 9 -

Аналогично оценивают число упруго сталкивающихся электронов с атомами неона и на участке bc зависимости I(t).

Если бы неупругие столкновения электронов с атомами неона отсутствовали, то ток в лампе нарастал бы по линии MN.

Так, например, на временном интервале t₂-t₃ ток в лампе нарастал бы по линии bd (см. рис.4) и через лампу протек бы заряд q_bd, численно равный площади трапеции (t₂ b d t₃)_.

Если из этого заряда вычесть реально протекающий заряд на участке bc и результат разделить на заряд электрона, то оценим количество электронов, испытавших неупругие столкновения с атомами неона:

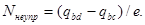(18)

Date: 2015-07-27; view: 385; Нарушение авторских прав