Убежденно разрывая ткань пространства

У физики есть одна захватывающая особенность: уровень понимания этой науки может измениться буквально за одну ночь. На следующее утро после того, как Строминджер послал свою статью в электронную базу данных, я скачал ее из Интернета и прочел в своем кабинете в Корнелле. Используя новые достижения теории струн, Строминджер одним махом разрешил считавшийся одним из самых запутанных вопрос о свертывании лишних измерений в пространство Калаби— Яу. Но после того как я разобрался в статье, мне пришло в голову, что он, возможно, раскрыл лишь половину того, что могло стоять за этой проблемой.

В описанной в главе 11 более ранней работе о флоп-перестройках с разрывом пространства мы исследовали двухэтапный процесс, в котором двумерная сфера стягивается в точку, приводя к разрыву структуры пространства, а затем раздувается по другим законам, приводя к восстановлению этой структуры. В своей статье Строминджер исследовал, что происходит при сжатии в точку трехмерной сферы; он показал, что благодаря открытым недавно протяженным объектам в теории струн физические свойства остаются хорошо определенными. И на этом его работа заканчивалась. Но нельзя ли исследовать второй этап, включающий, как и ранее, разрыв пространства и его последующее восстановление путем раздутия сфер?

Во время весеннего семестра 1995 г. у меня в Корнелле гостил Дейв Моррисон, и в тот день мы встретились, чтобы обсудить статью Строминджера. Через пару часов нам в общих чертах уже было понятно, что представляет собой второй этап. Вспомнив как Канделас, Грин и Тристан Хюбш (в то время работавший в Техасском университете в Остине) использовали некоторые результаты конца 1980-х гг., полученные математиками Гербом Клеменсом из университета штата Юта, Робертом Фридманом из Колумбийского университета и Майлсом Рейдом из университета в Уорвике, мы поняли, что при коллапсе трехмерной сферы возможен разрыв пространства Калаби—Яу и его последующее восстановление при повторном раздутии сферы. Но здесь нас ожидал сюрприз. Коллапсирующая сфера имела три измерения, а раздувающаяся — всего лишь два. Сложно описать, как это выглядит, но можно проиллюстрировать идею, пользуясь аналогией с меньшим числом измерений. Вместо того чтобы пытаться представить коллапс трехмерной сферы и ее замещение двумерной сферой, представим себе коллапс одномерной сферы и ее замещение нульмерной.

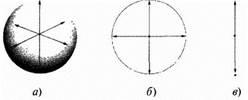
Рис. 13.2. Сферы разных размерностей, допускающих наглядное изображение: а) двумерная, 6) одномерная, в) нульмерная

Прежде всего, что такое одномерная или нульмерная сфера? Будем рассуждать по аналогии. Двумерная сфера — это совокупность точек трехмерного пространства, расположенных на одинаковых расстояниях от выбранного центра, как показано на рис. 13.2 а. По аналогии с этим, одномерная сфера есть совокупность точек двумерного пространства (например, поверхности этой страницы), расположенных на одинаковых расстояниях от выбранного центра. Как показано на рис. 13.25, это просто окружность. Наконец, согласно той же аналогии нульмерная сфера есть совокупность точек одномерного пространства (прямой линии), расположенных на одинаковых расстояниях от общего центра. Таким образом, аналогия с меньшим числом измерений, упоминавшаяся в предыдущем параграфе, приводит к окружности (одномерной сфере), которая стягивается, затем происходит разрыв пространства, и окружность замещается нульмерной сферой (двумя точками). На рис. 13.3 иллюстрируется конкретная реализация этой абстрактной идеи.

Предположим, что сначала имеется поверхность тора (баранки), в которую вложена одномерная сфера (окружность) — она выделена на рис. 13.3. Теперь представим, что с течением времени эта окружность стягивается, и структура пространства рвется. Можно восстановить пространство," позволив ему разорваться лишь на мгновение и заменив сжатую одномерную сферу (стянутую окружность) нульмерной сферой — двумя точками, затыкающими отверстия в верхней и нижней части образовавшейся после разрыва фигуры. Как показано на рис. 13.3, в результате получится фигура, похожая на кривой банан, которую затем можно постепенно и гладко (без разрывов пространства) продеформировать в поверхность надувного мяча. В итоге мы видим, что при коллапсе одномерной сферы и замещении ее нульмерной топология исходного тора, т. е. его фундаментальная форма, радикально изменяется. В контексте свернутых пространственных измерений эволюция с разрывом пространства, изображенная на рис. 13.3, привела бы вселенную, показанную на рис. 8.8, к виду на рис. 8.7.

Рис. 13.3. Окружность в обхвате баранки (тора) коллапсирует в точку. Поверхность рвется, и образуются два прокола. В них «вклеивается» нульмерная сфера (две точки), которая замещает исходную одномерную сферу (окружность) и восстанавливает порванную поверхность. При этом становится возможным преобразование в фигуру совершенно иной формы — надувной мяч

И хотя все это лишь аналогия с меньшим числом измерений, здесь улавливаются основные идеи нашей с Моррисоном гипотезы о втором этапе, продолжающем исследования Строминджера. Нам казалось, что после коллапса трехмерной сферы внутри пространства Калаби—Яу пространство должно разорваться, а затем само собой восстановиться путем отращивания двумерной сферы, приводя к гораздо более серьезным изменениям топологии, чем те, которые Виттен и мы обнаружили в наших предыдущих работах (см. главу 11). При этом одно многообразие Калаби—Яу может, по существу, превратиться в совершенно иное многообразие Калаби—Яу (подобно тому, как тор превратился в сферу на рис. 13.3), но физические характеристики будут по-прежнему хорошо определены. Хотя картина начала вырисовываться, мы знали, что потребуется проработать некоторые важные моменты до того, как можно будет заявить о том, что на нашем втором этапе не возникают сингулярности, т. е. пагубные и неприемлемые для физики последствия. В тот вечер мы оба отправились домой в приподнятом настроении, ощущая близость нового важного результата.

Date: 2015-08-07; view: 303; Нарушение авторских прав