Фаза доказательства

Вернемся к примеру 1. Докажем формулу (*) методом математической индукции.

а) База индукции.

При n = 1 формула верна:

б) Индукционный переход.

Предположим, формула (*) верна для некоторого n = k, то есть

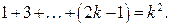
(1)

Докажем, что тогда формула (*) будет верна и для следующего числа , то есть

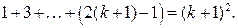
(2)

Записав сумму, стоящую в левой части формулы (2), как 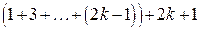, получаем, что (2) равносильно равенству

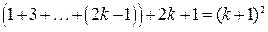
и вследствие индукционного предположения (1) равносильно также равенству

.

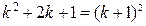Так как последнее равенство, очевидно, выполняется, значит, формула (2) также справедлива.

в) Вывод: формула (*) справедлива для всех n.

Пример 2. Рассмотрим числовую последовательность 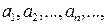которая строится следующим образом:

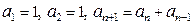для всех

(то есть каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов). Такая последовательность получила название «последовательность Фибоначчи», так как она связана с одной задачей, которую рассматривал итальянский математик Фибоначчи в начале XIII века (эта задача приводится в Приложении 2, поскольку имеет отношение к золотой пропорции).

Докажем методом математической индукции, что для этой последовательности справедлива формула

(**)

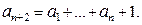
а) База индукции.

При n = 1 формула (**) запишется так:

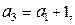то есть .

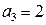Воспользуемся определением последовательности Фибоначчи:

.

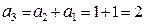Следовательно, при n = 1 формула (**) верна.

б) Индукционный переход.

Предположим, формула (**) верна для некоторого n = k, то есть

.

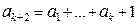(3)

Проверим, что тогда она будет верна и для следующего числа n = k + 1, то есть

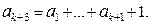
(4)

Сумму, стоящую в правой части равенства (4), можно записать как

,

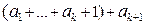следовательно, равенство (4) равносильно равенству

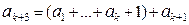
и вследствие индукционного предположения (3) равносильно также равенству

,

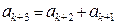которое выполняется по определению последовательности Фибоначчи.

Таким образом, мы доказали справедливость формулы (4) в предположении, что имеет место формула (3).

в) Вывод: формула (**) верна для всех n.

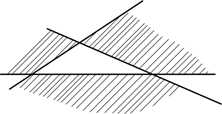
Пример 3. На плоскости проведено несколько прямых. Доказать следующее утверждение: области, на которые эти прямые разбивают плоскость, можно закрасить двумя цветами так, чтобы соседние области были закрашены различными цветами (см. рис. 3).

Доказательство. Пусть n – это количество прямых. Докажем методом математической индукции, что наше утверждение справедливо для всех n.

а) База индукции.

При n = 1 утверждение справедливо (см. рис. 4)

б) Индукционный переход.

Предположим, утверждение справедливо для k прямых. Теперь пусть имеется k +1 прямая на плоскости (см. рис 5а).

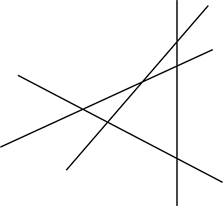
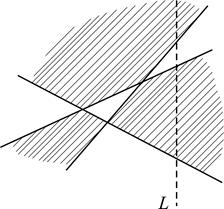
Рассмотрим наш чертеж без одной прямой (обозначим её L). Так как на плоскости остается k прямых, по индукционному предположению можно закрасить получившиеся области с выполнением нужного условия. Сделаем это (см. рис. 5б). Теперь рассмотрим чертеж вместе с прямой L. Для областей, находящихся по одну и ту же сторону от L, требуемое условие выполнено. Оно не будет выполнено только для тех областей, для которых общая сторона лежит на прямой L. Поменяем цвета на противоположные в тех областях, которые лежат по одну фиксированную сторону от прямой L (см. рис. 6).

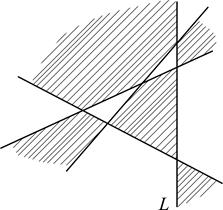
Тогда требуемое условие будет выполнено для всех областей. Таким образом, утверждение справедливо для k + 1 прямой.

в) Вывод: утверждение справедливо для любого количества прямых на плоскости.

Приведем еще один пример, в котором заведомо ложное утверждение «доказывается» методом математической индукции. (Разоблачение этого «доказательства» предоставляем читателю.)

Пример 4. Найти ошибку в доказательстве утверждения «Все лошади – одной масти».

«Доказательство».

Достаточно доказать, что для любого n справедливо следующее утверждение: «В табуне, состоящем из n лошадей, все лошади имеют одинаковую масть». Используем метод математической индукции.

а) База индукции.

При n = 1 утверждение, очевидно, справедливо.

б) Индукционный переход.

Предположим, утверждение верно для некоторого n = k, то есть любые k лошадей имеют одинаковую масть. Рассмотрим табун из n = k + 1 лошади. Пронумеруем лошадей от 1 до k + 1. По индукционному предположению первые k лошадей – одной масти, и последние k лошадей – одной масти (см. рис. 7).

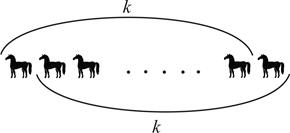
Следовательно, последняя лошадь – той же масти, что и остальные. Значит, в табуне из k + 1 лошади все лошади имеют одинаковую масть.

в) Вывод: «Все лошади – одной масти».