Алгебраический метод определения симметричных колебаний

Пусть нелинейная система, изображенная на рис. 2.2, имеет 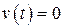и передаточную функцию линейной части . Полагаем, что выполняется гипотеза фильтра, т.е. АЧХ является фильтром низких частот, а нелинейность нечетно-симметричной, т.е. 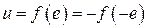. В этом случае имеем следующую модель системы:

, , .

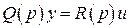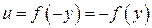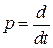Уравнение замкнутой системы будет

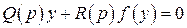. (2.57)

Полагаем, что нелинейное уравнение (2.57) имеет решени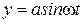е , где 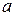, следует определить. После гармонической линеаризации

,

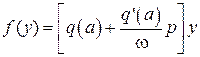так что с учетом этого уравнение (2.57) будет

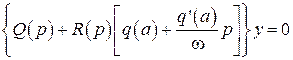. (2.58)

Уравнение (2.58) является гармонически линеаризованным уравнением замкнутой системы. Это линейное дифференциальное уравнение, коэффициенты которого зависят от двух постоянных 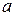и 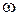− параметров искомого гармонического режима 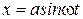, оно справедливо только для решений подобно типа.

Характеристическое уравнение замкнутой системы будет

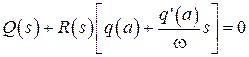. (2.59)

Линейное дифференциальное уравнение имеет гармоническое решение вида 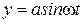только в том случае, если его характеристическое уравнение содержит пару чисто мнимых корней 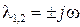, т.е. подставляя в (2.59) 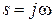, получим условие существования гармонического решения

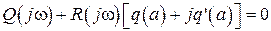. (2.60)

Выделяя в (2.60) действительную 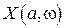и мнимую 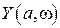части, и приравнивая их к нулю, получим условия существования периодического решения

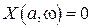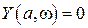, . (2.61)

Уравнения (2.61) представляют собой систему двух алгебраических уравнений с двумя неизвестными 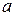, 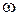и могут не иметь решения − периодический режим вида 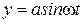не существует, иметь единственное решение, что соответствует существованию единственного периодического решения с амплитудой 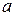и частотой 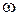, и, наконец, иметь несколько решений (возможно бесчисленное множество).

Полагая периодический режим с найденными амплитудой 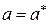и частотой 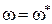существующим, рассмотрим вопрос об устойчивости этого режима. Предполагается приближенный способ оценки устойчивости периодического режима. Найдем для функци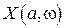й и 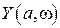частные производные по 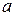и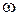

, ,

, .

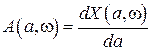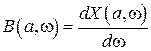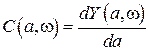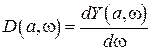В полученных выражениях положим 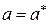, , 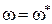тогда получим

, , , .

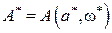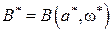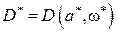Периодический режим с параметрами 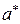, будет устойчивым, если выполняется неравенство

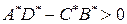(2.62)

при условии, что для коэффициентов многочлена

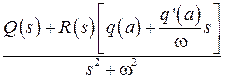(2.63)

выполняется условие критерия Гурвица [7].

Если найденный периодический режим устойчив, то в системе существуют автоколебания гармонической формы с параметрами 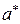, 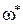. если неустойчив, то автоколебаний нет, хотя периодический режим существует.

Предложенный подход можно применить и для анализа несимметричных колебаний. При этом вместо системы двух уравнений (2.61) получим систему из трех уравнений для определения параметров , , .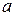

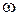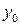Пример 2.4. Пусть в нелинейной САУ рис. 2.2 нелинейный элемент − идеальное реле с характеристикой 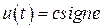, а передаточная функция линейной части имеет вид

.

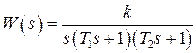Для нелинейного элемента имеем 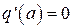, а 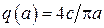(2.55). Уравнение (2.60) имеет вид

,

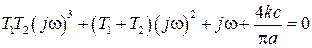из которого получаем уравнения (2.61)

, .

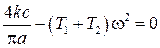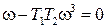Решая полученные уравнения, найдем амплитуду и частоту периодического режима:

, .

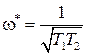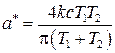Нетрудно проверить, что для найденных 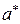, , 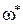условия (2.62), (2.63) выполняются, т.е. в системе возникают автоколебания и

.

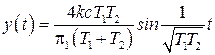Date: 2015-08-06; view: 562; Нарушение авторских прав