Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Определение поперечных сил и изгибающих моментов - сечение 1
|
|
Примеры
Построение эпюр Q и M для консольной и двухопорной балки
При составлении уравнений равновесия отсеченных частей балки, правило знаков для внешних нагрузок (например сосредоточенной силы F) определяется аналогично.
Другими словами, внешние силы и распределенные нагрузки, стремящиеся повернуть отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки считаются положительными, и наоборот.
Внутренний изгибающий момент M принимается положительным (т.е. M>0), если он стремится сжать верхние слои отсеченной части балки на рассматриваемом участке.
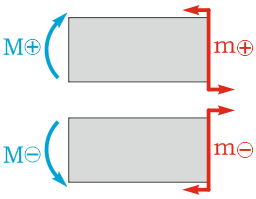
Правило знаков для изгибающего момента
Для внешних сосредоточенных моментов и моментов сил правило знаков аналогично, т.е. положительными считаются внешние моменты, сосредоточенные силы и распределенные нагрузки, сжимающие верхние слои балки.
5-6
ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
Определение поперечных сил и изгибающих моментов - сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой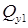 
и изгибающим моментом 
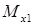. Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
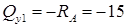кН.
Знак «минус» нами взят потому, что сила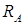 
вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
Видим два усилия: реакцию опоры и момент M. Однако у силы плечо практически равно нулю. Поэтому изгибающий момент равен:
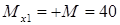кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Date: 2015-08-06; view: 567; Нарушение авторских прав