
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнение теплопроводности
|
|
Разностные методы решения дифференциальных
Уравнений в частных производных.
Одним из методов решения дифференциальных уравнений в частных производных является метод сеток.
Уравнение теплопроводности.
Рассмотрим задачу нахождения непрерывной на замкнутом прямоугольнике D={0£x£ l, 0£y£Y} функции u(x, y), удовлетворяющей уравнению теплопроводности
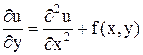 , (*)
, (*)
если заданы начальные условия:
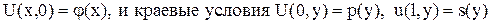 ,
,
где f(x, y), j(x), p(y), s(y) –заданные, функции (n раз дифференц.) такие что
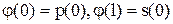 .
.
Поставленная задача называется смешанной, поскольку содержит как начальное, так и краевые условия.
Идея метода заключается в следующем.
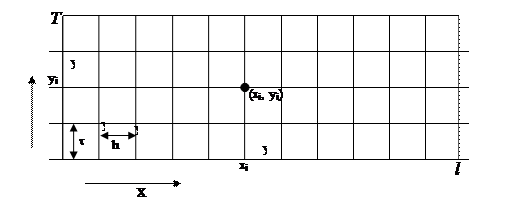
Разобьём отрезки [0, l] оси х и [0; T] оси у соответственно на n и n1 равных частей и введём обозначения: 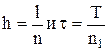 . Через точки деления проведём прямые, параллельные соответствующим осям. В результате область D разобьётся на прямоугольники с вершинами (хi, yi), где xi=(i-1)h, i=1,n+1, уi=(j-1)×t, i=1,n1+1.
. Через точки деления проведём прямые, параллельные соответствующим осям. В результате область D разобьётся на прямоугольники с вершинами (хi, yi), где xi=(i-1)h, i=1,n+1, уi=(j-1)×t, i=1,n1+1.
Множество вершин прямоугольников называется сеткой, а отдельные вершины – узлами сетки. Узлы, имеющие одинаковый индекс j, образуют j слой. Числа h и t называют шагами сетки соответственно по переменным х и у.
 |
y
По определению частная производная равна
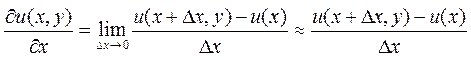
Если рассматривать функцию только в узлах сетки, то частную производную можно записать в форме
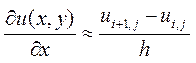
где узел 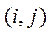 соответствует точке
соответствует точке 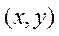 .
.
Полученное выражение называется правой конечной разностью. Название связано с тем, что для вычисления производной в точке используются значение функции в этой точке и точке, лежащей правее. Очевидно, что сходное выражение можно было бы получить, используя точку, лежащую слева.
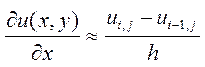
Такое выражение называется левой конечной разностью. Можно получить центральную конечную разность, найдя среднее этих выражений.
Теперь получим выражения для вторых производных.
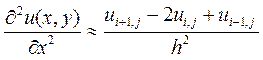
В данном случае для нахождения производной мы использовали симметричные точки. Однако, очевидно, можно было бы использовать точки с несимметричным расположением.
Заменяя производные, входящие в уравнение (*) разностными отношениями, получим конечно-разностные уравнения
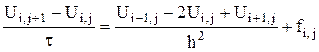 (**)
(**)
либо
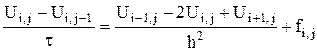 . (***)
. (***)
Эти уравнения аппроксимируют исходное дифференциальное уравнение в узле сетки (хi, уi) с погрешностью порядка О(h2+t).
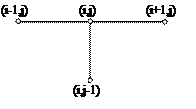 Для получения первого уравнения была использована конфигурация узлов (1), а для второго (2).
Для получения первого уравнения была использована конфигурация узлов (1), а для второго (2).
 |
Начальные и граничные условия определяют значения сеточной функции в граничных узлах:
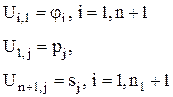
Тогда во внутренних точках сетки решение можно искать в явном виде по схеме (из уравнения (**)
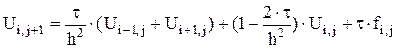
Date: 2015-08-06; view: 588; Нарушение авторских прав