материю и энергию

Такие элементы нашей многомерной природы являются сильными влияниями, способными “запускать” компоненты самоорганизации, свойственные биополю и другим тонкополевым структурам. В этом процессе происходит передача активной информации. Запуская процессы самоорганизации, мы воздействуем на динамическую область нашего “целостного” существа, идя от физического к духовному! Воздействие на часть воздействует и на целое. Существующий в наших энергетических полях голографический вид взаимосвязи обеспечивает то, что все энергетические системы могут быть настроены на новое состояние “баланса”, даже если работают с какой-то одной энергетической системой!

ОПРЕДЕЛЕНИЕ СТРУКТУРЫ РЕАЛЬНОСТИ

Чтобы расширить взгляд на самоорганизацию, мы сформулируем более общий вопрос: “Что такое структура физической реальности?” Алекс Кайварайнен разработал исчерпывающую общую модель физической реальности и сознания. В ней присутствует динамическое слоирование, или иерархия, связывающая реальность на различных уровнях. Также, в этой модели существует голографический вид наложения вибрирующих волн. В основе процесса самоорганизации лежат вибрационные режимы. Каждый последующий уровень реальности разворачивается из или относится к более упорядоченному вибрационному состоянию.

На вибрационные состояния могут воздействовать внешние влияния, такие, как космическое излучение или электромагнитное поле [8]. Согласно Кайварайнену, любой вид системы обладает способностью самоорганизации и эволюции.

Фактически, “...от атомов до живых организмов, галактик и Вселенной, (такие системы) склонны к состояниям Скрытой Гармонии, к реализации Золотого Сечения” [9].

Примеры отношения Золотого Сечения приводятся в учении Священной Геометрии [10]. Природа управляется фундаментальными, универсальными, простыми, но изящными формулами выражения!

МЕЖПРОСТРАНСТВЕННЫЙ ПРОЦЕСС

В книге Межпространственная физика, Рут описывает энергетический поток из более высоких энергетических полей как силу, восстанавливающую наш межпространственный космос [11].

Межпространственный вихрь соединяет физическую реальность с невидимыми источниками нашей Вселенной, и выше.

Подобная “вихревая” структура приложима и к физическому человеку. С ее помощью, он “межпространственно” связан со своим высшим сознанием. Такая связь служит руководством организации энергии и материи, посредством вида иерархической системы.

Невидимые энергетические силы, проходящие через вихрь из высшей реальности, несомненно, учитываются для наблюдаемых явлений самоорганизации различных “низших” систем. Мы можем рассматривать такой вихрь слоированным как кожица лука - серия торов, один в другом, где каждый слой соединен со следующим. В состояниях более высокого измерения происходят преобразования, которые в конце концов “нисходят” в материю.

СОЗНАНИЕ УПРАВЛЯЕТ САМООРГАНИЗАЦИЕЙ

Джек Сарфатти знакомит нас с идеей, что самоорганизация связана с сознанием. Она – результат деятельности поля разума (сознания), взаимодействующего с материей в процессе, который он определил как обратное действие [12]. Фактически, это Намерение разума, действующее на квантовом уровне материи. Существует двусторонняя петля обратной связи, соединяющая разум и материю; это приводит к спонтанной самоорганизации системы. Благодаря такой петле, на самом высоком уровне существует контролирующая структура, которая работает, так сказать, “мгновение за мгновением”, и управляет всеми творческими процессами.

В этой парадигме, Разум, Сознание и НАМЕРЕНИЕ неотделимы от физической реальности. Мы обладаем действием сознания, обеспечивающим геометрическую форму (процесс в - форме), которая организовывает и материю и энергию. Процесс самоорганизации становится активным процессом, в котором информация приобретает значение именно в организующей себя системе.

МНОГОМЕРНОЕ ИНТЕРАКТИВНОЕ ЯВЛЕНИЕ

Магнитное поле, Связанность и Настройка... таковы некоторые элементы, которые, по указанию Детелы, требуются для создания синтропических потоков на квантовом уровне. Когда эти условия удовлетворяются, происходит внутренняя самоорганизация. Делая это, система стремится к Скрытой Гармонии, определяемой более глубокоуровневыми математическими и геометрическими законами природы. Мы находим, что самоорганизующиеся системы управляются Сознанием, взаимодействующим с энергиями, которые перемещают межпространственный вихрь, связывая физический мир с более высокими уровнями реальности.

Во взаимоотношениях человека с человеком мы видим существование синтропических условий, способных влиять и запускать самоорганизацию энергетического поля другого человека. В этот процесс включаются магнитное и торсионное поля рук, несущих паттерны, предпочтительные направления и Намерение Сознания, взаимодействующее с энергетическими системами. Самоорганизация в любом аспекте энергетического поля человека выражается в реструктуризации энергетической системы как целого. Техника Балансировки ЭМП использует потенциал этих интерактивных эффектов.

Приложение В

Физическая модель биополя

Андрей Детела

Институт “Дж. Стефана”, Любляна, Словения

Впервые опубликовано в 1997 году – перепечатывается с разрешения автора

[Замечание читателю: см. книгу “ Магнитные узлы ” (стр. 269)]

РЕЗЮМЕ

Биополе (информационный и эволюционный компоненты)

Биологическая живая материя демонстрирует разнообразие тонких явлений, которые невозможно объяснить чисто биологическими процессами. Среди них, мы упоминаем информационные процессы (перенос, обработка и накопление информации) и эволюционные процессы в живых организмах (например, митоз и морфогенез). Такие явления могут быть лучше поняты посредством введения концепции биополя. Биополе – это тонкоматериальная структура, пронизывающая биологические клетки живых существ. Оно сильно отличается от мира атомов и молекул, но, однако, является частью того же материального мира и может быть объяснено в физических терминах.

Здесь, представлена теоретическая аргументация биополя. Предполагается, что биополе – это трехмерное паутинообразное полотно вибрирующих электрических и магнитных полей. Линии этого поля похожи на крошечные нити в трехмерной ткани. Такие электромагнитные поля демонстрируют очень сложную внутреннюю организацию.

Мы находим необычный вид киральных решений уравнений Максвелла, которые не рассеивают энергию и ведут к устойчивым полевым структурам. Они - так называемая информационная основа биополя. Самыми простыми структурами такого вида являются тороидальные узлы.

Когда электрический заряд очень маленькой массы входит в информационное биополе, происходят нелинейные явления. Такие нелинейные явления базируются на ветвлениях (бифуркациях) во внутренних электрических потоках и на эффектах резонанса между потоками и полями. Мы сталкиваемся с эволюцией полевой структуры. Эволюция – синтропический процесс, ориентированный во времени. Для синтропического поведения существует несколько очевидных условий, и одно из них – квантовая связанность в состояниях электрического заряда.

Биополе всегда содержит в себе как информационную основу, так и эволюционный компонент. Оба они необходимы. Первая подчиняется линейным уравнениям Максвелла и сохраняет структурную форму биополя. Линейность приводит к наложению многих различных нелокальных состояний, и, следовательно, к большей способности накопления информации. Второй отвечает за эволюцию биополя: от примитивных тороидальных узлов до очень сложных форм (со многими узлами), демонстрирующих все признаки жизни.

Структура биополя находится в тесном соответствии с молекулярной структурой живых организмов. Отдельные узлы в паутине биополя взаимодействуют с отдельными атомами и молекулами в живых клетках. Таким образом, биополе может регулировать множественные процессы в живых клетках. Самые возможные кандидаты для такого взаимодействия – киральные молекулярные структуры протеинов и нуклеотидов, например, микротрубки спиралей ДНК.

ВВЕДЕНИЕ

Многие информационные процессы и процессы самоорганизации внутри живых организмов могут быть лучше поняты и объяснены, если мы можем представить существование особых самоорганизующихся структур, полотна крошечных нитей высокочастотных электрических и магнитных полей. Нити переплетаются с молекулярными структурами в телах живых организмов. Концепция таких узловых структур не нова; она осознана многими старыми культурами. В классической Индии она называлась праной, в то время, как в современной научной традиции наиболее привычно использование выражения биополе. Биополе пропитывает всю живую материю, наше человеческое тело, животных, растения, грибы, бактерии, вирусы и частично даже кристаллы. Живя в симбиозе с протеиновыми структурами живых организмов, в живых организмах, биополе обеспечивает самоорганизацию для сохранения термодинамического состояния при самой низкой энтропии и для внутренних информационных взаимодействий. Теоретическое объяснение биополя – огромная проблема современной науки.

Чтобы получить некоторое основное понимание, кажется, что, по крайней мере, несколько новых шагов в новый необъяснимый мир должны быть сделаны одновременно. Особенно существенно понимание синтропических процессов в состоянии квантовой связанности. 1 Синтропическая природа биополя основана на возможном существовании электрически заряженных частиц очень маленькой массы и на особой пространственно-временной симметрии биополевой структуры. Здесь, асимметрия времени означает стрелу времени биополевых вибраций, в то время, как асимметрия пространства означает киральную биополевую структуру. В дальнейшем, мы будем детально разрабатывать эти два термина (см. раздел В).

Хотя до сих пор не существует прямых научных доказательств гипотезы биополя, она приобретает растущую поддержку, особенно в новой междисциплинарной сфере – стыке науки о познании, физики и биологии; границы между этими дисциплинами постепенно исчезают.

Биополе – это трехмерная (3-D) паутина c двумя основными функциональными качествами:

• Она способна хранить огромное количество информации (много бит

информации)

• Она способна к своей собственной неотъемлемой эволюции (процесс

самоорганизации).

В этой статье я представлю гипотезу: фактически, биополе - это чередование двух различных компонентов: информационной и эволюционной структур. Обе они являются определенными материальными структурами со свойственными им математическими особенностями. Биополе возможно только тогда, когда переплетаются эти две структуры. Здесь, мы исследуем несколько таких особенностей.

А: ИНФОРМАЦИОННЫЙ КОМПОНЕНТ БИОПОЛЯ

Одним из признаков хорошей системы хранения памяти (например, чип памяти компьютера или память человека) является:

• Система должны быть способна хранить огромное количество информации. Если оно трактуется в квантовом смысле (как это обычно делается в прогрессивной кибернетике Винера), это означает огромное количество битов информации. Бит информации может определяться как самое маленькое различие (в любом материальном смысле), которое может быть распознано читателем информации.

Этот крошечный бит информации должен быть доступен таким образом, чтобы его можно было прочесть (или записать) без искажения или изменения остальной информации. Следовательно, между различными частями информации должна существовать разделимость.

Внутри компьютерного чипа или на поверхности диска, различные части информации разделены в пространстве; в то время, как в живых организмах разделимости, возможно, не существует в терминах пространства. Например, недавние исследования мозга2 и других живых информационных систем показывают, что функции разума алокальны (нелокальны). Если это так, и если взаимно разделенные порции информации хранятся в области одного и того же пространства, тогда, по отношению к биополю, ясно следующее: Компонент биополя, ответственный за хранение информации, должен выражаться линейными уравнениями. Только в этом случае разные порции информации могут храниться независимо, ибо только тогда существует вероятность наложения (совмещения, наслаивания) линейно независимых решений.

Каким видом линейных уравнений удобно описывать информационный компонент биополя?

Существует много доводов3, подтверждающих, что биополе основано на электромагнитных явлениях (или, по крайней мере, тесно с ними связано). Уравнения Максвелла для электромагнитного поля линейны. Давайте попытаемся найти такую структуру электромагнитного (ЭМ) поля, чтобы эта полевая структура оставалась временно устойчивой, а энергия поля не рассеивалась. Только тогда мы можем говорить о памяти, вложенной в полевую структуру. Также, нам бы хотелось, чтобы полевая структура была устойчива к пограничным условиям. Такие дистанционные границы должны иметь только пренебрежимо малое влияние. В упрощенном виде, мы можем представить ЭМ поле как “облако”, ассимптотически приближающееся к нулю во всех областях, удаленных от его центра. Если такое поле поместить в большую коробку, то на стенках коробки оно такое слабое, что не оказывает никакого значительного влияния на полевую структуру.

Такая полевая структура имеет вид устойчивого волнового пакета. Он не двигается в пространстве. Мы уже можем описывать его, используя уравнения Максвелла в пустоте. Легко показать, что решения вышеописанных уравнений Максвелла удовлетворяют следующему условию:

rot B = k • B (1)

где В – вектор плотности магнитного потока (на протяжении всей статьи векторные величины обозначаются жирным шрифтом), и k – некая скалярная константа. Сначала, давайте обратим внимание только на гармонический вид решений, то есть, на решения, описанные

Е = Е_о • е^iωt (для электрического поля)

В = В_о • е^i(ω+δ) (для магнитного поля)

Мы вставляем гармонический вид решений в первые два уравнения Максвелла для ЭМ поля в вакууме:

rot B = ε_оμ_о • ∂Е/∂t

rot E = -∂B/∂t

Давайте испытаем некий особый вид решений: вектор магнитного поля В в каждый момент и в каждом месте коллинеарен вектору электрического поля Е:

В = i ω • (ε_оμ_о/k) • E (2)

Такие решения удовлетворяют уравнению (1), но никаким другим уравнениям (полагая, что решения гармоничны). Коллинеарность векторов Е и В – очень важное качество информационного компонента биополя. А именно, оно очень отличается от природы обычного ЭМ поля в пустоте или в однородной субстанции, где вектор Е перпендикулярен вектору В. Важное следствие этой коллинеарности (по отношению к вектору Направления) будет обсуждаться позже.

Уравнение (2) также включает в себя воображаемую величину i, что означает, что магнитное поле сдвинуто по фазе (на π/2, то есть, на одну четверть цикла) относительно электрического поля. В момент, когда магнитное поле достигает максимума (или минимума), электрическое поле равно нулю, и наоборот. Энергия электрического поля переносится в и из энергии магнитного поля, в то время, как сумма обеих энергий остается постоянной. Это похоже на все другие идеальные колебания без затухания. Например, в простом механическом осцилляторе сумма кинетической и потенциальной (или упругой) энергии постоянна по отношению ко времени.

Давайте начнем с примера. Когда электрическое поле равно нулю, в этот момент существует только магнитная энергия. Магнитное поле обладает определенной структурой, которую мы исследуем позже. Через четверть цикла, мы получаем идентичную структуру в электрическом поле, еще через четверть цикла она снова преобразовывается в идентичную магнитную структуру (но полярность поля меняется на противоположную). Кривые, представляющие линии обоих полей, не меняются со временем (Я использую термин линия поля вместо силовой линии). Относительная интенсивность электрического и/или магнитного поля меняется. Оба поля колеблются между положительной и отрицательной амплитудой. Однако, направления поля не меняется. Качественная картина обоих полей (полевой структуры) сохраняет свою первоначальную форму. Это особый вид волнового пакета – он не перемещается со скоростью света, он статичен, и все время остается в одном и том же месте! Он сохраняет свою внутреннюю информацию (которая находится в полевой структуре). Поскольку стоячий волновой пакет подчиняется линейным уравнениям Максвелла, такие пакеты могут накладываться друг на друга. Мы будем называть волновой пакет, который не перемещается со скоростью света (и, следовательно, обладает остаточной массой), информационной паутиной.

Давайте на минуту прервемся: Граница между информационной паутиной и классическим фотоном четко не определена. На этих страницах описывается бездействующая информационная паутина, хотя она, также, может обладать компонентом скорости (и все же медленнее, чем скорость света). Чем больше ее скорость приближается к скорости света, тем больше она похожа на классический фотон.

Следуя обычным процедурам с дифференциальными уравнениями Максвелла, мы легко можем найти циклическую частоту информационной паутины:

k² = ε_оμ_о • ω², или более просто

ω = ck (3)

где с – скорость света в пустоте.

Также, мы хотим определить пространственную конфигурацию этих решений. Нас интересует форма магнитных и электрических линий (обе имеют одинаковую форму). Существует много классов решений, но, сначала, мы будем ограничиваться такими решениями, которые проще всех и не слишком чувствительны к пограничным условиям. Как уже упоминалось, такие решения должны демонстрировать фактор асимптоты. Такое поле можно визуализировать как прямую, бесконечно длинную веревку, составленную из торсионно закрученных линий поля (рис. 1)

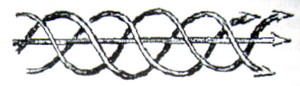Закручивание в центре веревки похо-же на правостороннюю спираль, если k>0, и на левостороннюю спираль, ес-ли k<0. Но наблюдение пограничных условий говорит, что решение относи-тельно цилиндрической системы ко-ординат не удовлетворительно. То есть, поле В не стремится к нулю, когда мы удаляемся в направлении z. Также, когда мы удаляемся в направлении r, оно не стремится к нулю достаточно быстро (результат потери асимптотического поведения). Полная магнитная энергия, которая может быть выражена пространственным интегралом ∫_v (2μ_о) • В² dV (интегрирование по всей области V), отклоняется, даже когда подсчитывается только магнитная энергия в веревке конечной длины.

Обе эти проблемы могут быть решены с помощью слегка измененной полевой структуры. Давайте представим, что вышеописанная веревка в поле имеет конечную длину (тогда мы имеем сегмент веревки) и скручена в виде замкнутой петли (рис. 2). В этом случае мы можем сразу же избежать первой проблемы. А как насчет второй? Несмотря на то, что благодаря новой модификации, в середине веревки поле меняется незначительно, оно может значительно измениться в области, удаленной от центра петли. Следовательно, можно ожидать абсолютно новых решений – возможно с конечной магнитной энергией.

Когда уравнение (1) анализируется в тороидальной системе координат4 ^{, 5}, могут быть найдены характеристики новых решений. Исчисления здесь очень сложные. Решения (тороидальные решения) не могут выражаться обычными аналитическими функциями. Но визуально, такие решения очень привлекательны. Они похожи на вышеупомянутые замкнутые петли, сделанные из спирально закрученных веревок. Таким образом, линии поля обладают той же самой структурой, что и нити тороидальных узлов6. Тороидальные узлы можно визуализировать как нить, намотанную на поверхность тора. Самый простой тороидальный узел показан на рисунке 3 (см. следующую страницу).

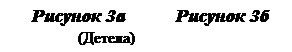
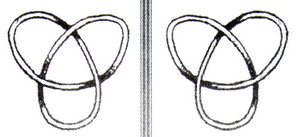Все тороидальные узлы киральны, то есть, имеют левосторонний и право-сторонний вариант. Киральные струк-туры – это такие структуры, у кото-рых отсутствует центр инверсии, это означает, что их зеркальное отраже-ние не идентично оригиналу. Таким образом, все киральные структуры яв-ляются двусимметричными формами, например, левая рука и правая рука (греческое слово kiros = рука), левосторонний и правосторонний шуруп, левосторонний и правосторонний узел (рисунки 3а и 3б), и так далее. Легко показать, что все математические решения уравнения (1) должны быть киральными: Дифференциальный оператор rot (= ротору) преобразовывает полярный вектор в аксиальный (осевой) (или наоборот), таким образом, k - это, фактически, не обычная скалярная константа – это псевдоскаляр7. Каждый псевдоскаляр обладает киральными свойствами. Когда константа k используется с противоположным знаком, мы получаем полностью эквивалентные решения, хотя и не идентичные – они являются зеркальным отражением оригинала.

Можно показать, что для тороидальных решений, вышеописанная область интеграла сходится. Тороидальные решения – хорошие решения для уравнения (1), ибо представляют собой нефиктивные полевые паутины, паутины с конечной энергией и нечувствительные к отдаленным пограничным условиям.

Здесь наблюдались только самые простые хорошие решения (тороидальные узлы), ибо они могут быть установлены умеренно простыми математическими инструментами. Также, для уравнения (1) могут существовать более сложные решения, например, заузленные структуры, не тороидальные и намного более сложные. Мы будем называть все эти заузленные структуры полевыми паутинами.

Легко видеть, что информационные паутины не излучают энергию. Вектор Направления8 выражается произведением векторов электрического и магнитного полей, но внутри информационной паутины, согласно уравнению (2), эти два поля полностью коллинеарны, и произведение их векторов обращается в нуль. Таким образом, в и вне этой паутины излучения не существует. В этом случае паутина временно устойчива.

Являются ли такие структуры устойчивыми к внешним возмущениям? Могут ли такие возмущения медленно искажать и разрушать наши паутины? Ответ на эти вопросы не прямой. Давайте оговорим две подсказки:

(1) Информационные паутины связаны с эволюционными паутинами (подробнее об этом позже). Синтропические процессы в эволюционных паутинах обеспечивают их устойчивость, и, в результате, также стабилизируют информационные паутины.

(2) Мы изучили уравнения Максвелла в классическом пределе, но в действительности, магнитный поток в паутинах квантованный. Если петли заузленной структуры очень крошечные и если плотность магнитного потока маленькая, то через каждую петлю проходит только очень ограниченное количество магнитного квантового потока (флюксонов). Паутина может излучать только тогда, когда значительное возмущение изменило бы поток, по крайней мере, на один флюксон.

Фактически, оба объяснения в основном означают одно и то же. Синтропическая природа материи – основа всех квантовых явлений. Сегодня мы все еще не можем говорить о детально разработанной теории квантовых процессов, интерпретированных посредством синтропической активности на субквантовом уровне (в субквантовом вакууме или, по другой терминологии, в эфире). Но некоторые, уже появившиеся предварительные концепции многообещающи. Такая интерпретация намного ближе к некоторым альтернативным интерпретациям квантовой физики (например, в современные времена к школе Бома), чем к уже существующей “классической” копенгагенской интерпретации.

Мы видели, что уравнение (1) приводит к крайне интересным решениям и ситуациям. Как иллюстрацию, позвольте упомянуть о другом интересном приложении того же самого уравнения. Если мы монтируем тороидальную катушку, следуя линиям, являющимся решениями уравнения (1), то электрический ток в такой катушке полностью коллинеарен вектору магнитного поля, генерируемого этой же катушкой. Такая катушка свободна от сил Лоренца, то есть, механически очень устойчива. Катушки такого типа иногда используются для генерирования очень сильных магнитных полей, если бы ограничивающим фактором9 могла быть механическая сила самой катушки.

В: ЭВОЛЮЦИОННЫЙ КОМПОНЕНТ БИОПОЛЯ

Здесь, ЭМ поле обладает структурой, похожей на информационные паутины (киральные узлы – по крайней мере, частично тороидальные узлы). При некоторых условиях, эволюционная паутина может перерастать информационную. Основное условие для этого – наличие в области паутины электрического заряда. До настоящего момента, мы обсуждали ЭМ поле в пустоте. Изотропная однородная субстанция не могла бы изменить наши уравнения (потребовалось бы только прибавить диэлектрическую константу с). Это было бы даже более реальным, ибо биополе редко обнаруживается отделенным от биологической материи. Однако, наличие электрического заряда высокой подвижности вносит критическую новизну в наши уравнения: этот заряд рассеивается преимущественно только в ЭМ поле паутинообразной структуры.

Если в паутине соблюдаются условия для синтропических процессов (см. ниже), в биополе начинается синтропическая самоорганизация. Это нечто большее, чем просто обычная самоорганизация протеиновых структур (autopoiesis10) или самоорганизация в рассеивающихся структурах11 Пригожина. Все три установленных явления (autopoiesis, самоорганизация Пригожина и синтропическая самоорганизация) происходят, когда материя далека от термодинамического равновесия. Это очевидно для всех трех процессов самоорганизации. Разница в том, что синтропические процессы (в отличии от двух других) сами создают состояние, далекое от термодинамического равновесия12. Первичное нарушение равновесия может вноситься колебанием, превышающим определенный порог. С этого момента, нарушение равновесия продолжается без какого-либо внешнего вмешательства.

Синтропические процессы, создающие новые эволюционные паутинообразные структуры, происходят при следующих условиях:

• наличие электрического заряда высокой подвижности

• низкая масса несущих заряд частиц

• киральная симметрия с паутинообразной структурой

• ориентированный во времени паттерн ЭМ вибрации (стрела времени в

паутинообразной структуре)

• квантовая связанность в состояниях заряженных частиц (длина

связанности превышает период заузленной структуры)

• адекватная амплитуда плотности магнитного поля.

Третье условие выполняется с самого начала, ибо структура информационного компонента уже киральная. И все же, четвертое условие (стрела времени) выполняется не автоматически. Однако, адекватное первичное колебание создает стрелу времени, и с этого момента, становятся возможными все последующие синтропические процессы самоорганизации. Немного позже мы будем описывать это колебание более детально. Наше описание будет основываться на современной теории хаоса.

Третье и четвертое условия представляют собой требуемые свойства пространственно-временной симметрии паутинообразной структуры. Они предписываются некоторыми основными физическими законами (неизменность единичных преобразований пространства и времени). В совершенном квантовом состоянии заряженной частицы должны быть отражены паттерны структуры с требуемой симметрией пространства-времени, но это возможно только тогда, когда длина связанности квантового состояния превышает, по крайней мере, размер отдельных узлов, а связанность времени – по крайней мере, один период ЭМ колебания. Этот факт приводит к пятому условию. Несомненно, квантовая связанность – чисто квантовый эффект и не обладает никакой классической аналогией13. Причина этому - особая информационная взаимосвязь в квантовых состояних; такая взаимосвязь не имеет места в классическом мире. Квантовая связанность вносит в физику совершенно новые понимания – давайте вспомним Аспекта и другие экперименты14, относящиеся к Восприятию Удаленных Электрических волн.

Второе и шестое условия взаимосвязаны: Необходимая амплитуда магнитного поля обладает некоей связанностью с массой заряженных частиц и с размером петель заузленной структуры. Чем больше масса и меньше размер петель, тем больше результирующее критическое поле (больше о критическом поле позже). Все это работало бы только с электронами, если бы петли были очень большими, но, как следствие, длина связанности тоже должна была быть большой. Такого рода эффект мог быть возможен в сверхпроводящих материалах. Температурное группирование сверхпроводящих пар Купера и атомов материи незначительно; следовательно, в этом случае происходила бы только самоорганизация электронного газа (без группирования с сетью). Несмотря на это, такой гипотетический процесс в сверхпроводниках предлагает невероятные возможности для обработки информации. Совсем не глупо предположить, что нечто похожее происходит в меланиновых белковых структурах нервной ткани (Коуп). Также мы можем себе представить многие другие виды квантовых компьютеров15 на том же самом уровне.

В этой статье, я буду обсуждать другой вариант процессов самоорганизации. Давайте представим существование электрически заряженных частиц с очень маленькой остаточной массой. Числовые прикидки подсказывают, что в этом случае синтропические условия легко выполнимы, даже если магнитное поле очень слабое и длина связанности относительно мала. Такие частицы ускользают от наших обычных наблюдений и измерений. Почему? Как я уже указывал в своих последних работах, такие частицы не могут существовать независимо, а только вместе с завершенной паутинообразной структурой. Их дом – паутина, возможно, она, также, и их тело – паутинообразная структура может определять их проявленные свойства (а вместе в этими свойствами и сами частицы). Также, паутинообразная структура препятствует аннигиляции (уничтожению) сверхлегких частиц и античастиц, храня каждый из этих видов в отдельных областях.

Таким образом, обнаружение сверхлегких частиц будет невозможно до тех пор, пока мы не научимся обнаруживать биополе (обнаружение научным методом). Паутины остаются в связанном самосохраняющем и самоорганизующем состоянии без внутреннего переноса энергии (вектор Направления для информационной компоненты равен нулю). Но, несмотря на это, существует некая внутренняя информационная взаимосвязь. Перенос энергии – не то же самое, что перенос информации (информация и энергия – не одно и то же)! Как только растворяется биополе, растворяются также и сверхлегкие частицы. Посредством аннигиляции и других реакций, они преобразуются в фотоны и другие известные частицы. Сверхлегкие заряженные частицы находятся в тесной связи с биополем; они создаются и уничтожаются вместе с ним. И, вместе с полем, они – паутина.

Следовательно, для полного понимания, существенно знать, что паутины одушевлены. С другой стороны, традиционная физика основана на передаче информации только в связи с передачей энергии (например, гамильтонианское представление влияний в квантовой механике). Она трактует материю как нечто мертвое, измеряет только мертвые частицы и, следовательно, сначала убивает паутины, а потом теряется возможность узнать о них нечто новое16.

Синтропический процесс, хранящий живую эволюционную паутину, - выразительно нелинейное явление. Эволюционная паутина (основанная на нелинейном синтропическом процессе) контролирует линейную информационную паутину. Как мы вскоре увидим, страведливо также и обратное: Линейная информационная паутина контролирует нелинейную эволюционную паутину. Эволюционный компонент биополя является той прибавкой к информационному компоненту, которая ведет к его эволюции. И в противоложном смысле, информационный компонент является первичной информацией (как первичное семя) для эволюционного компонента. Синтропический (эволюционный) процесс отличается только определенными пространственно-временными паттернами (топологиями) паутинообразной структуры. В таких синтропических областях мы не обнаруживаем никакой синтропической самоорганизации (например, если поле не превышает некоего критического поля). Следовательно, синтропический паттерн является аттрактором (точкой притяжения) (известным из теории динамики нелинейных систем), создающим себя в эволюционной паутине. Если паутинообразная структура очень проста (самые простые синтропические узлы, которые могут выжить), то аттрактор может быть периодическим, но в более сложных паутинообразных структурах мы обнаруживаем аттракторы, обладающие б о льшим сходством с хаотическими аттракторами. Однако, такая “хаотичная” природа проявляет особые черты, характерные только для синтропического поведения. (Например, аттракторы в рассеивающихся структурах Пригожина совсем другие.) Эволюционная паутина вибрирует и постоянно преобразовывает себя, согласно своим собственным природным законам. Следовательно, аттракторы такого вида можно отнести к особому классу: синтропическим аттракторам.

Почему информационная и эволюционная паутины так тесно связаны? Потому что киральная полевая структура эволюционных паутин очень похожа на киральную полевую структуру информационных паутин. Главная причина такого сходства в том, что обе паутины могут описываться одними и теми же дифференциальными уравнениями17. В следующих параграфах я буду представлять довод (хотя очень неточный), что уравнение (1), описывающее структуру информационной паутины, справедливо и для эволюционной паутины на ранних стадиях ее развития:

Траектории заряженных частиц внутри эволюционной паутины (взятые как среднее многих заряженных частиц) выравниваются вдоль линий магнитного поля этой же самой паутины:

j = f (B) (4)

где, j – вектор плотности электрического потока. Векторная функция f (B) нелинейна, плотность потока j может быть выражена экстремумами в определенных плотностях магнитного поля В. В таких случаях мы можем ожидать синтропическую ориентацию (направление) заряженных частиц.

Сейчас, давайте рассмотрим, что происходит, если функция (4) была бы линейной. Несомненно, такое допущение не имеет места в синтропической области параметров (когда плотность поля больше, чем критическая величина – как мы увидим это вскоре). Однако, мы заинтересованы в знании, где находится источник нелинейности (и синтропического направления). Мы начинаем с наблюдения ранней эволюционной стадии, когда поле В еще слабое (ниже критической величины), но уравнение (4) все еще справедливо. На этой стадии, линейный термин уравнения (4) предписывает:

j = p • B, где р – скалярная константа (снова псевдоскаляр). (5)

Когда j вставляется в первое уравнение Максвелла (сейчас, мы также имеем влияние материи и электрические потоки заряженных частиц), мы получаем:

rot B = εε_оμμ_о • ∂Е/∂t + μμ_о • В (6)

Давайте снова допустим, что вибрация гармонична и что векторные поля Е и В коллинеарны (что истинно для простых информационных паутин), тогда мы получаем уже известное уравнение

rot B = k' • B (7)

подтверждающее наше допущение о коллинеарности полей Е и В. Если бы два оставшихся допущения тоже были истинными (что функция f линейна и вибрация гармонична), то эволюционная паутина и соответствующая информационная паутина демонстрировали бы одну и ту же пространственно-временную структуру ЭМ поля (другим был бы только размер, а именно k ≠ k'). Но в синтропической области параметров не могут быть выполнены ни первое, ни второе условия. Функция j = f (B) должна прерываться, чтобы быть линейной выше критической точки, и вибрация больше не гармонична, если прибавляется временно-ориентированная эволюция. (Но она все еще может выражаться суммой гармонических вибраций формы Фурье.)

Эти две сложности (нелинейность и негармоничность) деформируют паутинообразную структуру и делают ее более запутанной. Как мы могли бы описать такую деформацию?

Во-первых, давайте рассмотрим негармоничность. Каждая периодическая вибрация (даже негармоничная) может быть выражена гармоническими компонентами Фурье. Уже существующие уравнения (по определению) линейны, таким образом, можно обнаружить отдельные решения для каждого гармонического компонента отдельно (как мы знаем, самые простые решения – киральные структуры в форме тороидальных узлов), затем, мы можем суммировать эти решения для отдельных гармонических компонентов. Следовательно, совокупное решение должно быть суммой, представленной различными узлами (разное k' для разных гармонических компонентов). Отношение между частотами гармоничных компонентов очень регулярно (отношение между разными числами), тогда уравнение (3) (вместе с допущением линейности) тоже создает регулярное отношение между параметрами k'. Это означает, что структура совокупного узла (сочетание всех гармоничных компонентов) тоже будет регулярной. Естественно, совокупный узел теперь намного более запутанный, чем тороидальный, и, более того, его совокупная топология меняется в течение одного периода (чего не происходит с узлом одного чистого гармонического компонента).

Но теперь, мы все еще имеем нелинейность функции (4). Это условие изменяет структуру узла еще более радикально. Чтобы упростить анализ, давайте начнем с паутины, состоящей из одного чистого гармонического компонента.

Нелинейная зависимость (4) может быть записана в форме потенциального ряда степеней (но без условия, что n = 0, ибо когда В = 0, j = 0 тоже; нет синтропического направления частиц).

j = ∑ р_n • Bⁿ (8)

n = 1,2,3…

Давайте понаблюдаем за условиями, когда В увеличивается от В = 0. Сначала В маленькое (например, в тороидальном узле). В более высоких полях линейная структура страдает от непрерывной деформации. Позже, в критическом поле В_k создается неустойчивость18, и узловая струк-тура страдает от резкого изменения (фазового превращения). При еще более высоком поле В, в дополнительную структурную разновидность вносится бифуркация. Хотя такие бифуркации тоже являются видом фазового превращения, они обладают особым свойством; из первоначальной фазы не всегда развивается такая же новая фаза – существует несколько возможностей. Линия фазовых возможностей расщепляется с каждой бифуркацией. Магнитный узел еще больше усложняется, хотя внутренне упорядочен не меньше (рисунок 4). Подобные явления известны из неравновесной 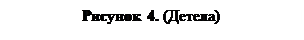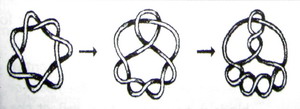термодинамики рассеивающихся систем (например, хорошо известные клетки Бенарда в турбулентной жидкости). Однако, существует и основное отличие: Синтропические структуры не нуждаются в подпитке из окружения (например, в подпитке температурными различиями, как в случае клеток Бенарда, или посредством некоторых других градиентов).

Что происходит с нашей первоначальной паутиной? Благодаря синтропическому направлению электрического заряда в паутине, к первоначальному информационному компоненту прибавляются увеличивающиеся величины эволюционного компонента биополя. Давайте подробнее рассмотрим, где происходит зарождение синтропии. Синтропия основана на бифуркациях в электрических потоках внутри паутин. Бифуркация происходит тогда, когда поле, растущее из информационного поля, превышает последующие критические величины. Бифуркации всегда демонстрируют гистерезисы (оставания фаз, запаздывания), следовательно, являются необратимым явлением. Когда поле возвращается к своей нулевой величине, паутина не проходит через те же самые фазы, как когда поле росло с нуля. Следовательно, мы получаем ориентированную во времени вибрацию – необходимое условие для синтропии. Из чисто гармонического колебания, мы получаем ориентированную во времени смесь гармонических вибраций, из примитивного пространства (которое не могло быть представлено даже одной буквой алфавита) мы получаем сложную структуру (которая должна быть представлена длиной целого слова). Здесь происходит эволюция “слов”. Некоторые из них расплывчаты (их энергия поглощается более сильными словами). Но другие выживают, особенно те, которые удовлетворяют уравнению (1), потому что такие структуры не рассеивают свою энергию. (Однако, параметр k', относящийся к плотности узла, сейчас, вероятно, выше). Итак, мы видим, что эволюционный компонент так же контролирует информационный, как информационный компонент определяет эволюционный. Таким образом, круг замыкается.

Описанный процесс ориентирован во времени. Тогда можно ли ожидать, что энергия поля рассеивается (в тепле), как в других необратимых процессах? Нет, рассеивания не происходит. Потому что простая эволюционная паутина состоит только из ЭМ поля и заряженных частиц. Энтропия заряженных частиц не может расти, если уравнение (4) описывает любой процесс направления частиц, и если направление действует на частицы с полностью расплывчатым или хаотическим движением. Немного позже я буду использовать термин эфир – термин, который может быть понят намного легче на востоке (например, даосистом), чем западным способом мышления. Сейчас, существенно, что эфир, даже в своем основном квантовом состоянии (состояние с самой низкой энергией), обладает моментом расплывчатости, и уравнение (4) к этому чувствительно. Но, может ли быть так, что энтропия ЭМ поля увеличивается? Если поле содержит только информационный компонент, то, несомненно, что энтропия не увеличивается. Такое информационное поле – основа, на которой растет эволюционный компонент. Одна часть паутинообразной структуры (одна часть узлов) относится к растущей энтропии эволюционного компонента; эта часть быстро разрушается. Другая часть относится к уменьшению энтропии или, другими словами, к росту синтропии; эта часть выживает и продолжает свою эволюцию. Следовательно, общая энтропия паутины не растет. Здесь, идея энтропии становится минимально важной, ибо классическая термодинамика (с ее вторым законом) больше не имеет силы. Рост синтропии (а не рост энтропии19^, 20) вносит в природу направление времени, и возникает необратимость. Синтропия имеет дело с эволюцией паутин (эволюция букв в слова, которые превращаются в еще более зрелые слова...). Эволюцию также можно трактовать с помощью теории информации. Посредством эволюции, количество битов информации растет. Эволюция – явление системное, и известно в современной микробиологии. Б о льшая часть развившихся паутин выживает, остальные разрушаются и сразу же поглощаются выжившими. Направление времени происходит в направлении роста внутренней информации, в направлении познания, в направлении (само)организации материальных структур.

Другое огромное преимущество разнообразия нелинейных синтропических структур скрыто в том факте, что каждый минутный период вибрации биополя (порядка 10^-15 для биополя с частотой солнечного света – больше об этом в следующей главе) представляет собой один полный эволюционный цикл: Когда, после одного колебания, поле В снова достигает своей амплитуды, его структура не такая, какой была первоначально. Возможно, мы начинали с простого тороидального узла, но сейчас у нас есть полный пучок из десяти взаимодействующих узлов. Новая структура является семенем для следующего периода, когда она становится еще более разнообразной. Мы знаем нечто похожее из цикла жизни растений. Каждую осень рассеиваются новые семена, чтобы дать возможность новой жизни в следующем году.

Описанная до сего момента теория включает в себя гипотетическое существование сверхлегких заряженных частиц. Возможно, сами по себе эти частицы на обладают никакой определенной формой; и только синтропическое включение в паутины определяет их квантовые особенности. Я использую термин эфир для непроявленной совокупности этих частиц, ибо такое название (описывающее явления такого типа) долго использовалось в европейской донаучной литературе. С другой стороны, санскритское слово прана больше подходит для уже упорядоченных синтропических структур, и, следовательно, относится к эфиру, который, предполагается уже проявленной формой.

Наше обсуждение эволюционного компонента биополя не так математически строго по сравнению с обсуждением информационного компонента. Все, что нам требовалось для информационного компонента, это уравнения Максвелла в пустоте, в то время, как в случае эволюционного компонента все не так просто. Нам пришлось прибегнуть к нескольким допущениям; я буду защищать их позже, когда позволят время и пространство. О самом эфире следует сказать намного больше – в конце концов, что это? Тогда, вот синтропические состояния и синтропия. Следует сказать больше и о взаимоотношении паутин с квантовым состоянием, о квантовой связанности и так далее. Ответы на эти вопросы частично взаимосвязаны. Прошу прощения, что в данный момент не могу войти в эту крайне широкую область со всем требующимся осознанием и концентрацией.

С: ОБА КОМПОНЕНТА БИОПОЛЯ СВЯЗАНЫ ВМЕСТЕ

Явления биополя лучше понимаются только тогда, когда мы рассматриваем оба компонента вместе – информационный и эволюционный компоненты. Биополе – это всегда симбиоз их обоих. В биополе с очень сложной паутинообразной структурой, мы даже можем ожидать специализацию в конкретных областях, следовательно, мы находим преимущественно информационные или преимущественно эволюционные области.

Если бы не было информационного компонента, эволюция биополя выродилась бы очень быстро. Затем, развивались бы очень хаотические структуры (весьма далекие от тех, которые могут описываться периодическими аттракторами). Возможно, основа для квантовой связанности вскоре стала бы разрушаться, и, таким образом, синтропия и эволюция в биополе умерли бы. Более того, на примере простого случая (обсуждаемого позже), мы увидим, что каждое устойчивое биополе на внешнем конце должно быть замкнуто в оболочку, которая состоит преимущественно из информационного компонента.

Также существеннен и эволюционный компонент. Без него биополе не могло бы осуществлять одновременные ремонты многих мелких дефектов в паутинообразной структуре. (А именно, когда биополе взаимодействует с окружением, возмущения вызывают энтропическую деградацию.) Более того, биополе без эволюционного компонента всегда оставалось бы в примитивном состоянии развития, со структурой самых простых тороидальных узлов.

Мы может представлять, что магнитное поле В внутри паутинообразной структуры существующего биополя выглядит следующим образом: Первая часть (информационный компонент) соответствует линейным уравнениям (1) для информационных паутин. Линейная часть паутинообразной структуры не излучает никакой энергии. Такая структура хранит себя. Это как прочная поддержка, благодаря которой, в каждый период нового колебания, прибавляет себя вторая часть биополя (эволюционный компонент). Благодаря нелинейным эффектам (уравнение 4), общее реальное поле паутины немного отличается от чисто информационного компонента. Давайте назовем это различие (между реальным и чисто информационным полем) нелинейным излишком биополя. Вообще говоря, вектор Направления этого излишка должен быть нулевым (векторы Е и В больше не коллинеарны). А именно, в нелинейной части истинны более сложные взаимосвязи, чем выражаемые уравнением (5); также, уравнения (6) и (7) справедливы только приблизительно. Для паутинообразной структуры строгие решения отличаются от решений, определенных уравнением (1). Колеблющиеся уровни излучения между различными областями паутинообразной структуры присутствуют в эволюционном компоненте. Энергия двигается, и структуры непрерывно изменяют свою форму. Однако, синтропия жива только при параметрах поля, замкнутых в строго ограниченных интервалах величины: в частности (как уже упоминалось), плотность потока j (уравнение 4) имеет хорошо обозначенные экстремумы только при определенных величинах плотности поля, плотности узлов и так далее. В этом случае, бифуркации не могут развиваться выше определенной степени, что накладывает ограничения на синтропическое поведение. Эволюция стянута в области динамической устойчивости.

Как следствие, за один период колебания все биополе изменяется ненамного. Биополевой аттрактор почти периодичен, особенно если мы рассматриваем только ограниченную область пространства. Особый вид видимой хаотичности (хаотичности в терминах современных теорий хаоса) очевиден только в наблюдених больших областей пространства-времени. Но такая хаотичность очень отличается от той, которая наблюдается в случае несинтропических аттракторов. Однако, слово хаос – не очень удобный для использования здесь термин, из-за его греческого происхождения; это слово означает неразбериху, беспорядок (нечто негативное в человеческом смысле). Но синтропический танец природы - нечто совсем другое. Он превосходит концепцию беспорядка уже с самого первого движения.

Информационная часть тоже все время не остается неизменной. На нее тоже влияет эволюция, ибо уравнение (1), верное для информационного компонента, приблизительно справедливо и для всего биополя, вместе с нелинейным (эволюционным) излишком. Но, посредством эволюции, биополе быстро создает такие структуры, которые стремятся сохранять энергию и информацию так, чтобы ограничивать рассеивание. В этом больше всего заинтересовано биополе. Биополе, не способное хранить свои собственные информационные паттерны, быстро исчезает. Остается только то, которое выражает правильное отношение к своей собственной внутренней информации. Несомненно, все эти концепции известны из биологии и микробиологии (обнаружения жизненных паттернов индивидуальных клеток или даже более мелких структур живой материи).

Итак, выживает только биополе с очень определенной внутренней пространственно-временной топологической структурой. Это выражается в действии строго определенных пространственных паттернов нитей в трехмерной “ткани” биополя или посредством строго определенной согласованности временных ритмов этих нитей. Такое биополе может быть результатом долгой эволюции, которая совсем не короче, чем эволюция молекулярной стороны живых организмов. Также, вероятно, что, благодаря биополю, эволюционировали отдельные органы (или органеллы), и они существуют для очень конкретных функций: Информационные линии (от отдельных нитей биополя), похожие на вид “нервной системы”; практически не эволюционирующие области, как вид памяти; механизмы очистки нежелательных форм биополя и так далее. Очень возможно, что эти функции, по крайней мере, частично прибавляются к соответствующим функциям в молекулярном живом мире – это придает биополю б о льшую устойчивость. От такого симбиоза получают взаимную пользу и биополе, и молекулярные структуры живых организмов. Именно поэтому большая часть биополя, как только оно сплетается из солнечного света, переплетает себя с протеиновыми структурами живых организмов.

Один короткий вопрос: Как из солнечного света плетется биополе? Наиболее вероятный сценарий следующий: Фотоны от Солнца рассеиваются протеиновыми структурами зеленых растений. Все протеины киральны, и, следовательно, оптически активны. Вероятность поглощения обоих циркулярно поляризованных компонентов другая, когда фотон рассевается на оптически активную молекулу (циркулярный дихронизм или эффект Коттона)21. Таким образом, создаются циркулярно поляризованные фотоны. Также, фотоны обладают киральной симметрией. Возможно, биополе даже обладает особыми органеллами, посредством которых фотоны могут лучше замедляться, захватываться и внедряться в биополевую структуру. (Это было бы аналогией со щупальцами, ртом, горлом и желудком каракатицы.) Ранней весной (для пояса умеренного климата это март), когда биополе деревьев еще слабое, протеины в коре должны переносить большую часть своей активности на более позднее время. Но позже эти процессы облегчаются: Протеины зеленых листьев объединяются и, в результате, больше сотрудничают с биополем.

Наиболее вероятно, что именно целостность биополя синхронизирует колебания вновь образовавшихся паутин, посредством ориентированной во времени настройкой существующего биополя. Ориентированная во времени вибрация становится значительно более сложной, поскольку приобретает все больше и больше информации о существующем биополе и о будущих перспективах биополей. Такая настройка – сказочник и мечтатель, носитель эволюции, самочувствующая жизненная цель, пропитывающая поры всех живых организмов.

Какой вид интуиции вел Луи Пастера, когда 150 лет назад он приписал стремление к жизни (жизнедающую силу и способность к саморганизации) именно киральным молекулам?

Благодаря динамическому равновесию между излучением от Солнца и возвращающимся в космос инфракрасным излучением, термодинамическая температура поверхности Земли приблизительно 300˚К. Но биополе не стремится к такому же равновесию, ибо может сохранять излучение внутри себя (такова сама природа биополя). Фотоны от Солнца захватываются биополем без каких-либо резко выраженных процессов (благодаря самоорганизующейся природе биополя), поэтому его температура уменьшается незначительно. Таким образом, температура биополя приблизительно такая же (или может быть даже выше), как на поверхности Солнца (6000˚К). Но в действительности, здесь трудно говорить о температуре. Термодинамическая температура может определяться только в сфере действия второго закона (Закона Энтропии). Когда синтропические процессы живые, разные пространственные области биополя могут иметь очень разные “температуры”. При возникновении бифуркаций в эфире, увеличиваются плотность узлов и частота (выше гармонических компонентов), а также поднимается “температура”.

Тем не менее, нам бы хотелось знать приблизительную энергию одного узла биополя. Единичный фотон от Солнца обладает энергией около 2-3 еV (4.10^-19J). Таким образом, один узел обладает остаточной массой около 4.10^-36кг (4.10^-6 массы электрона). Масса образующих эфир заряженных частиц может быть приблизительно такой же, при допущении, что фотон порождает эти частицы. Возможно, такие заряженные частицы даже идентичны некоторым узлам (в этом случае, узлы либо заряжены, либо нейтральны).

Классический радиус заряженной частицы с вышеуказанной энергией около 0.6 нм (при допущении, что заряженные частицы несут одну единицу заряда). Это для показателя 2π • 137 (связанного с тонкой структурной константой ∞) и меньше, чем длина волны фотона с соответствующей энергией. Это могло бы означать, что до некоторой степени, синтропические процессы все еще способны вплетать филигранные детали в первичную информационную паутину. Такое сложное плетение может происходить на уровне индивидуальных атомов приблизительно такого же размера (несколько десятков нанометров).

Чтобы видеть все яснее, давайте посмотрим на самую маленькую область биополя, которая может сохранять синтропические функции; мы будем называть ее клеткой биополя. Внутри мы обнаружим эволюционные области, взаимодействующие с информационными нитями – они сохраняют требующуюся устойчивость. Но внешняя оболочка (почти) полностью удалена от информационного биополя так, чтобы энергия не утекала. Мы замечаем интересное сходство с биологической живой клеткой, имеющей внешнюю мембрану и внутреннюю протоплазму. Возможно, часто внутри также существует и информационное ядро (как в эукариотических [5] клетках)?

Сейчас, мы входим в чудесный новый мир, переплетенный с качеством жизни. Его законы существуют не только на уровне каталитических циклов в протеиновых структурах (как в случае молекулярной билогии), но и на уровне основных узлов биополевой паутинообразной структуры. Мы можем понять, почему биополе демонстрирует такую замечательную способность регулировать молекулярные процессы в наших телах; оно приспосабливается к ним очень легко. По сравнению с “неуклюжими” молекулами, оно обладает намного более лучшими возможностями самоорганизации, благодаря хранению и обработке информации. Мы видели, что биополевая структура значительно киральна, петли в узлах трехмерных синтропических паутин спиралевидны. Поэтому, биополе легче интегрирует себя в похожие киральные (спиралевидные) структуры протеинов или нуклеотидов. Две такие структуры с очень регулярной спиральностью являются двойными спиралями ДНК и спирально структурированными микротрубочками22^, 23. Оба вида биомолекул играют крайне важную роль в хранении и обработке информации в живых клетках.

Я благодарю Д-ра Марту Кланишек-Гунде, внесшую много предложений, и Митю Перус, кандидата наук, поощрявшего меня написать эту статью посредством плодотворных дискуссий.

Ссылки:

[1] Заметьте, что слово “внеземной” используется как прилагательное или описывающее слово, а не существительное. Словарь определяет это слово как “возникшее, расположенное и происходящее вне Земли”. Издатель верит, что это ссылка на разум выше Земного плана (пример – Духовный разум, Все, Что Есть, Творец и т.д.)

[2] Варолиев мост – полоса нервных волокон на поверхности желудочка ствола мозга, связывающая продолговатый мозг и мозжечок с верхними частями мозга. (Примечание переводчика)

[3] (Прим. перев.) Перикард – околосердечная сумка.

[4] Прим. перев. Выражение “перемотка контуров” заимствовано из Книги 7 Крайона “Письма из дома”. Перевод Дениса Гапеева, под редакцией А. Костенко. ИД “София”, 2005, стр.443. Кажется, это выражение больше соответствует смыслу, чем “переэлектрификация”.

[5] Прим перев.: эукариот – организм, клетки которого имеют оформленное ядро.

1 A. Detela. Sintropni pojavi v biopolju kot osnova informacijskih procesov v zivih organizmih, 2. slovenski forum kognitivnih znanosti, 1996 (Slovene reprint in this book)/

2 K.H. Pribram: Some dimensions of remembering: Steps toward a neuropsychological model of memory, in Macromolecules and Behavior, (ed. J. Gaito), Ac.Press 1966, pp. 165-187

K.H. Pribram: Languages of the brain: Experimental paradoxes and principles in neuropsychology, Prentice-Hall 1971

K.H. Pribram, M. Nuwer, R. Baron: The holographic hypothesis of memory structure in brain function and perception, zbornik Contemporary Developments in Mathematical Psychology, W.H. Freeman, San Francisco 1974

3 B.A. Brennan: Hands of Light (Bantam Books, 1085), chapter 4

4 P.M. Morse, H. Feshbach: Methods of Theoretical Physics (McGraw-Hill, 1953), p. 1301

5 K. Huang, R. Tipton: Vortex excitations in the Weinberg-Salam theory, Phys. Rev. D. 23 (1981) 3050

6 Lee Neuwirth: The theory of knots, Sci. Am. June 1979, pp. 84-96

7 F. Krizanic; Vektorji, matrike,tenzorji (Sigma, Lubljana 1962)

8 R.P. Feynman: Lectures on physics (Addison-Wesley), vol. II, chapter 27

9 D.H. Parkinson, B.E. Mulhall, The generation of high magnetic fields, Plenum press 1967, p. 154

10 F. Capra: The Web of Life (Anchor Books 1996)

11 I. Prigogine, I. Stengers: Order out of Chaos, Bantam 1984

12 M. Jibu, K. Yasue: Quantum Brain Dynamics and Consciousness (John Benjamins, Amsterdam 1995)

13 R. Penrose: Shadows of the Mind (Oxford Univ. Press 1994)

14 L.E. Ballentine: Quantum Mechanics (Prentice Hall 1990)

15 R. Turton: The Quantum Dot (Freeman Spectrum, 1995)

16 A. Detela: Dusevni procesi v zivih organismih – izziv za sodobno fiziko, 1995 (Slovene reprint in this book).

17 R.P. Feynman: The same equations have the same solutions (Lecrures on physics, vol. II/12-1)

18 J. Gleick: Chaos, Penguin books 1987

19 P. Coveney, R. Highfield: The Arrow of Time (1990)

20 Time’s Arrow Today (ed. S.F. Savitt), Cambridge University Press 1995

21 For instance, Applied Optics and Optical Engineering, Vol. 1, ch. 9 (R.J. Meltzer), p. 347

22 S.R. Hameroff, R.C. Watt: Information processing in microtubules, J.theor.Biol. 98 (1982) pp. 549-561

23 R.D. Allen: The microtubule as an intracellular engine, Sci. Am., Febr. 1987

ПРИЛОЖЕНИЕ: ДРУГИЕ ПРИМЕРЫ СИНТРОПИЧЕСКОГО ПОВЕДЕНИЯ

Количественный анализ показывает, что синтропические условия, возможно, больше всего выполняются в следующих природных структурах:

• биополе

• биомолекулах со сложными электронными состояниями (ДНК, микротрубочки...)

• сложных сверхпроводящих паутинообразных структурах

• возможно, шаровой молнии

• внутри элементарных частиц.

Дальнейшее изучение этих явлений “умоляет” о новом знании об очень интересных формах материи, где события могут описываться совершенно другими и все еще неизвестными законами.

Намеченная выше теория биополя – возможный шаблон для других синтропических структур. Определенные количественные параметры другие (например, структурные периоды и частоты), но большинство вновь представленных идей сохраняют свое значение.

Сложные биомолекулы – крошечные (но крайне мощные) квантовые компьютеры, похожие на будущие наночипы, основанные на связанных квантовых состояниях в трехмерных сетях (узловых структурах) крошечных сверхпроводящих путей и тоннелирующих переключателей.

Шаровая молния обладает очень сильным магнитным полем (> 10Т), ее заметная устойчивость может быть легко объяснена той же самой моделью, то есть магнитными линиями и направлениями течения электрического потока, сплетенными вместе в самоорганизующуюся ткань.

Любопытно, что элементарные частицы удовлетворяют тем же самым синтропическим условиям. Квантовые частицы – устойчивые синтропические структуры, возможно. похожие на шаровую молнию. Свойства симметрии синтропических структур приводят к хорошо известной CПT инвариантности. Хотя вихревая модель электрона или фотона не нова, эта картина сейчас обретает хороший математический фундамент, базирующийся на самоорганизующемся эфире (квантовом вакууме). Здесь возникает много философских вопросов: если, по определению, не обладающий первичной структурой и отличительными качествами эфир является нашим проявленным миром (пространством-временем), то очевидный результат всеобъемлющей синтропической активности (в Ведической философии, воспринимаемый мир) является майей (иллюзией), взаимодействием Шивы и Шакти?

Не легко ответить на вопросы о более глубокой природе квантовых состояний. Перед нами - обширное и неисследованное поле. Можно воспользоваться новыми математическими инструментами (такими, как нечеткая (размытая) логика и сложные топологии пространственно-временных структур) и попытаться понаблюдать за синтропической активностью в эфире. Можно найти новые глубокие определения информационной взаимосвязи в квантовых состояниях. Будут ли он

Date: 2015-07-27; view: 485; Нарушение авторских прав