
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Построение графиков в электронной таблице Excel
|
|
Построить в электронной таблице Excel графики параметрически заданной функции при разных значениях
конcтант а, b, l. Оси графика – х и y, которые зависят от аргумента t или j
| № | Название кривой | Вид графика | Параметрические уравнения | Диапазон аргумента | Кол-во граф. | Значения констант |
| Циклоида | 
| x = a×(t - sin t) y = a×(1 - cos t) | t Î 0 ¸ 6×p Шаг 0,5 | a = 1; 1.25; 1.5; 1.75; 2 | ||
| Циклоида | 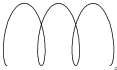
| x = a×(t - l× sin t) y = a×(1 - l× cos t) | t Î 0 ¸ 6×p Шаг 0,5 | a = 2 l = 0.4; 0.7; 1.0; 1.3; 1.6; 2.0 | ||
| Трохоида | 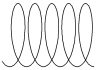
| x = a×t - b× sin t y = a - b× cos t | t Î 0 ¸ 10×p Шаг 0,1 | a = -1 b = 0.1; 1; 2; 3; 4 | ||
| Эпитрохоида | 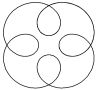
| x = a× cos (l×t) - b× cos (t + l×t) y = a× sin (l×t) - b× sin (t + l×t) | t Î 0 ¸ 10×p Шаг 0,5 | a = 0; 1; 2; 3; 10; 15 b = 2 l = 0.25 | ||
| Гипотрохоида | 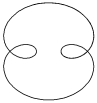
| x = a× cos (l×t) - b× cos (t - l×t) y = a× sin (l×t) - b× sin (t - l×t) | t Î 0 ¸ 10×p Шаг 0,5 | a = 0; 1; 2; 3; 10; 15 b = 2 l = 0.25 | ||
| Декартов лист | 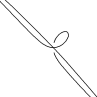
| x = a×t / (1 + t3) y = a× t2 / (1 + t3) | t Î -6 ¸ 6 t ¹ -1 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | ||
| Циссоида Диоклеса | 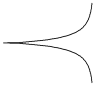
| x = a× t2 / (1 + t2) y = a× t3 / (1 + t2) | t Î -6 ¸ 6 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | ||
| Строфоида | 
| x = a× (t2 - 1) / (t2 + 1) y = a×t×(t2 - 1) / (t2 + 1) | t Î -6 ¸ 6 Шаг 0,2 | a = 1; 2; 3; 4; 5; 6 | ||
| Конхоида Никомеда | 
| x = a + b× cos t y = a× tg t + b× sin t | t Î 0 ¸ 10 t ¹ p/2 Шаг 0,01 | a = 2 b = 1; 10; 30; 50; 90 | ||
| Улитка Паскаля | 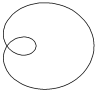
| x = a× cos 2 t + b× cos t y = a× cos t × sin t + b× sin t | t Î 0 ¸ 2×p Шаг 0,1 | a = 1; 2; 3; 4; 5; 6 b = 3 | ||
| Эпициклоида | 
| x = (a + b)×cos j - a×cos[(a + b)×j/a] y = (a + b)× sin j - a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1 b = 1; 2; 3; 4; 5; 6 | ||
| Эпициклоида | 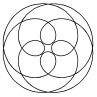
| x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 10×p Шаг 0,2 | a = 3; b = 4 l = 0.5; 0.7; 1; 1.5; 2; 3 | ||
| Эпициклоида | 
| x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1; b = 4 l = 0.5; 1; 1.5; 2; 4; 6 | ||
| Эпициклоида | 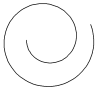
| x = (a + b)×cos j - l×a×cos[(a + b)×j/a] y = (a + b)× sin j - l×a ×sin[(a + b)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 7; b = 4 l = 0.5; 1; 2; 4; 6; 8 | ||
| Гипоциклоида | 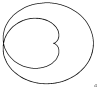
| x = (b - a)×cos j - a×cos[(b - a)×j/a] y = (b - a)× sin j - a ×sin[(b - a)×j/a] | j Î -2×p ¸ 2×p Шаг 0,1 | a = 1 b = 1.5; 2.5; 3; 3.5; 4; 5 | ||
| Гипоциклоида | 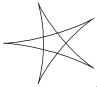
| x = (b - a)×cos j - a×cos[(b - a)×j/a] y = (b - a)× sin j - a ×sin[(b - a)×j/a] | j Î 0 ¸ 6×p Шаг 0,5 | a = 1.5; 2; 2.5; 3; 3,5; 4 b = 1 | ||
| Гипоциклоида | 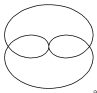
| x = (b - a)×cos j - l×a×cos[(b - a)×j/a] y = (b - a)× sin j - l×a ×sin[(b - a)×j/a] | j Î 0 ¸ 2×p Шаг 0,1 | a = 1; b = 4 l = 0.5; 1; 1.5; 2; 3; 4 | ||
| Гипоциклоида | 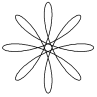
| x = (b - a)×cos j - l×a×cos[(b - a)×j/a] y = (b - a)× sin j - l×a ×sin[(b - a)×j/a] | j Î 0 ¸ 10×p Шаг 0,2 | a = 5; b = 2 l = 0.2; 0.5; 0.7; 1; 1.5; 2 | ||
| Спираль | 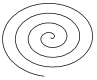
| x = a×t× cos t y = b×t× sin t | t Î 0 ¸ 10×p Шаг 0,5 | a = 2 b = -2; -1; 1; 2; 3; 4 | ||
| Гиперболич. спираль | 
| x = (a× cos t) / t y = (b × sin t) / t | t Î -6 ¸ 6 t ¹ 0 Шаг 0,1 | a = 2 b = 1; 2; 3; 4; 5 | ||
| Гиперболич. спираль | 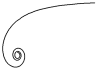
| x = (a× cos t) / t y = (b × sin t) / t | t Î 0.5 ¸ 20 Шаг 0,5 | a = 3 b = 1; 2; 3; 4; 5 | ||
| Астроида | 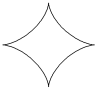
| x = a× cos 3 (t / 4) y = b × sin 3 (t / 4) | t Î 0 ¸ 8×p Шаг 0,1 | a = 2 b = 1; 2; 3; 4; 5 | ||
| Астроида | 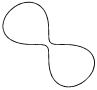
| x = a× cos 3 (t – b) y = a × sin 3 t | t Î 0 ¸ 8×p Шаг 0,2 | a = 2 b = 0; 1; 2; 3; 4 | ||
| Астроида | 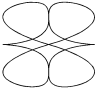
| x = a× cos 3 (b×t) y = a × sin 3 t | t Î 0 ¸ 8×p Шаг 0,1 | a = 2 b = 0.5; 1; 1.5; 3; 3.5 | ||
| Эвольвента | 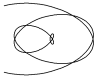
| x = a× cos t + a×t × sin t y = a × sin t + a×t× cos t | t Î -10 ¸10 Шаг 0,5 | a = -2; -1; 1; 2 | ||
| Эвольвента | 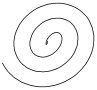
| x = a× cos t + a×t × sin t y = a × sin t + a×t× cos t | t Î 0 ¸20 Шаг 0,5 | a = -2; -1; 1; 2 | ||
| Эллипс | 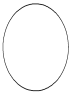
| x = a× cos t y = b × sin t | t Î 0 ¸ 2×p Шаг 0,5 | a = 7 b = 1; 4; 7; 10; 13 | ||
| Эллипс | 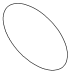
| x = a× cos (c + t) y = b × sin (c - t) | t Î 0 ¸ 2×p Шаг 0,11 | a = 3 b = 2 b = 1; 2; 3; 4; 5 |
| <== предыдущая | | | следующая ==> |
| Основные характеристики источников искусственного света | | | Глава 1 |
Date: 2015-07-27; view: 3086; Нарушение авторских прав