
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интегрируя зависимости (1.7) и (1.8), получим
|
|
Qy = Qo - qy × z и 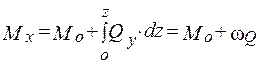 , (1.9)
, (1.9)
где Qo и Mо соответственно поперечная сила и изгибающий момент в начале участка, w Q – площадь эпюры Q от начала участка до рассматриваемого сечения.
В частности, если qy = ± q = const, то формулы (1.9) принимают
вид 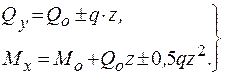 (1.10)
(1.10)
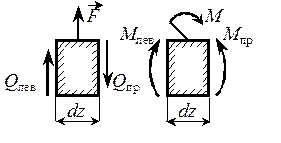 Рис. 1.12 Рис. 1.12
| Рассматривая равновесие элемента, выделенного на границе двух смежных участков и нагруженного сосредоточенной силой F (рис. 1.12) |
или сосредоточенным моментом М, находим
 (1.11)
(1.11)
Знак “минус” соответствует нагрузке, противоположной указанной на рис. 1.12.
При построении эпюры Qy положительные значения поперечной силы принято откладывать вверх, а отрицательные вниз. Н а э п ю р е Мх ординаты откладываются со стороны растянутых волокон, что с учетом правила знаков для изгибающих моментов означает: п л ю с - в н и з, м и н у с - в в е р х.
На основании формул (1.10) и (1.11) можно сформулировать следующие п р а в и л а п о с т р о е н и я э п ю р Qy и Мх:
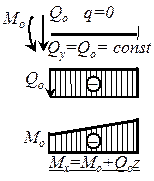
| 1. На участке, свободном от погонной нагрузки (q = 0), поперечная сила постоянна, а изгибающий момент изменяется по линейному закону. |
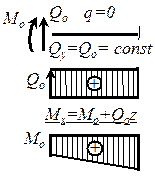
|
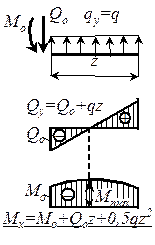
| 2. На участке с равномерно распределенной нагрузкой поперечная сила изменяется по линейному закону, а изгибающий момент описывается уравнением квадратной параболы, обращенной выпуклостью в сторону нагрузки. В сечении, где Qy = 0, Мх имеет экстремум. |

|
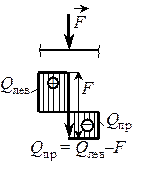
| 3. Под сосредоточенной силой 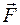 на эпюре Qy происходит скачок на величину этой силы (при обходе слева направо скачок совпадает с направлением силы!). на эпюре Qy происходит скачок на величину этой силы (при обходе слева направо скачок совпадает с направлением силы!).
| 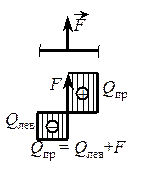
|
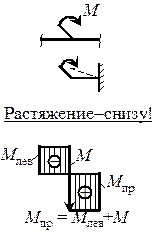
| 4. В сечении, где к балке приложен сосредоточенный момент М, на эпюре Мх возникает скачок, равный по величине приложенному моменту. Направление скачка зависит от направления момента: если момент вызывает растяжение нижних волокон, то скачок происходит вниз и наоборот. |
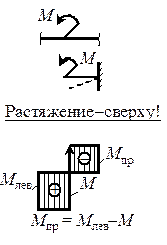
|
| Р а м о й называется система, состоящая из стержней, жестко соединенных в узлах. В поперечных сечениях рамы возникает три внутренних силовых фактора: продольная Nz и поперечная Qy силы, а также изгибающий момент Мх. Для поперечной силы сохра- |
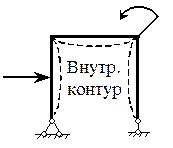
|
няется правило знаков, принятое в балках. Изгибающий момент считается положительным, если он вызывает растяжение волокон, расположенных со стороны внутреннего контура.
П р и м е р 1.7
Построить эпюры Qy и Мх для балки с консолью.
Р е ш е н и е
1. Определение опорных реакций. Составляем уравнения равновесия:
å mB = 0,
RA ×2 a - qa2 - qa × a /2 = 0,
откуда  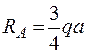 , ,
|  Рис. 1.13
Рис. 1.13
|
å mА = 0, RВ ×2 a - qa2 - qa ×5 a /2 = 0, откуда RB = (7/4) qa.
Проверка: å y = 0, RA - RB + qa = 3 qa /4 - 7 qa /4 + qa º 0.
2. Построение эпюр поперечной силы и изгибающего момента.
Э п ю р а Qy. В сечении А происходит скачок вниз на величину реакции RA и QA = - RA. На всем протяжении участков АС и СВ распределенная нагрузка отсутствует (q = 0), поэтому эпюра Qy представляется отрезком прямой, параллельной оси абсцисс. Наличие пары сил на эпюре Qy не отражается. В сечении В происходит скачок вверх, равный по величине приложенной реакции RB, и правее этого сечения имеем QBD = QBC + RB = -3 qa /4 + 7 qa /4 = qa. На участке BD поперечная сила изменяется по линейному закону (Qy = Qo - qz) от Qo = QBD = qa до QD = QBD - qa = 0. По условию загружения балки в сечении D нет сосредоточенной силы, поэтому QD = 0. Совпадение значений QD, полученных независимо друг от друга, служит проверкой правильности построения эпюры Qy.
Э п ю р а Мх. Она строится по формуле Мх = Мо + w Q. На опоре А нет пары сил, поэтому МА = 0. На участке АС момент изменяется по линейному закону. Находим момент в сечении, бесконечно близком слева от точки С: МСА = Мо + w abcd = -(3/4) qa × a = -3 qa 2/4. По двум точкам (А и С) строим наклонную прямую. Пара сил, приложенная в сечении С, вызывает растяжение нижних волокон балки при движении слева направо, поэтому на эпюре Мх скачок вниз и в бесконечно близком сечении справа от точки С изгибающий момент равен: MCB = MCA + qa 2 = qa 2/4. Находим момент в сечении В:
MB = MCB + w dcef = qa 2/4 - 3 qa 2/4 = - qa 2/2 и по двум точкам строим наклонную прямую. На участке BD момент изменяется по квадратичному закону, достигая в сечении D значения, равного MD = MB + w fkl = - qa 2/2 + (1/2) qa × a = 0. С другой стороны, по условию загружения балки на свободном конце MD = 0. Совпадение результатов служит проверкой правильности построения эпюры Мх. По двум точкам (В и D) приближенно строим параболу, обращенную выпуклостью вниз (в направлении нагрузки q). Вершина параболы совпадает с точкой D, так как QD = 0.
| П р и м е р 1.8 Построить эпюры Qy и Мх для простой консоли, изображенной на рис. 1.14. Р е ш е н и е 1. Определение опорных реакций. Составляем уравнения равновесия: å mA = 0, MA + F × a + M - q ×2 a ×4 a = 0, | 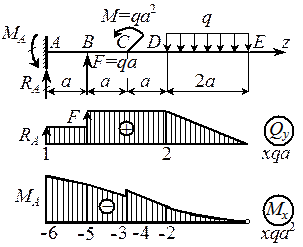 Рис. 1.14
Рис. 1.14
|
откуда MA = 6 qa 2; å Yi = 0, RA = q ×2 a - F = qa.
2. Построение эпюр поперечной силы и изгибающего момента.
Э п ю р а Qy. В сечении А имеем QA = RA (скачок на величину и в направлении реакции RA = qa). На участке АВ погонной нагрузки нет, поэтому поперечная сила постоянна. В сечении В поперечная сила меняется скачком от QBA = QA = qa до QBC = QBA + F = 2 qa (скачок на величину и в направлении силы F = qa). На участках ВС и CD поперечная сила опять сохраняет постоянное значение, т.е. QBC = QCD = 2 qa. На участке DE поперечная сила изменяется по линейному закону от QD = 2 qa до QE = QD - q ×2 a = 0.
Э п ю р а Мх. В сечении А приложен момент МА, вызывающий растяжение верхних волокон, поэтому на эпюре изгибающего момента происходит скачок вверх на величину момента MA = 6 qa 2. На участке АВ Мх изменяется по линейному закону. Вычисляем момент в сечении В
MB = MA + w Q = -6 qa 2 + qa × a = -5 qa 2 и проводим наклонную
прямую. Аналогично на участках ВС и СD. В бесконечно близком сечении слева от точки С момент равен MСB = MB + w Q = -5 qa 2 + 2 qa × a = -3 qa 2. В сечении С на эпюре Мх скачок вверх, равный приложенной паре сил M = qa 2, и правее этого сечения имеем
MCD = MCB - qa 2 = -3 qa 2 - qa 2 = -4 qa 2. Момент в сечении D MD = MCD + w Q = -4 qa 2 + 2 qa × a = -2 qa 2. На участке DE изгибающий момент изменяется по закону квадратной параболы, обращенной выпуклостью вниз (в сторону погонной нагрузки q). В сечении Е по условию загружения балки МЕ = 0. По двум точкам D и Е приближенно строим параболу.
 Рис. 1.15
Рис. 1.15
| П р и м е р 1.9 Построить эпюры Qy и Мх для балки (рис. 1.15). Р е ш е н и е. 1. Определение опорных реакций. Составляем уравнения равновесия: å mB = 0, q ×4 a × a + qa 2 + 3 qa 2- RD ×4 a = 0, откуда RD = 2 qa; å mD = 0, RB ×4 a + qa 2 +3 qa 2- q ×4 a ×3 a = 0, откуда RB = 2 qa. |
П р о в е р к а
å Yi = 0, q ×4 a - RB - RD = 4 qa - 2 qa - 2 qa = 0.
Date: 2015-07-27; view: 403; Нарушение авторских прав