Вынужденные колебания. Резонанс.Автоколебания

Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармоническими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ₀, происходит рез­кое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ₀ внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ представлен на рисунке, этот график называется резонансной кривой:

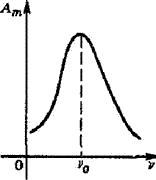
Явление резонанса играет большую роль в ря­де природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.

АВТОКОЛЕБАНИЯ - незатухающие колебания в дис-сипативной нелинейной системе, поддерживаемые за счёт энергии внеш. источника, параметры к-рых (амплитуда, частота, спектр колебаний) определяются свойствами самой системы и не зависят от конечного изменения нач. условий. Термин "А." введён А. А. Андроновым в 1928.

А. принципиально отличаются от др. колебат. процессов в диссипативных системах тем, что для их поддержания не требуется колебат. воздействий извне. Примеры А.: колебания скрипичной струны при движении смычка, тока в радиотехн. генераторе, воздуха в органной трубе, маятника в часах. Возникают А. в результате развития колебат. неустойчивостей с их последующей стабилизацией из-за прекращения поступления энергии от источника или прогрессирующего возрастания потерь (диссипации). Режим стационарных А. определяется из условия энергетич. баланса - в ср. за период диссипативные траты энергии Q (I) (I - интенсивность А.) должны точно компенсироваться поступлением энергии W(I)от источника:

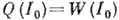
Автоколебания, незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются свойствами самой системы. Этим Автоколебания отличаются от вынужденных колебаний, амплитуда и период которых определяются характером внешнего воздействия (приставка «авто» и указывает на то, что колебания возникают в самой системе, а не навязываются внешним воздействием). Автоколебания отличаются и от свободных колебаний (например, колебаний свободно подвешенного маятника, колебаний силы тока в электрическом контуре) тем, что, во-первых, свободные колебания постепенно затухают, во-вторых, их амплитуда зависит от первоначального «толчка», создающего эти колебания. Примерами Автоколебания могут служить колебания, совершаемые маятником часов, колебания струны в смычковых или столба воздуха в духовых музыкальных инструментах, электрические колебания в ламповом генераторе (см. Генерирование электрических колебаний). Системы, в которых возникают Автоколебания, называются автоколебательными.

Автоколебательные системы во многих случаях можно разделить на 3 основных элемента: 1) колебательную систему (в узком смысле); 2) источник энергии, за счет которого поддерживаются Автоколебания, и 3) устройство, регулирующее поступление энергии из источника в колебательную систему. Эти 3 основных элемента могут быть отчётливо выделены, например, в часах, в которых маятник или баланс служит колебательной системой, пружинный или гиревой завод — источником энергии, и, наконец, анкерный ход — механизмом, регулирующим поступление энергии из источника в систему. В ламповом генераторе колебательной системой служит контур, содержащий ёмкость и индуктивность и обладающий малым активным сопротивлением; выпрямитель (или батарея), питающий напряжением анод лампы, является источником энергии, а электронная лампа с элементом обратной связи — устройством, регулирующим поступление энергии из источника в колебательный контур.

В часах, например, Автоколебания осуществляются следующим образом (рис.). При прохождении качающегося балансира 1 через определённое положение (обычно дважды за период) спусковое устройство 2 и 3 подталкивает колесо балансира, сообщая ему энергию, необходимую для того, чтобы компенсировать потерю энергии за полпериода колебаний. Балансир часов совершает Автоколебания с амплитудой, целиком определяемой свойствами часового механизма. Однако для того, чтобы эти Автоколебания возникли, обычно нужно не только завести пружинный завод, но и слегка встряхнуть часы, т. е. сообщить начальный толчок балансиру. Т. о., часы — это в большинстве случаев автоколебательная система без самовозбуждения. В духовых инструментах продувание струи воздуха поддерживает Автоколебания столба воздуха в трубе инструмента, а в струнных смычковых инструментах Автоколебания поддерживаются силой трения, действующей между смычком и струной.

Чтобы колебания были незатухающими, поступающая из источника в систему энергия должна компенсировать потери энергии в самой системе. Такая компенсация происходит в целом за период колебаний; но в одни части периода поступающая энергия может превышать потери в системе, в другие, наоборот, потери в системе могут превышать поступление энергии в неё. То значение амплитуды колебаний, при котором происходит компенсация потерь в целом за период, и является стационарным (не изменяющимся со временем) значением амплитуды Автоколебания Такой баланс поступления и потерь энергии оказывается возможным только при определённых значениях амплитуды Автоколебания (в простейших случаях только при одном значении).

Обычно при значениях амплитуды колебаний, меньших стационарной, поступление энергии в систему превышает потери в ней, вследствие чего амплитуда колебаний возрастает и достигает стационарного значения. В частности, если в систему поступает энергия больше, чем теряется в ней при сколь угодно малых амплитудах колебаний, то происходит самовозбуждение колебаний. Наоборот, при амплитудах, превышающих стационарное значение, потери энергии в системе обычно превышают поступление энергии из источника, вследствие чего амплитуда колебаний уменьшается и также достигает стационарного значения. Т. о., отклонения амплитуды Автоколебания в ту или другую сторону от стационарного значения затухают, и Автоколебания в этих случаях устойчивы.

Однако в некоторых случаях отклонение амплитуды колебаний от стационарного значения и нарушение компенсации потерь энергии в системе приводят к дальнейшему росту отклонений амплитуды от стационарного значения. Это будет иметь место, если при уменьшении амплитуды потери начинают преобладать над поступлением энергии или, наоборот, при увеличении амплитуды поступление энергии начинает преобладать над потерями. В этом случае Автоколебания неустойчивы, и, вследствие наличия во всякой реальной системе неизбежных возмущений и толчков, такие Автоколебания длительное время существовать не могут.

Форма Автоколебания может быть различной. Если добротность колебательной системы велика, т. е. потери энергии в колебательной системе относительно малы, то для поддержания Автоколебания в систему за период должно поступать количество энергии, очень малое по сравнению с полной энергией колебательной системы. При этом характер происходящих процессов почти не изменяется по сравнению с тем, как они протекали бы в системе без поступления энергии. В этом случае период и форма Автоколебания будут очень близки к периоду и форме собственных колебаний колебательной системы; если собственные колебания в системе по форме близки к гармоническим, то Автоколебания также близки к гармоническим.

В систему с малой добротностью для поддержания Автоколебания должна поступать энергия, уже не малая по сравнению с энергией системы, что может существенно изменить характер происходящих в ней процессов; в частности, форма Автоколебания может значительно отличаться от синусоидальной. Если за период Автоколебания рассеивается вся накопленная в системе энергия (т. е. система уже не колебательная, а апериодическая), то Автоколебания могут очень сильно отличаться по форме от синусоидальных, т. е. превратиться в т. н. релаксационные колебания.

Возможность установления баланса энергии только при определённых значениях амплитуды Автоколебания обусловлена наличием в системе т. н. нелинейного элемента, свойства которого зависят от состояния системы (например, сопротивления, которое зависит от приложенного к этому сопротивлению напряжения).
4.Затухающие коллебания. логарифмический фискремент затухания.

Рассмотрим процесс превращения энергии при гармоническом колебательном движении на примере идеального (F_тр=0)

5.Уравнение волны.Поток энергии волны. Уравнение Уманова.

.Волна, как известно, это процесс распространения колебаний в пространстве. Чтобы волна в среде могла распространяться, точки среды должны быть связаны между собой силами, способными вызвать колебания, то есть силами упругости. На рисунке 1 показан ряд таких связанных между собой точек. Если одна из точек, например точка O, начинает колебаться, то ее колебания передаются в направлении r.

/index.php/%D0%A4%D0%B0%D0%B9%D0%BB:Img_Kvant-1984-11-004.jpg

Пусть точка O колеблется вдоль оси X по закону

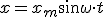
. (1)

Здесь время t отсчитывается от момента, когда точка О находилась в положении равновесия. Ее колебания передаются другим точкам не мгновенно, а с некоторой скоростью υ. Это значит, что за единицу времени колебание доходит до точки в ряду, расположенной от точки О на расстоянии, численно равном υ. Расстояние же, на которое колебание распространяется за время, равное одному периоду T колебаний, называется длиной волны λ («Физика 10», с. 81). Отсюда следует, что

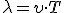
или, так как

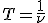
, то

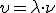
. (1)

Любая точка в нашем ряду (см. рис. 1), как только до нее дойдет волна, начнет колебаться с той же частотой, что и точка О, то есть будет повторять эти колебания. Но повторять с некоторым запозданием — ведь до точки, находящейся от О на расстоянии r, колебание дойдет через промежуток времени, равный

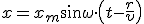
. Поэтому для координаты х точки на расстоянии r мы должны написать

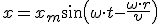
. (2)

Уравнение (2) называется уравнением волны. Оно позволяет найти смещение х от положения равновесия любой точки (находящейся на любом расстоянии r) в любой момент времени. Для данного момента времени оно дает как бы фотографию положений всех точек ряда относительно оси X. Уравнение волны показывает, что все точки действительно совершают одинаковые колебания (все колеблются вдоль оси X, и у всех одинаковые амплитуда и частота колебаний). Неодинаковы только фазы колебаний — разность фаз колебаний двух точек, расстояние между которыми равно Δ r, составляет

.

Иногда уравнение волны удобнее представить несколько иначе. Перепишем уравнение (2) в виде

.

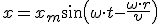
Подставим во второй член в скобках вместо скорости волны υ равную ей величину λν, а вместо ω напишем 2 πν. Тогда получим

. (3)

Из этого выражения видно, что координата х любой точки на расстоянии r от источника волны зависит от величины, то есть от числа длин волн, укладывающихся на расстоянии r. Если, например, r = λ, то отставание по фазе будет равно 2 π, а это значит, что фаза колебаний этой точки будет такая же, как и точки О. Точно так же, если r = 2 λ, 3 λ и т. д., то сдвиг фазы будет равен 4 π, 6 π и т. д., то есть и в этом случае фазы будут одинаковыми. Таким образом, точки волны, находящиеся друг от друга на расстоянии, равном длине волны, двум длинам волн, вообще целому числу длин волн, колеблются в одинаковых фазах.

Уравнение волны (3) позволяет легко получить условия максимумов и минимумов при интерференции волн (о которых говорится в «Физике 10» на с. 94). Напомним, что вопрос об интерференции возникает тогда, когда в некоторую точку пространства приходят две волны, каждая из которых приносит в эту точку колебания. Поэтому точка, где «встретились» две волны, участвует в двух колебаниях. Результат же сложения двух колебаний зависит от разности фаз складывающихся колебаний.

Допустим, что в некоторую точку С пришли две волны, источники которых — точки А и В — отстоят от С на расстояния r ₁ и r ₂ (рис. 2). Тогда в точке С складываются два колебания, происходящие вдоль одной оси:

.

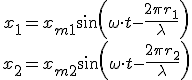
/index.php/%D0%A4%D0%B0%D0%B9%D0%BB:Img_Kvant-1984-11-005.jpg

Разность фаз этих колебаний равна 2л

.

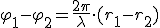
Поэтому условие усиления (максимумов) имеет вид

,

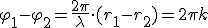
где k = 0, 1, 2,..., откуда

— колебания будут усилены (то есть амплитуда сложного.колебания будет равна сумме амплитуд складываемых колебаний), если разность хода r ₁ — r ₂ волн до места «встречи» равна четному числу полуволн. Соответственно условие минимумов —

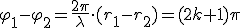
— колебания будут ослаблены (результирующая амплитуда будет равна разности амплитуд колебаний в двух волнах), если разность хода волн равна нечетному числу полуволн.

Умова вектор, вектор плотности потока энергии физического поля; численно равен энергии, переносимой в единицу времени через единичную площадку, перпендикулярную направлению потока энергии в данной точке. Назван по имени Н. А. Умова, впервые (1874) введшего общее понятие о потоке энергии в сплошной среде (на основе закона сохранения энергии). Плотность потока энергии электромагнитного поля была определена на основе Максвелла уравнений англ. физиком Дж. Пойнтингом и называется Пойнтинга вектором.

Date: 2015-08-15; view: 1870; Нарушение авторских прав