
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание состоит из 11 задач
|
|
Номер варианта задания определяется последней цифрой зачетной книжки студента.
Задача 1 (ЭММ и М, тема 2)
Дана номинальная годовая процентная ставка 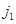 с соответствующим числом
с соответствующим числом 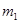 капитализаций процента в году. Требуется найти:
капитализаций процента в году. Требуется найти:
1) коэффициент наращения б, коэффициент дисконтирования д и эффективную процентную ставку для периода времени, равного t лет;
2) эквивалентную заданной номинальную годовую процентную ставку  с числом
с числом  капитализаций процента в году.
капитализаций процента в году.
| Номер варианта | ||||||||||
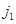
| 14% | 16% | 15% | 18% | 17% | 19% | 21% | 20% | 22% | 10% |
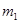
| ||||||||||
| t | 1/6 | 1/4 | 1/2 | 1/3 | 2/3 | 3/4 | 1/2 | 5/6 | 1/3 | 1/2 |

|
Задача 2 (ЭММ и М, тема 3)
Последовательность платежей состоит из трех платежей размером  ,
, 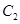 и
и 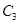 денежных единиц, срок выплаты которых, соответственно,
денежных единиц, срок выплаты которых, соответственно, 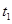 ,
, 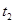 и
и 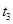 лет. Эффективная годовая процентная ставка равна r.
лет. Эффективная годовая процентная ставка равна r.
Требуется найти:
1) текущие стоимости отдельно взятых платежей и последовательности платежей;
2) продолжительность последовательности платежей и с ее помощью оценить относительное изменение текущей стоимости последовательности платежей при изменении процентной ставки, равном 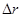 .
.
| Номер варианта | ||||||||||

| ||||||||||
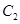
| ||||||||||
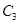
| ||||||||||
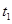
| 1,5 | 0,5 | 2,5 | 1,5 | 2,5 | 0,5 | ||||
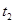
| 2,5 | |||||||||
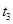
| 3,5 | 1,5 | 3,5 | 2,5 | ||||||
| r | 16% | 15% | 18% | 10% | 8% | 6% | 12% | 14% | 11% | 17% |
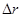
| -1% | 1,2% | -1,5% | 1,5% | -0,8% | 0,7% | -0,6% | 0,4% | -0,5% | 0,8% |
Задача 3 (ЭММ и М, тема 3)
Пусть размер рентного платежа равен R денежных единиц, срок ренты – t лет, число рентных платежей в году – 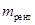 , номинальная годовая процентная ставка – j, число капитализаций процента в году – m. Требуется:
, номинальная годовая процентная ставка – j, число капитализаций процента в году – m. Требуется:
1) найти текущую и будущую стоимости ренты;
2) найти продолжительность ренты и с ее помощью оценить относительное изменение текущей стоимости ренты при изменении номинальной годовой процентной ставки, равном D j.
| Номер варианта | ||||||||||
| R | ||||||||||
| t | ||||||||||
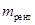
| ||||||||||
| j | 14% | 16% | 12% | 18% | 15% | 10% | 20% | 17% | 19% | 11% |
| m | ||||||||||
| D j | 0,8% | -1,4% | 1,6% | -1,5% | 0,9% | -0,8% | 0,7% | -0,5% | 0,6% | -1,2% |
Задача 4 (ЭММ и М, тема 4)
Начальные инвестиции в проект равны  , коэффициент прибыли –
, коэффициент прибыли – 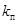 для всех лет, коэффициент реинвестирования –
для всех лет, коэффициент реинвестирования – 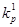 для первого года,
для первого года,  для второго года, и
для второго года, и 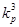 для всех последующих лет (начиная с третьего). Внутренняя доходность альтернативных проектов – r. Требуется:
для всех последующих лет (начиная с третьего). Внутренняя доходность альтернативных проектов – r. Требуется:
1) определить свободные денежные потоки для первого, второго и третьего лет;
2) оценить рыночную стоимость проекта в начале третьего года;
3) определить текущую и чистую текущую стоимости проекта;
4) записать уравнение для определения внутренней доходности проекта и решить это уравнение на ЭВМ средствами Excel.
| Номер варианта | ||||||||||

| ||||||||||
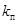
| 40% | 25% | 30% | 35% | 45% | 42% | 32% | 28% | 34% | 36% |
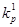
| 91% | 83% | 70% | 87% | 82% | 95% | 92% | 74% | 65% | 62% |

| 72% | 64% | 65% | 67% | 53% | 45% | 38% | 63% | 52% | 48% |
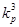
| 24% | 30% | 28% | 22% | 15% | 12% | 14% | 18% | 19% | 17% |
| r | 26% | 19% | 24% | 25% | 22% | 23% | 27% | 18% | 28% | 23% |
Задача 5 (ЭММ и М, тема 5)
Номинальная стоимость облигации равна F денежных единиц, номинальная годовая купонная ставка – jкуп, число купонных платежей в году – mкуп, срок погашения облигации – t лет, цена облигации – P денежных единиц, эффективная годовая доходность альтернативных облигаций –  . Требуется:
. Требуется:
1) записать уравнение для определения эффективной доходности облигации для купонного периода и решить это уравнение на ЭВМ средствами Excel;
2) найти текущую стоимость облигации;
3) найти продолжительность облигации и с ее помощью оценить относительное изменение текущей стоимости облигации при изменении эффективной годовой доходности альтернативных облигаций на 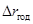 процентов.
процентов.
| Номер варианта | ||||||||||
| F | ||||||||||
| jкуп | 14% | 16% | 12% | 18% | 15% | 10% | 20% | 14% | 19% | 11% |
| mкуп | ||||||||||
| t | ||||||||||
| P | ||||||||||

| 12% | 14% | 11% | 16% | 13% | 15% | 18% | 17% | 20% | 21% |
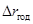
| 0,8% | -1,4% | 1,6% | -1,5% | 0,9% | -0,8% | 0,7% | -0,5% | 0,6% | -1,2% |
Задача 6 (ЭММ и М, тема 6)
Портфель активов финансовой организации состоит из 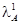 восьмилетних 20%-ных облигаций и
восьмилетних 20%-ных облигаций и 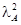 шестилетних 15%-ных облигаций. Купонный период облигаций – один год, номинальная стоимость – 100 д.е. Рыночные цены этих облигаций равны их номинальным стоимостям.
шестилетних 15%-ных облигаций. Купонный период облигаций – один год, номинальная стоимость – 100 д.е. Рыночные цены этих облигаций равны их номинальным стоимостям.
Портфель обязательств финансовой организации состоит из 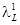 трехлетних 10%-ных облигаций с годовой эффективной доходностью
трехлетних 10%-ных облигаций с годовой эффективной доходностью 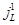 и с купонным периодом – один год, и
и с купонным периодом – один год, и  двухлетних бескупонных облигаций с годовой эффективной доходностью
двухлетних бескупонных облигаций с годовой эффективной доходностью 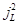 . Номинальная стоимость облигаций – 100 д.е.
. Номинальная стоимость облигаций – 100 д.е.
Требуется:
1) найти рыночные стоимости портфелей активов и обязательств, рыночную стоимость собственного капитала финансовой организации и финансовый рычаг;
2) продолжительность портфелей активов и обязательств;
3) оценить изменение рыночной стоимости собственного капитала финансовой организации при заданном значении 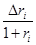 , где
, где 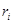 – годовые эффективные доходности облигаций.
– годовые эффективные доходности облигаций.
| Номер варианта | ||||||||||
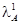
| ||||||||||
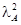
| ||||||||||
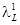
| ||||||||||

| ||||||||||
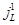
| 12% | 13% | 12% | 14% | 12% | 12% | 13% | 12% | 14% | 13% |
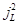
| 11% | 14% | 10% | 11% | 10% | 9% | 11% | 8% | 10% | 11% |
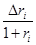
| 0,6% | -0,5% | 0,7% | 0,3% | -0,4% | -0,6% | 0,7% | 0,8% | -0,7% | 0,5% |
Задача 7 (ЭММ и М, тема 7; решить задачу на ЭВМ средствами Excel)
Известна следующая информация по кредитам:
– имел ли место дефолт для данного кредита (если да, то 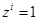 ; если нет, то
; если нет, то 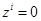 );
);
– отношение активов к оборотному капиталу заемщика (коэффициент  );
);
– отношение обязательств к собственному капиталу (коэффициент 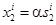 );
);
– отношение активов к прибыли (коэффициент 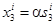 ).
).
Значения параметров 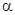 и
и  приведены ниже.
приведены ниже.
Известны также финансовые коэффициенты 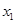 ,
, 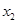 и
и  для потенциального заемщика (см. ниже).
для потенциального заемщика (см. ниже).
Требуется:
1) построить линейную регрессионную модель для оценки кредитного риска и с ее помощью оценить вероятность дефолта для потенциального заемщика (с заданными финансовыми коэффициентами 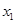 ,
, 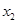 и
и  );
);
2) построить регрессионную дискриминантную модель, найти граничное значение 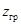 и отнести потенциального заемщика к группе с высоким либо низким кредитным риском.
и отнести потенциального заемщика к группе с высоким либо низким кредитным риском.
Номер наблюдения, 
| Информация о дефолте, 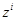
| Параметры 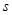
| ||

| 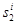
| 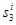
| ||
| 3,40 | 0,61 | 16,2 | ||
| 2,38 | 1,38 | 4,5 | ||
| 3,44 | 0,78 | 15,3 | ||
| 2,07 | 1,84 | 9,9 | ||
| 3,76 | 0,37 | 7,2 | ||
| 2,41 | 1,17 | 16,2 | ||
| 2,80 | 1,12 | 16,2 | ||
| 2,63 | 0,72 | 17,1 | ||
| 3,10 | 0,80 | 8,1 | ||
| 3,82 | 0,71 | 11,7 | ||
| 2,85 | 0,48 | 18,9 | ||
| 4,11 | 0,39 | 10,8 | ||
| 3,31 | 0,69 | 9,0 | ||
| 3,06 | 0,57 | 12,6 | ||
| 3,24 | 0,73 | 18,0 | ||
| 2,78 | 0,82 | 13,5 | ||
| 3,69 | 0,41 | 18,9 |
| Номер варианта | ||||||||||
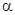
| 1,2 | 1,4 | 1,3 | 0,8 | 0,7 | 0,9 | 1,5 | 1,7 | 1,6 | 1,1 |
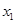
| 2,18 | 2,23 | 2,21 | 1,86 | 1,83 | 2,01 | 3,05 | 3,06 | 2,98 | 2,08 |
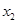
| 1,54 | 1,67 | 1,64 | 1,24 | 1,19 | 1,23 | 1,97 | 2,26 | 2,15 | 1,42 |

| 16,7 | 17,2 | 17,1 | 13,2 | 13,1 | 14,2 | 19,4 | 21,2 | 20,7 | 14,7 |
Задача 8 (ЭММ и М, тема 8; решить задачу на ЭВМ средствами Excel)
На финансовом рынке имеются акции трех компаний. Известны годовые доходности  этих акций за 12 лет. (Индекс
этих акций за 12 лет. (Индекс  соответствует виду акции, индекс
соответствует виду акции, индекс  -- номеру года).
-- номеру года).
Требуется:
1) Найти выборочные ожидаемые доходности  ,
, 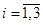 , и стандартные отклонения доходностей
, и стандартные отклонения доходностей  ,
, 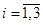 , акций заданных видов.
, акций заданных видов.
2) Построить ковариационную матрицу доходностей акций.
3) Решить задачу максимизации ожидаемой доходности портфеля при условии, что стандартное отклонение доходности портфеля не превосходит заданное значение 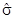 .
.
4) Решить задачу минимизации стандартного отклонения доходности портфеля при условии, что ожидаемая доходность портфеля больше либо равна заданному значению 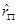 .
.
5) Решить задачу максимизации полезности  при заданном значении параметра
при заданном значении параметра 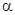 .
.
Доходности  находятся по формуле
находятся по формуле  .
.
Значения параметров 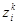 ,
,  ,
, 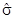 ,
, 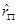 и
и 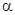 приведены ниже.
приведены ниже.

| 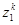
| 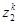
| 
|
| 11,2% | 8,0% | 10,9% | |
| 10,8% | 9,2% | 22,0% | |
| 11,6% | 6,6% | 37,9% | |
| -1,6% | 18,5% | -11,8% | |
| -4,1% | 7,4% | 12,9% | |
| 8,6% | 13,0% | -7,5% | |
| 6,8% | 22,0% | 9,3% | |
| 11,9% | 14,0% | 48,7% | |
| 12,0% | 20,5% | -1,9% | |
| 8,3% | 14,0% | 19,1% | |
| 6,0% | 19,0% | -3,4% | |
| 10,2% | 9,0% | 43,0% |
| Номер варианта | ||||||||||

| 1,3 | 0,7 | 1,4 | 0,8 | 1,2 | 1,5 | 0,9 | 1,6 | 1,1 | 1,7 |
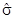
| 7,8% | 4,2% | 8,4% | 4,8% | 7,2% | 9,0% | 5,4% | 9,6% | 6,6% | 10,2% |
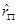
| 15,6% | 8,4% | 16,8% | 9,6% | 14,4% | 18,0% | 10,8% | 19,2% | 13,2% | 20,4% |
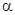
| 8,2 | 7,9 | 8,5 | 7,4 | 8,1 | 7,6 | 7,8 | 8,3 | 8,4 | 7,5 |
Задача 9 (Эконометрика, тема 3;решить задачу на ЭВМ средствами Excel)
Данные о рыночной цене коттеджей (которые строит фирма), а также об их площади, вместимости гаража и количестве комнат приведены в таблицах 1, 2 и 3.
Требуется:
1) построить линейную регрессионную модель для оценки рыночной стоимости коттеджей, и с помощью этой модели оценить рыночную стоимость коттеджа с 4 комнатами, площадью 200 кв.м., и с вместимостью гаража – 1 автомобиль;
2) с помощью t -статистик проверить гипотезы о незначимости каждого в отдельности объясняющего фактора при уровне значимости 0,1.
3) С помощью F -статистики проверить гипотезу о незначимости всех объясняющих факторов одновременно при уровне значимости 0,1.
4) Выбрать объясняющие факторы, обеспечивающие наибольшее значение скорректированного коэффициента детерминации и с помощью соответствующей модели оценить рыночную стоимость коттеджа с характеристиками, приведенными в п.1.
Таблица 1
| Номер наблюдения | Цена, ден.ед. | |||||||||
| Номер варианта | ||||||||||
Таблица 2
| Номер наблю-дения | Площадь, кв.м. | |||||||||
| Номер варианта | ||||||||||
| 111,1 | 107,8 | 112,2 | 123,2 | 118,8 | 127,6 | 124,3 | 117,7 | 113,3 | 128,7 | |
| 116,15 | 112,7 | 117,3 | 128,8 | 124,2 | 133,4 | 129,95 | 123,05 | 118,45 | 134,55 | |
| 141,4 | 137,2 | 142,8 | 156,8 | 151,2 | 162,4 | 158,2 | 149,8 | 144,2 | 163,8 | |
| 171,7 | 166,6 | 173,4 | 190,4 | 183,6 | 197,2 | 192,1 | 181,9 | 175,1 | 198,9 | |
| 181,8 | 176,4 | 183,6 | 201,6 | 194,4 | 208,8 | 203,4 | 192,6 | 185,4 | 210,6 | |
| 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 | |
| 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 | |
| 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 | |
| 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 | |
| 232,3 | 225,4 | 234,6 | 257,6 | 248,4 | 266,8 | 259,9 | 246,1 | 236,9 | 269,1 |
Таблица 3
| Номер наблюдения | Вместимость гаража | К-во комнат |
Задача 10 (Эконометрика, тема 6;решить задачу на ЭВМ средствами Excel)
Значения спроса на продукцию фирмы за каждый месяц в течение двух лет приведены в таблице. Требуется построить прогноз спроса для первых трех месяцев следующего года методом скользящего среднего (при этом необходимо определить оптимальные весовые коэффициенты и их количество).
| Месяцы | Спрос | |||||||||
| Номер варианта | ||||||||||
Задача 11 (Эконометрика, тема 6;решить задачу на ЭВМ средствами Excel)
Значения спроса на продукцию за каждый квартал в течение пяти лет приведены в таблице. Требуется построить поквартальный прогноз спроса для следующего года следующими методами:
– экспоненциального сглаживания;
– Холта (с учетом тренда);
– Винтера (с учетом тренда и сезонных колебаний).
| Квартал | Спрос | |||||||||
| Номер варианта | ||||||||||
| <== предыдущая | | | следующая ==> |
| Задача 6. Даны векторы ; ; . Если вектор такой, что = 7 и сумма косинусов углов, которые составляет с векторами | | |
Date: 2015-08-15; view: 482; Нарушение авторских прав