
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Типовой расчёт №2
|
|
студент II – ХТ – 2 Самаров А.А.
руководитель: Корнфельд С.Г.
ассистент: Стрелкова Н.Н.
Самара
2004 г.
Пусть случайные величины Х и Y принимают значение, приведённые в таблице 1.
Таблица 1
| Х | Y | X | Y | X | Y | X | Y |
1) Находим, что
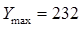
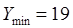
Тогда длина интервала группирования
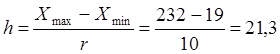
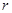 - число интервалов (разрядов), неформализован и зависит от объёма и степени однородности выборки. При
- число интервалов (разрядов), неформализован и зависит от объёма и степени однородности выборки. При 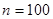 ,
, 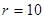
2) Находим границы величины 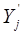
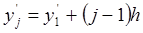 ,
, 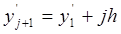
3) Находим значение представителей
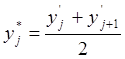
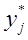 - середина j-того интервала.
- середина j-того интервала.
4) Для графического описания выборки по условиям задания необходимо построить гистограмму относительных частот (рис. 1) и эмпирическую функцию распределения 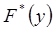 (рис. 2)
(рис. 2)
а) На гистограмме относительных частот высота прямоугольников выбирается равной 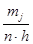 , основания прямоугольников соответствуют интервалам разбиения. Площадь j-того прямоугольника
, основания прямоугольников соответствуют интервалам разбиения. Площадь j-того прямоугольника 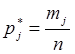 равна относительной частоте наблюдений, попавших в j-тый интервал.
равна относительной частоте наблюдений, попавших в j-тый интервал.
Составляем таблицу частот группированной выборки (табл. 2), содержащую столбцы с номерами интервала j, значениями нижней границы (начала интервала) и представителя интервала 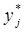 , числами значений в j-том интервале
, числами значений в j-том интервале 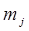 , накопленной частоты
, накопленной частоты 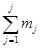 , относительной частоты
, относительной частоты 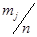 , накопленной относительной частоты
, накопленной относительной частоты 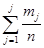 . Число строк таблицы равно числу интервалов r.
. Число строк таблицы равно числу интервалов r.
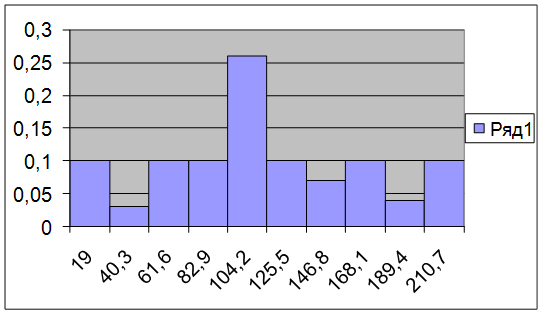
Рис. 1. Гистограмма относительных частот
б) Эмпирическая функция распределения определяется по значениям накопленных относительных частот представителей разрядов:
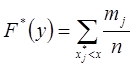
Функция представляет собой кусочно-постоянную функцию, имеющие скачки в точках, соответствующих серединам интервалов группировки 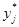 , причём при
, причём при 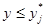
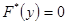 , и при
, и при 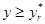
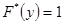
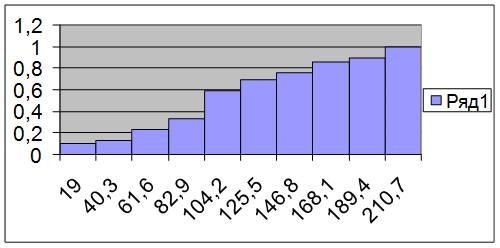
Рис. 2. Эмпирическая функция распределения 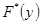
5) Составленную ранее таблицу частот группированной выборки (табл. 2) дополняем таблицей расчёта числовых значений 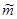 и
и 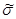 . Она содержит результаты промежуточных вычислений по формулам
. Она содержит результаты промежуточных вычислений по формулам
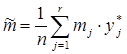
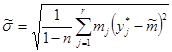
6) После заполнения таблицы 2 рассчитываем значение числовых оценок:

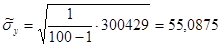
7) Определяем коэффициент вариаций
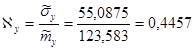
8) Определяем границы доверительного интервала для математического ожидания по формулам
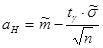
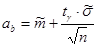
При заданной доверительной вероятности 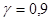 по таблицам распределения Стьюдента
по таблицам распределения Стьюдента 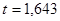 , поэтому имеем
, поэтому имеем
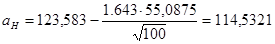
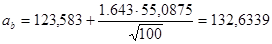
9) Среднеквадратичное отклонение оценки математического ожидания случайной величины Y равно

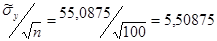
10) По виду гистограммы выдвигаем гипотезу Н0 о подчинении случайной величины нормальному закону распределения. Для построения теоретической функции 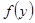 и
и 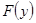 составляем таблицу значений (таблица 3) нормальной величины
составляем таблицу значений (таблица 3) нормальной величины 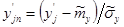 , определяем функцию Лапласа
, определяем функцию Лапласа 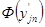 , значения функции распределения на концах отрезков
, значения функции распределения на концах отрезков 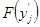 и вероятность попадания
и вероятность попадания 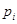 в i-тый интервал по формуле
в i-тый интервал по формуле 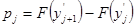
11) Рисунок 2 с эмпирической функцией распределения дополняем теоретической функцией F(y), значения которой найдены на концах интервалов.
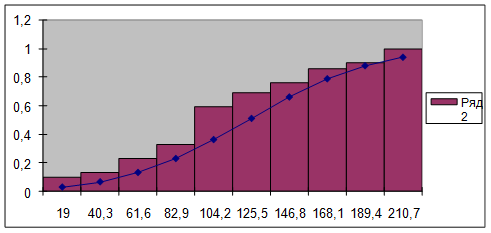
Рис. 3. Эмпирическая 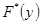 , теоретическая
, теоретическая 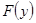 функция распределения.
функция распределения.
12) Для проверки согласия выдвинутой гипотезы о о законе распределения экспериментальным данным находим вероятность 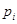 попадания опытных данных в j-тый интервал от
попадания опытных данных в j-тый интервал от 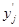 до
до 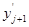 на основе полученных значений функции
на основе полученных значений функции 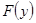 на границах интервалов. На построенную раньше гистограмму наносим точки с координатами
на границах интервалов. На построенную раньше гистограмму наносим точки с координатами 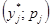 и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность
и соединяем их плавными линиями (Рис. 4). Сравнивая вид гистограммы и плотность 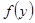 распределения, необходимо убедиться в их адекватности, близости их характеров.
распределения, необходимо убедиться в их адекватности, близости их характеров.
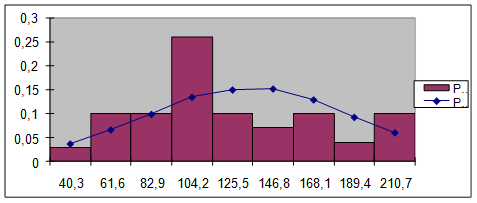
Рис. 4. Гистограмма относительных частот и теоретическая плотность вероятности 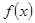 .
.
13) При количественной оценке меры близости эмпирического и теоретического законов распределения можно использовать критерии Пирсона или Колмогорова.
а) по критерию Колмогорова
Максимальное значение модуля разности между значениями эмпирической и теоретической функциями(см. рис. 2) наблюдается в точке, близкой к представителю 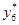 . Тогда
. Тогда
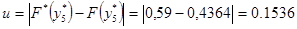
Вычисляем величину
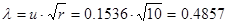
где r – объём выборки из представителей интервалов
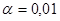 , следовательно
, следовательно 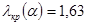 . Так как
. Так как 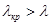 , поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
, поэтому гипотеза о нормальном распределении по критерию Колмогорова принимается как не противоречащая опытным данным.
б) Для вычисления 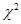 таблицу 3 дополняем промежуточными результатами
таблицу 3 дополняем промежуточными результатами 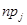 ,
, 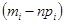 ,
, 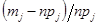 . Объединяем 1,2,3 и 9,10. Тогда
. Объединяем 1,2,3 и 9,10. Тогда 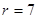 . Получаем, что
. Получаем, что
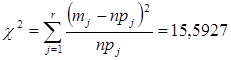
Для нормального закона распределения 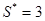 . Тогда число степеней свободы
. Тогда число степеней свободы 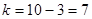 . При
. При 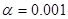 имеем
имеем 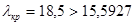 . Поэтому гипотеза по критерию
. Поэтому гипотеза по критерию 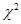 Пирсона принимается.
Пирсона принимается.
14) Составляем точечную диаграмму в декартовой системе координат, где по оси абсцисс откладываем значение 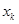 , а по оси ординат -
, а по оси ординат - 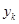 . Пары значений
. Пары значений 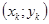 представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину
представляем на диаграмме в виде точек. На диаграмму наносим сетку равноотстоящих горизонтальных и вертикальных прямых. Расстояние между двумя вертикальными прямыми выражает длину 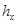 интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала
интервала по оси абсцисс, а расстояние между горизонтальными прямыми – длину интервала 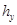 по оси ординат.
по оси ординат.
15) Для вычисления коэффициента корреляции составляется корреляционная таблица (таблица 4). В последние две строки заносятся промежуточные результаты для вычисления точечной оценки коэффициента корреляции
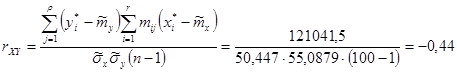
16) Находим
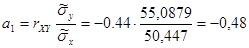
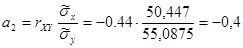

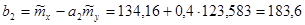
Следовательно, линейные приближения к регрессиям имеют вид:
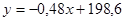
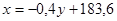
На рисунке 3 представлены точечная диаграмма и линии регрессии X на Y и Y на X. Расположение точек 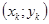 на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
на диаграмме и небольшое значение коэффициента корреляции указывают на слабую коррелированность случайных величин X и Y между собой.
Таблица 2
| № интервала | 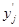
| 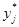
| 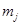
| 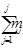
| 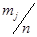
| 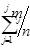
| 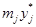
| 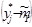
| 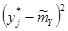
| 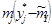
|
| 29,65 | 0,1 | 0,1 | 296,5 | -93,933 | 8823,408 | 88234,08 | ||||
| 40,3 | 50,95 | 0,03 | 0,13 | 152,85 | -72,633 | 5275,553 | 15826,66 | |||
| 61,6 | 72,25 | 0,1 | 0,23 | 722,5 | -51,333 | 2635,077 | 26350,77 | |||
| 82,9 | 93,55 | 0,1 | 0,33 | 935,5 | -30,033 | 901,9811 | 9019,811 | |||
| 104,2 | 114,85 | 0,26 | 0,59 | 2986,1 | -8,733 | 76,26529 | 1982,898 | |||
| 125,5 | 136,15 | 0,1 | 0,69 | 1361,5 | 12,567 | 157,9295 | 1579,295 | |||
| 146,8 | 157,45 | 0,07 | 0,76 | 1102,15 | 33,867 | 1146,974 | 8028,816 | |||
| 168,1 | 178,75 | 0,1 | 0,86 | 1787,5 | 55,167 | 3043,398 | 30433,98 | |||
| 189,4 | 200,05 | 0,04 | 0,9 | 800,2 | 76,467 | 5847,202 | 23388,81 | |||
| 210,7 | 221,35 | 0,1 | 2213,5 | 97,767 | 9558,386 | 95583,86 | ||||
| Сумма | 12358,3 |
Таблица 3
| № интервала | 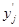
| 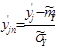
| 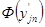
| 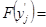
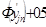
| 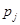
| 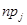
| 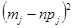
| 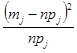
|
| -1,89849 | -0,4713 | 0,0287 | 0,0368 | 3,68 | 8,4681 | 0,421508 | ||
| 40,3 | -1,51183 | -0,4345 | 0,0655 | 0,0659 | 6,59 | |||
| 61,6 | -1,12517 | -0,3686 | 0,1314 | 0,0982 | 9,82 | |||
| 82,9 | -0,73852 | -0,2704 | 0,2296 | 0,1336 | 13,36 | 11,2896 | 0,84503 | |
| 104,2 | -0,35186 | -0,1368 | 0,3632 | 0,1488 | 14,88 | 123,6544 | 8,310108 | |
| 125,5 | 0,034799 | 0,012 | 0,512 | 0,1508 | 15,08 | 25,8064 | 1,7113 | |
| 146,8 | 0,421457 | 0,1628 | 0,6628 | 0,1282 | 12,82 | 33,8724 | 2,642153 | |
| 168,1 | 0,808114 | 0,291 | 0,791 | 0,092 | 9,2 | 30,6916 | 1,6626 | |
| 189,4 | 1,194772 | 0,383 | 0,883 | 0,0599 | 5,99 | |||
| 210,7 | 1,58143 | 0,4429 | 0,9429 | 0,0327 | 3,27 | |||
| 1,968087 | 0,4756 | 0,9756 | ||||||
| Сумма | 13,5927 |
| <== предыдущая | | | следующая ==> |
| Допоміжна. Балабанова Л.В. Стратегічне маркетингове управління конкурентоспроможністю підприємств: навч | | | Сущность менеджмента |
Date: 2015-07-25; view: 335; Нарушение авторских прав