
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Виды дисперсий и правило их сложения
|
|
Всякая совокупность, состоящая из значительного числа единиц, может быть расчленена по тому или иному признаку на части, которые называют частными совокупностям или группами.
Совокупность, состоящую из нескольких групп, называют общей.
Для общей и частной совокупностей могут быть определены средние величины и дисперсии, которые соответственно называются общими и групповыми.

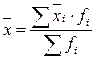 ,
,
где 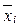 - групповая средняя;
- групповая средняя;
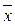 - общая средняя;
- общая средняя;
х - индивидуальные значения признака;
f - число единиц, обладающих данным значением признака;
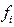 - численность единиц в группе.
- численность единиц в группе.
Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней 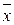 .
.
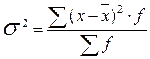
Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней).
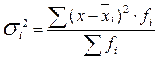
Групповая дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы.
Средняя из групповых (частных) дисперсий - это средняя взвешенная из групповых дисперсий (или остаточная):
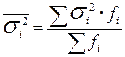 .
.
Средняя из групповых дисперсий не равна общей дисперсии, т.к. она не учитывает колеблемости признака между группами.
Поскольку групповые средние (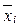 ) являются варьирующей величиной, то может быть определена их дисперсия.
) являются варьирующей величиной, то может быть определена их дисперсия.
Межгрупповая дисперсия характеризует вариацию результативного признака за счет группировочного признака. Она равна среднему квадрату отклонений групповых средних (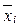 ) от общей средней (
) от общей средней (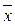 )
)
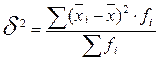 .
.
Между общей, средней из групповых и межгрупповой дисперсиями существует следующая зависимость:
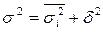 , т.е. общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это соотношение называют правилом сложения дисперсий.
, т.е. общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это соотношение называют правилом сложения дисперсий.
Достоверность правила сложения дисперсий покажем на примере.
Имеются следующие данные о выполнении норм выработки рабочими участка:
| Группы рабочих | Выполнение норм выработки, % | ||||||||
| до | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 | и выше | Итого | |
| Окончившие ПТУ Не прошедшие обучение | - | - | - | ||||||
| Итого |
Для расчета средних величин и дисперсий используем способ «моментов»(см. табл.3).
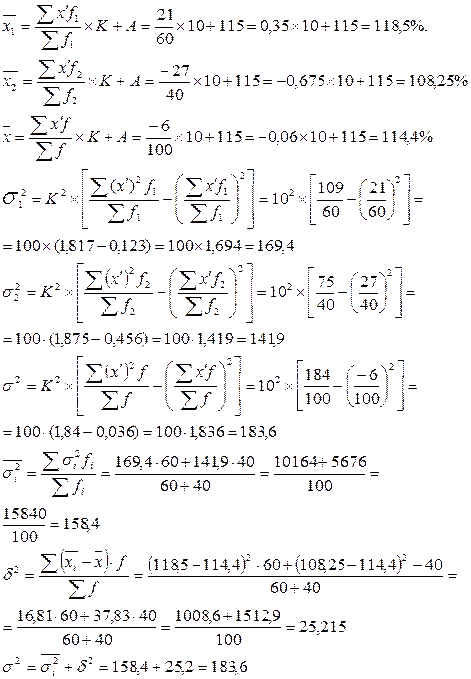
Таблица 3
Расчетная таблица
| Выполнение норм выработки, % | Серединное
значение, (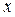 ) )
| Число рабочих | х-А А =115 | x-A K K=10 (х’) | 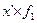
| 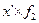
| 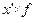
| 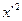
| 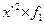
| 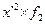
| 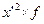
| ||
Окончивших ПТУ
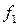
| Не прошедших обучение
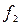
| всего

| |||||||||||
| до 90 90-100 100-110 110-120 120-130 130-140 140-150 150 и более | - | - - | -30 -20 -10 +10 +20 +30 +40 | -3 -2 -1 +1 +2 +3 +4 | -4 -14 +11 +12 +12 +4 | -9 -10 -16 +4 +4 | -9 -14 -30 +15 +16 +12 +4 | ||||||
| Итого | -27 | -6 |
Тема: ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Date: 2015-07-24; view: 464; Нарушение авторских прав