Приклади розв’язання завдань для самостійної роботи з вищої математики

Частина VІ

Диференціальні рівняння

Методичні вказівки для студентів технічних спеціальностей

КІРОВОГРАД

Приклади розв’язання завдань для самостійної роботи з вищої математики. Частина VІ. Диференціальні рівняння. Методичні вказівки для студентів технічних спеціальностей/ Укл.: Гончарова С.Я. – Кіровоград: КНТУ, 2015.– 49 с.

Методичні вказівки містять приклади розв’язання завдань для самостійної роботи за темою «Диференціальні рівняння».

Затверджено на засіданні

кафедри вищої математики.

Протокол № 8 від 16/04/2015 р.

Завдання 1. Розв’язати диференціальні рівняння першого порядку:

а) ;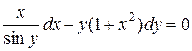

Розв’язок. Розділимо змінні:

.

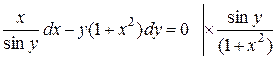Отримаємо рівняння з розділеними змінними

.

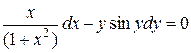Інтегруючи, знаходимо:

,

,

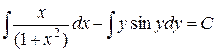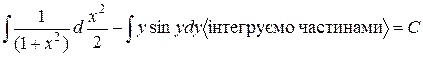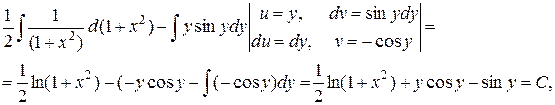
тобто

.

Останнє співвідношення є загальним інтегралом даного рівняння.

Перевірка.

Отриманий загальний інтеграл рівняння

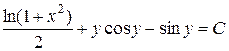
– неявно задана функція 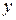від .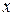

Знайдемо похідну 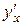, використавши формулу для неявно заданої функції :

.

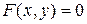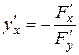Таким чином,

,

.

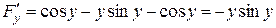Отримаємо:

.

Початкове рівняння перепишемо у вигляді

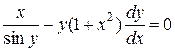
і підставимо отриману похідну:

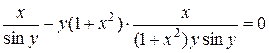
або

.

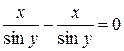Отже, рівняння розв’язане правильно t.

б) ;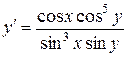

Розв’язок. Розділимо змінні:

.

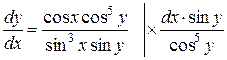Отримаємо рівняння з розділеними змінними

.

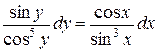Інтегруючи, знаходимо:

,

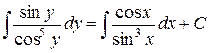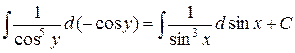
або

.

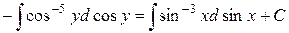Звідки

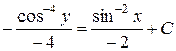
або

.

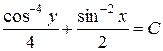Останнє співвідношення є загальним інтегралом даного рівняння.

Перевірка.

Отриманий загальний інтеграл рівняння

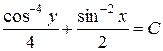
– неявно задана функція 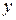від .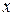

Знайдемо похідну 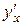як похідну неявно заданої функції :

,

.

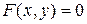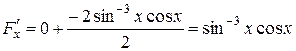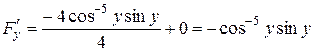Отримаємо:

.

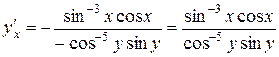Підставимо отриману похідну в початкове рівняння:

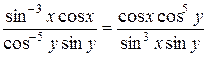
або

.

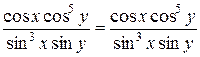Отже, рівняння розв’язане правильно t.

в) ;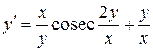

Розв’язок. Дане рівняння є рівнянням першого порядку вигляду 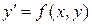і є однорідним рівнянням відносно 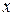та 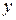, так як функція 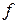залежить тільки від відношення 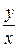, тобто

.

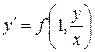Зробимо заміну 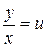, тоді

, .

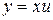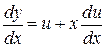Отримаємо:

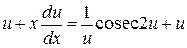
або

.

Розділимо змінні:

.

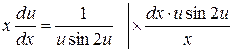Отримаємо рівняння з розділеними змінними

.

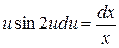Інтегруючи, знаходимо:

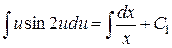
або

.

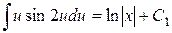Первісну зліва знайдемо, застосовуючи формулу інтегрування частинами, а саме,

.

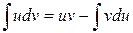Отримаємо:

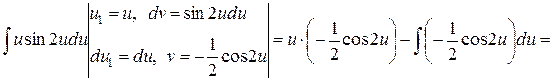
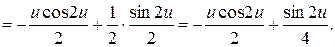
Таким чином

.

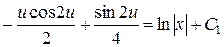Підставивши 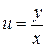, отримаємо загальний інтеграл початкового рівняння:

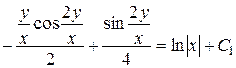
або

.

Звідки

.

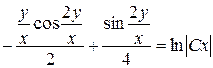Перевірка.

Отриманий загальний інтеграл рівняння

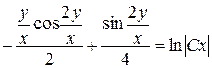
– неявно задана функція 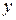від .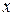

Знайдемо похідну 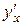як похідну неявно заданої функції :

.

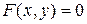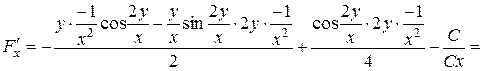
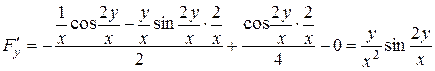Отримаємо:

.

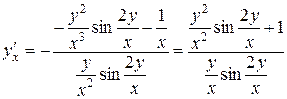Підставимо отриману похідну в початкове рівняння:

або

.

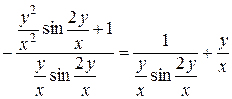Зведемо праву частину до спільного знаменника:

.

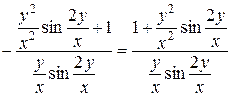Отже, рівняння розв’язане правильно t.

г) ;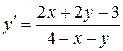

Розв’язок. Дане рівняння є рівнянням першого порядку вигляду

.

Можливі два випадки:

1) якщо 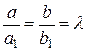, то рівняння зводиться до рівняння з розділюваними змінними;

2) якщо , то рівняння приводиться до однорідного рівняння.

Так як

,

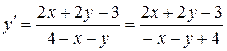то 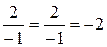, то дане рівняння зводиться до рівняння з розділюваними змінними.

Підберемо заміну змінних:

,

тоді

, ,

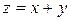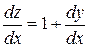звідки

.

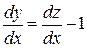Після підстановки, отримаємо

,

,

,

.

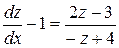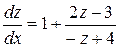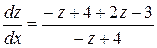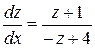Розділимо змінні:

.

Отримаємо рівняння з розділеними змінними

.

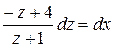Інтегруючи, знаходимо:

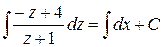
або

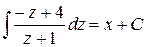
Знайдемо первісну зліва:

.

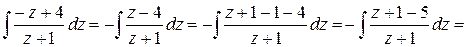
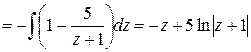Таким чином,

або

.

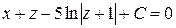Підставивши 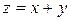, отримаємо загальний інтеграл початкового рівняння

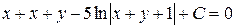
або

.

Перевірка.

Отриманий загальний інтеграл рівняння

– неявно задана функція 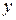від .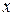

Знайдемо похідну 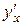як похідну неявно заданої функції :

,

.

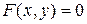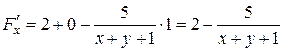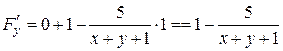Отримаємо:

.

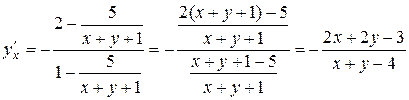Підставимо отриману похідну в початкове рівняння:

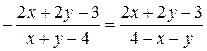
або

.

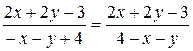Отже, рівняння розв’язане правильно t.

д) ;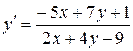

Розв’язок. Дане рівняння є рівнянням першого порядку вигляду

,

що зводиться до однорідного, так як

.

Щоб привести його до однорідного рівняння, робимо заміну:

, , , .

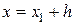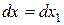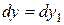Звідки

.

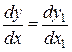Тоді

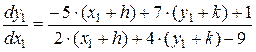
або

.

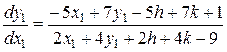Підберемо 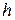і 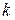, так, щоб виконувались рівності:

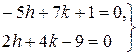
або

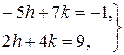
тобто визначимо 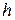і 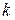як розв’язок системи.

Розв’язуючи систему двох рівнянь за методом Крамера, знаходимо

,

.

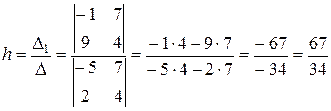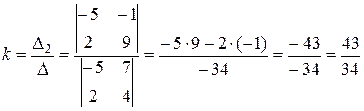При цій умові останнє рівняння стає однорідним:

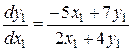
або

,

.

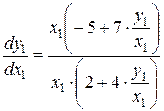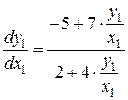Розв’язуємо його підстановкою:

,

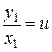тоді

, ,

.

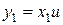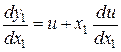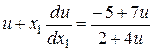Отримане рівняння є рівнянням з розділюваними змінними:

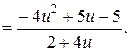
Розділимо змінні:

.

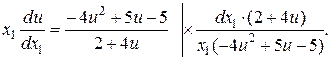Отримаємо рівняння з розділеними змінними

.

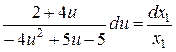Інтегруючи, знаходимо:

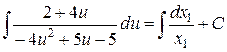
або

.

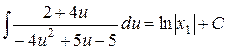Знайдемо первісну зліва:

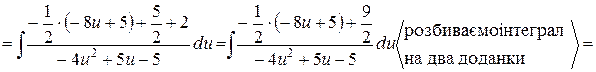
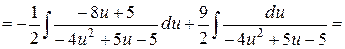
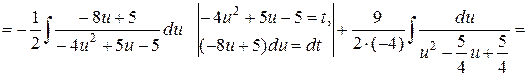
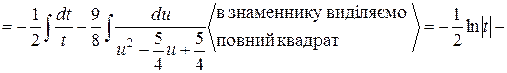
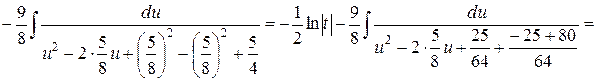
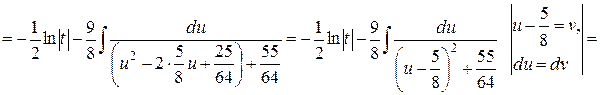
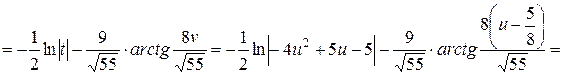
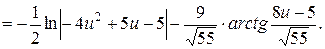
Таким чином,

.

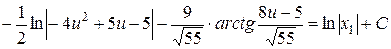Підставивши 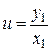, отримаємо:

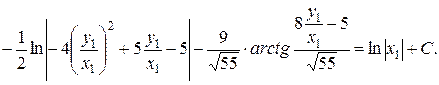
Перейдемо до змінних 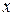та :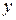

, ;

, .

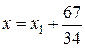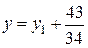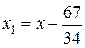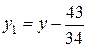Отримаємо

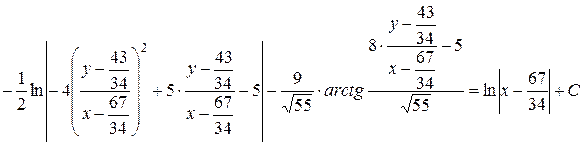
або

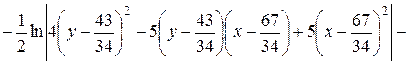
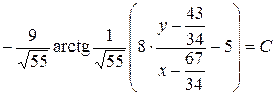
– це співвідношення є загальним інтегралом даного рівняння t.

е) .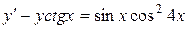

Розв’язок. Дане рівняння є рівнянням вигляду

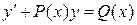
і є лінійним рівнянням першого порядку відносно невідомої функції 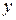та її похідної .

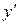Шукатимемо розв’язок даного рівняння у вигляді добутку двох функцій від :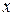

,

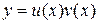тоді

.

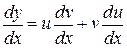Зробивши підстановку в дане рівняння, отримаємо

,

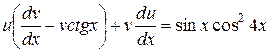(1)

Виберемо функцію 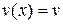так, щоб

.

Розділимо змінні:

.

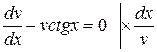Отримаємо рівняння з розділеними змінними

.

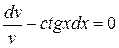Інтегруючи, знаходимо:

,

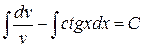візьмемо .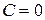

Звідки

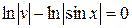
або

.

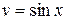Підставивши вираз для функції 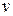в рівняння (1), отримаємо рівняння для знаходження функції :

,

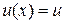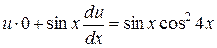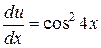
або

.

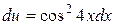Інтегруючи, знаходимо:

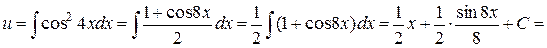
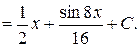
Таким чином, загальний розв’язок заданого рівняння матиме вигляд

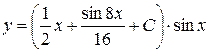
або

.

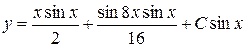Перевірка.

.

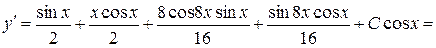
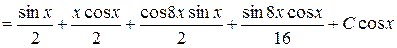Підставимо 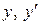в початкове рівняння:

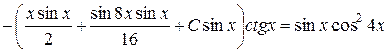
або

,

,

,

,

.

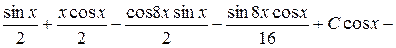
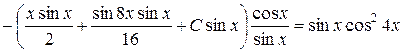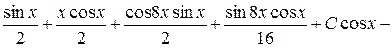
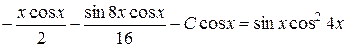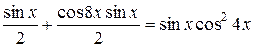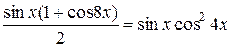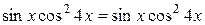Отже, рівняння розв’язане правильно t.

Завдання 2. Розв’язати задачу Коші:

, .

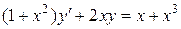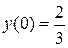Розв’язок.

,

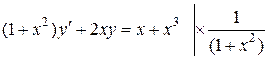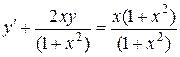
або

.

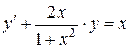Дане рівняння є лінійним рівнянням першого порядку відносно невідомої функції 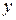та її похідної .

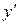Шукатимемо його розв’язок у вигляді добутку

,

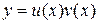тоді

.

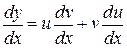Зробимо підстановку в отримане рівняння:

.

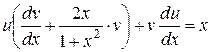. (2)

Виберемо функцію 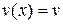так, щоб

.

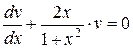Розділимо змінні:

,

.

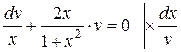Інтегруючи, знаходимо:

,

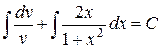візьмемо .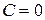

Звідки

,

.

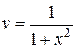Підставивши вираз для функції 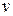в рівняння (2), отримаємо рівняння для знаходження функції :

.

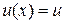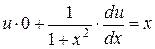Розділимо змінні:

,

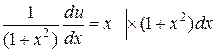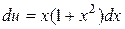
Інтегруючи, знаходимо:

.

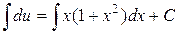Звідки

.

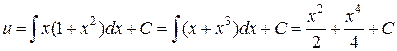Таким чином, загальний розв’язок заданого рівняння матиме вигляд

.

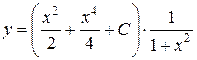Знайдемо частинний розв’язок, що задовольняє початковій умові :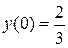

.

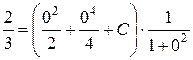Звідки

.

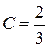Отримаємо розв’язок задачі Коші

.

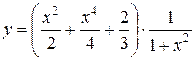Перевірка.

.

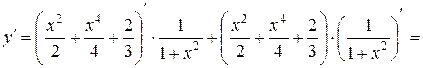
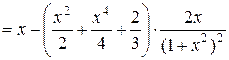Підставимо 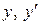в початкове рівняння:

,

,

.

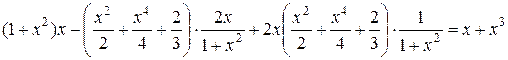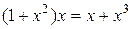Отже, рівняння розв’язане правильно t.

Завдання 3. Розв’язати рівняння Бернуллі:

.

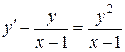Розв’язок. Дане рівняння є рівнянням вигляду

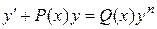
і є рівнянням Бернуллі, що зводиться до лінійного рівняння першого порядку.

Розділивши всі члени рівняння на 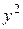, отримаємо:

.

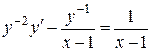Зробимо заміну:

, .

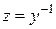Зробивши підстановку, отримаємо:

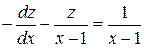
або

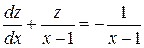
– лінійне рівняння першого порядку.

Шукатимемо його розв’язок у вигляді добутку

,

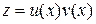тоді

.

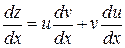Зробимо підстановку в отримане рівняння:

.

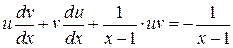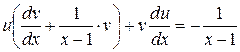. (3)

Виберемо функцію 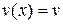так, щоб

.

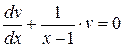Розділимо змінні:

,

.

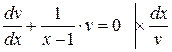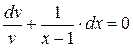Інтегруючи, знаходимо:

,

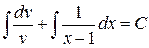візьмемо .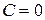

Звідки

,

,

.

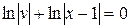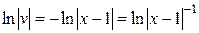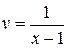Підставивши вираз для функції 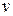в рівняння (3), отримаємо рівняння для знаходження функції :

,

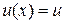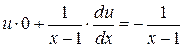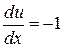
або

.

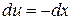Інтегруючи, знаходимо:

,

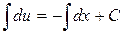тобто

.

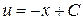Таким чином,

,

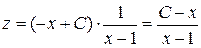тобто

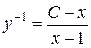
або

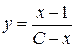
– загальний розв’язок заданого рівняння.

Перевірка.

.

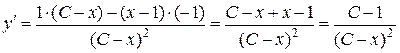Підставимо 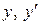в початкове рівняння:

,

,

,

.

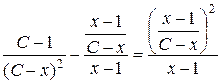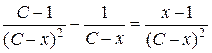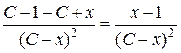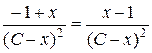Отже, рівняння розв’язане правильно t.

Завдання 4. Розв’язати рівняння в повних диференціалах:

.

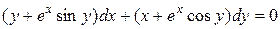Розв’язок. Дане рівняння є рівнянням вигляду

.

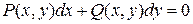Якщо в ньому

,

то ліва частина такого рівняння є повним диференціалом деякої функції 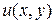і рівняння є рівнянням в повних диференціалах. Якщо це рівняння переписати у вигляді 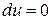, то його загальний розв’язок визначається рівністю .

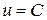Тут

, ;

, .

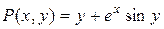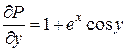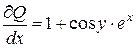Отже, ліва частина даного рівняння є повним диференціалом деякої функції 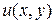, тобто

, .

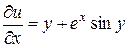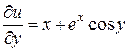1 спосіб.

Інтегруєм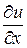о по :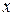

.

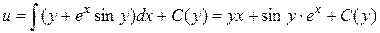Знайдемо функцію 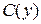, диференціюючи останній вираз по :

.

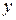Отримуємо рівняння

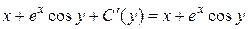
або

,

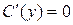тобто

.

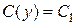Таким чином,

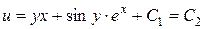
і загальний інтеграл рівняння має вигляд

,

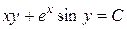де 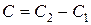t.

2 спосіб.

Функція 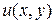може бути знайдена за формулою

,

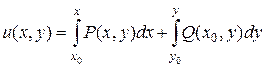де 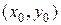– довільна точка.

Знайдемо функцію 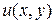за цією формулою, взявши , :

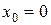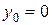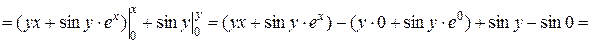
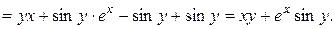
Таким чином, загальний інтеграл рівняння рівний

.

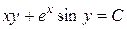Перевірка.

Отриманий загальний інтеграл рівняння

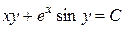
– неявно задана функція 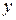від .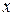

Знайдемо похідну 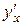як похідну неявно заданої функції :

,

.

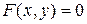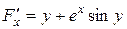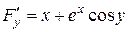Отримаємо:

.

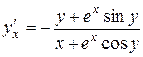Початкове рівняння перепишемо у вигляді

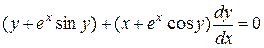
і підставимо отриману похідну:

,

.

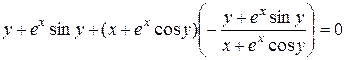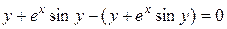Отже, рівняння розв’язане правильно t.

Завдання 5. Розв’язати диференціальні рівняння вищих порядків:

а) ;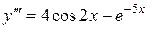

Розв’язок. Дане рівняння є рівнянням третього порядку вигляду

,

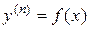де .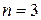

Знайдемо загальний інтеграл цього рівняння.

Інтегруючи по 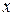ліву і праву частини і приймаючи до уваги, що

,

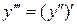отримаємо:

.

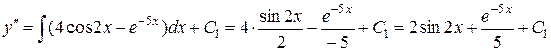Інтегруючи ще раз, отримаємо:

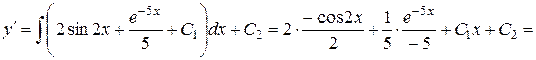
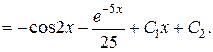
Продовживши інтегрування, отримаємо загальний розв’язок рівняння:

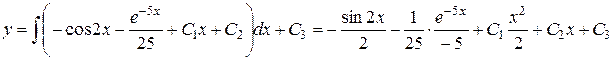
або

.

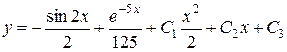Перевірка.

,

,

.

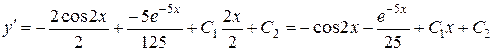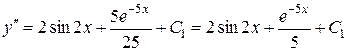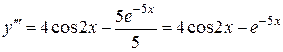Підставимо похідну 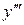в початкове рівняння:

.

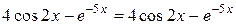Отже, рівняння розв’язане правильно t.

б) ;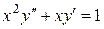

Розв’язок. Дане рівняння є рівнянням другого порядку вигляду

,

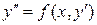яке не містить у явному вигляді шуканої функції 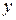. Для його розв’язку покладемо

.

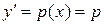Тоді

.

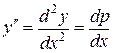Підставляючи в дане рівняння вирази для 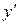і 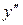, отримаємо рівняння першого порядку відносно допоміжної функції :

,

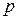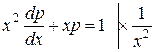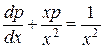
або

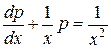
– лінійне рівняння першого порядку.

Шукатимемо його розв’язок у вигляді добутку

,

.

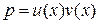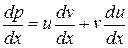Зробимо підстановку в отримане рівняння:

.

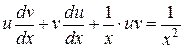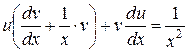. (4)

Виберемо функцію 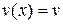так, щоб

.

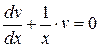Розділимо змінні:

,

.

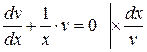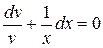Інтегруючи, знаходимо:

,

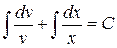візьмемо .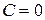

Звідки

,

,

.

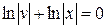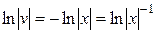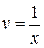Підставивши вираз для функції 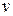в рівняння (4), отримаємо рівняння для знаходження функції :

,

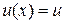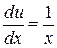
або

.

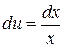Інтегруючи, знаходимо:

,

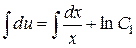тобто

.

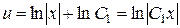Таким чином,

.

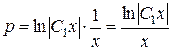Так як 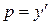, то

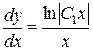
або

.

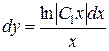Інтегруючи, знаходимо шукану функцію :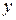

,

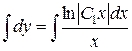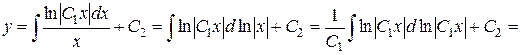
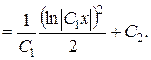
Таким чином

– загальний розв’язок даного рівняння t.

в) .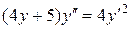

Розв’язок. Дане рівняння є рівнянням другого порядку вигляду

,

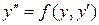яке не містить у явному вигляді незалежної змінної 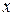. Для його розв’язку покладемо

.

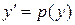Тоді

.

Підставляючи в дане рівняння вирази для 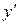і 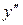, отримаємо рівняння першого порядку відносно допоміжної функції :

,

,

,

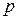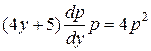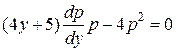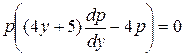тобто:

1) 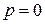, тобт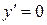о або 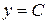– перший загальний розв’язок даного рівняння;

2) .

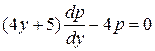Інтегруючи отримане рівняння, найдемо 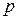як функцію від 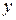і довільної константи :

,

,

,

,

,

.

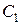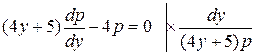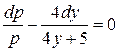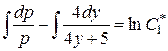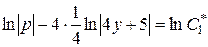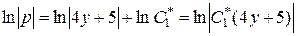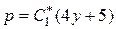Так як 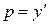, то для визначення 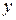отримуємо рівняння

,

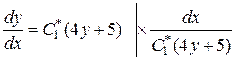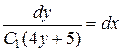
або

.

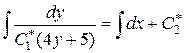Отримаємо:

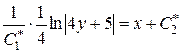
– другий загальний інтеграл даного рівняння.

Таким чином, загальним інтегралом даного рівняння є множина розв’язків

,

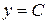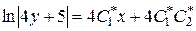
або

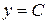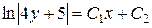, t.

Завдання 6. Розв’язати неоднорідні лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами:

а) ;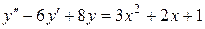

Розв’язок. Характеристичне рівняння

,

.

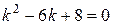Його корені

,

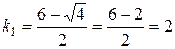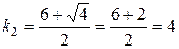
– дійсні і різні, тому загальний розв’язок однорідного рівняння матиме вигляд

,

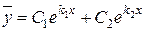тобто

.

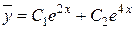Права частина даного рівняння рівна

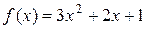
і має вигляд 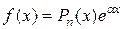при і 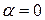, до того ж коефіцієнт 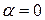в показникові степеня не є коренем характеристичного рівняння. Тому частинний розв’язок шукатимемо у вигляді

.

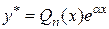В даному випадку і 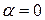, тобто

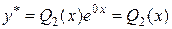
або

.

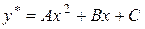Отже,

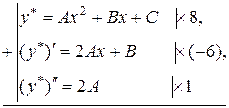
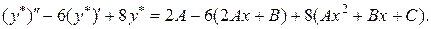
Таким чином,

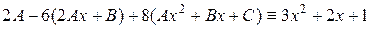
або

.

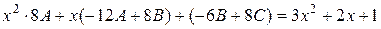Прирівнюючи коефіцієнти при однакових степенях 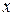, що стоять в різних частинах рівності, отримаємо систему з трьох рівнянь для знаходження невідомих констант, а саме

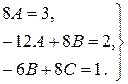
Звідки

;

, , ;

, , .

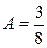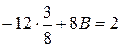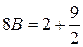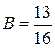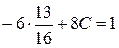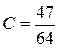Отже, частинний розв’язок

.

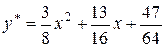Таким чином, загальний розв’язок початкового рівняння рівний

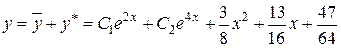t.

б) ;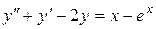

Розв’язок. Характеристичне рівняння

,

.

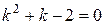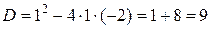Його корені

, .

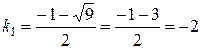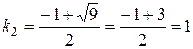Тому загальний розв’язок однорідного рівняння

.

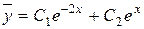Права частина даного рівняння рівна

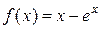
і є сумою двох доданків 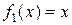та 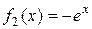, кожний з яких має вигляд 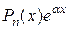, при цьому

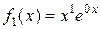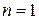, і 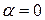не є коренем характеристичного рівняння;

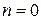, і 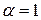є простим коренем характеристичного рівняння.

Щоб знайти частинний розв’язок даного рівняння треба використати принцип накладання розв’язків: знайти частинні розв’язки, що відповідають окремим доданкам правої частини, та взяти їх суму, яка і є частинним розв’язком початкового рівняння.

Частинний розв’язок 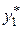, що відповідає 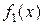, шукатимемо у вигляді 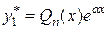. В даному випадку 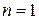і 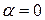, тобто .

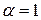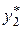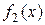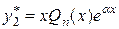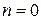Так як коефіцієнт є простим коренем характеристичного рівняння, то частинний розв’язок , що відповідає , шукатимемо у вигляді при і 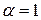, тобто

.

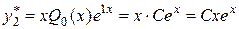Таким чином, частинний розв’язок даного рівняння

.

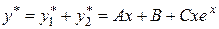Отже,

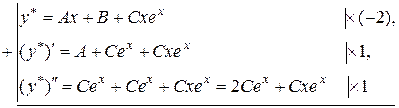
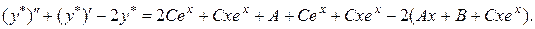
Таким чином,

,

,

.

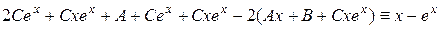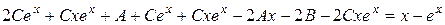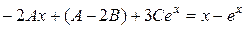Прирівнюючи відповідні коефіцієнти, що стоять в різних частинах рівності, отримаємо систему з трьох рівнянь для знаходження невідомих констант, а саме

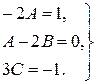
Звідки

;

, , ;

.

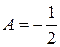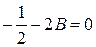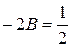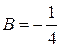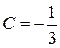Отже, частинний розв’язок

.

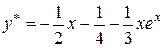Таким чином, загальний розв’язок початкового рівняння рівний

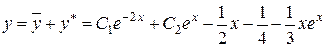t.

в) ;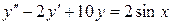

Розв’язок. Характеристичне рівняння

,

.

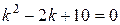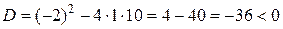Його корені

,

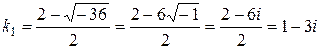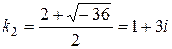
– комплексні, тому загальний розв’язок однорідного рівняння матиме вигляд

.

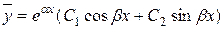Тут 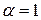, , 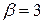отже

.

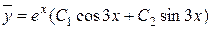Права частина даного рівняння рівна

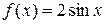
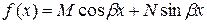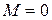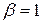і має вигляд при , та 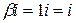не є коренем характеристичного рівняння. Тому частинний розв’язок шукатимемо у вигляді

,

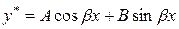в даному випадку

.

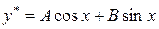Отже,

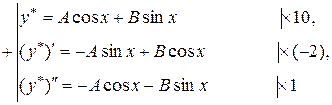
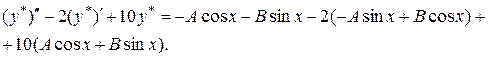
Таким чином,

,

,

.

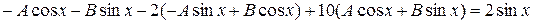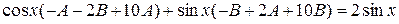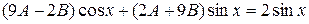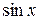Прирівнюючи коефіцієнти при і при , отримаємо систему з двох рівнянь для знаходження невідомих констант, а саме

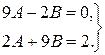
Звідки

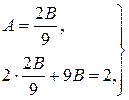
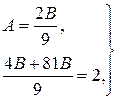
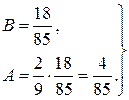
Отже, частинний розв’язок

.

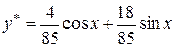Таким чином, загальний розв’язок початкового рівняння рівний

.

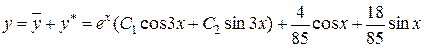Перевірка.

,

.

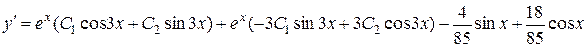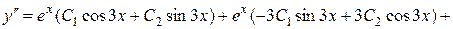
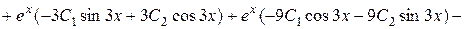
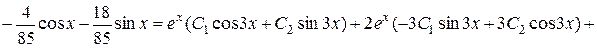
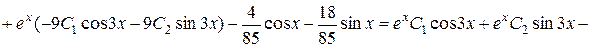
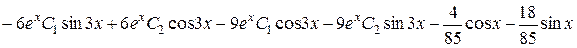Підставимо 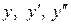в початкове рівняння:

,

,

,

,

.

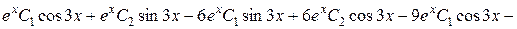
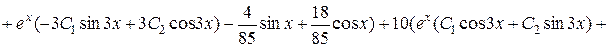
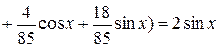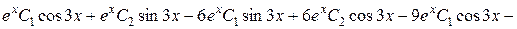
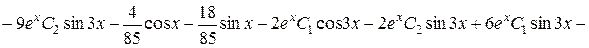
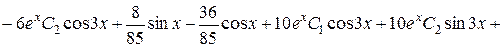
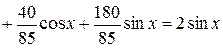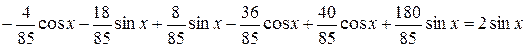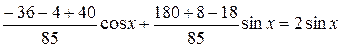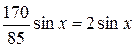Отже, рівняння розв’язане правильно t.

г) ;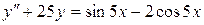

Розв’язок. Характеристичне рівняння

,

.

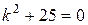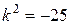Його корені

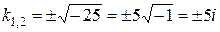
– комплексні, тому загальний розв’язок однорідного рівняння матиме вигляд

.

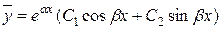Тут 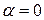, , 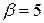отже

.

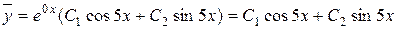Права частина даного рівняння рівна

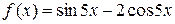
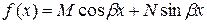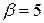і має вигляд при та 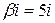є коренем характеристичного рівняння. Тому частинний розв’язок шукатимемо у вигляді

,

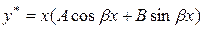в даному випадку

.

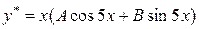Отже,

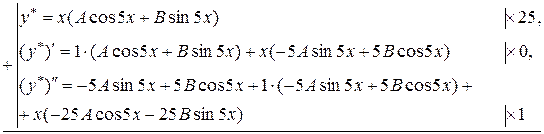
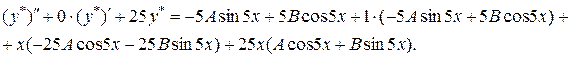
Таким чином,

,

.

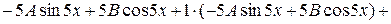
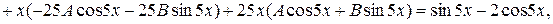
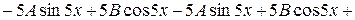
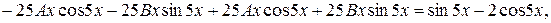
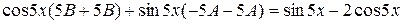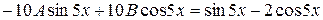Прирівнюючи коефіцієнти 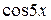при і при 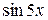, отримаємо систему з двох рівнянь для знаходження невідомих констант, а саме

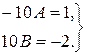
Звідки

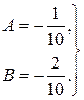
Отже, частинний розв’язок

.

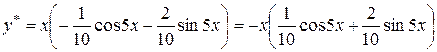Таким чином, загальний розв’язок початкового рівняння рівний

.

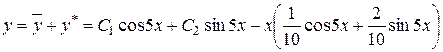Перевірка.

,

.

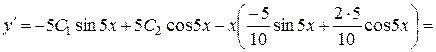
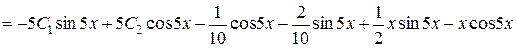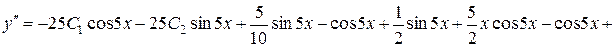
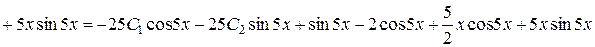Підставимо 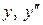в початкове рівняння:

,

,

.

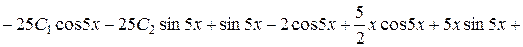
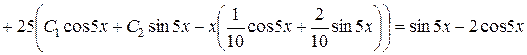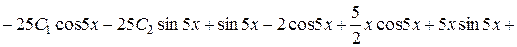
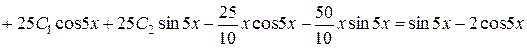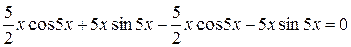Отже, рівняння розв’язане правильно t.

д) ;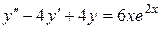

Розв’язок. Характеристичне рівняння

,

.

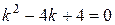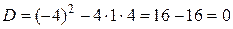Його корені

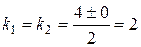
– дійсні і рівні, тому загальний розв’язок однорідного рівняння матиме вигляд

,

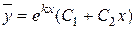тобто

.

Права частина даного рівняння рівна

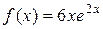
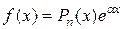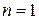і має вигляд при і 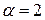, до того ж коефіцієнт 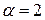в показникові степеня є двократним коренем характеристичного рівняння. Тому частинний розв’язок шукатимемо у вигляді

.

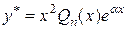В даному випадку 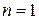і 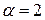, тобто

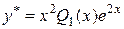
або

.

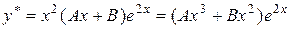Отже,

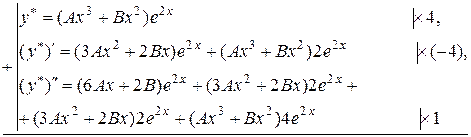
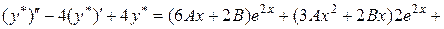
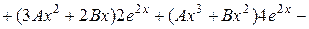
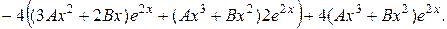
Таким чином,

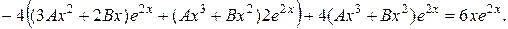
Скоротивши на 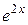, отримаємо:

.

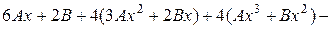
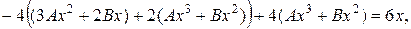
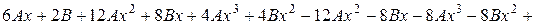
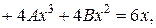
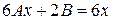Прирівнюючи коефіцієнти при однакових степенях 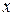, що стоять в різних частинах рівності, отримаємо систему з двох рівнянь для знаходження невідомих констант, а саме

Date: 2015-07-24; view: 534; Нарушение авторских прав