Теоретичні відомості. Принцип невизначеностей Гейзенберга для координати та імпульсу частинки

Принцип невизначеностей Гейзенберга для координати та імпульсу частинки. У класичній механіці стан матеріальної точки в кожний момент часу характеризується її положенням і імпульсом. Реальні мікрочастинки - електрони, протони, атоми та інші - більш складні об'єкти. Не можна характеризувати миттєвий стан мікрочастинки точними завданнями її положення й імпульсу. Причина цього полягає у тому, що будь-яка мікрочастинка виявляє і корпускулярні і хвильові властивості. Не можна сказати, що у певній точці простору довжина хвилі дорівнює 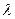, оскільки довжина хвилі є характеристика синусоїди, а це є періодична крива.

З іншого боку, якщо будь-яке хвильове утворення займає обмежену область простору, то його завжди можна представити синусоїдами. Тільки однієї синусоїди для цього недостатньо. Потрібен хвильовий пакет - суперпозиція безлічі синусоїд різних частот, що підсилювалися б у певному інтервалі простору ∆ х і взаємно гасили би один одного поза цим інтервалом. Якщо довжина хвильового пакета - ∆ х, то хвильові числа k, необхідні для його утворення, не можуть займати який завгодно вузький інтервал. Мінімальна ширина інтервалу повинна задовольняти умові:

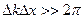. (5.1)

Це абсолютно хвильове співвідношення.

Виражаючи 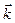через 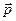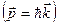, співвідношення (5.1) можна переписати у вигляді:

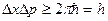. (5.2)

Але його не можна тлумачити таким чином, що частинка в кожен момент часу має певні значення х і р, але ми їх не можемо визначити з більшою точністю, ніж це дозволяє співвідношення невизначеностей. Зміст співвідношення (5.2) відбиває той факт, що у природі об'єктивно не існує стану частинок з точно визначеними значеннями х і р.

Співвідношення (5.2) проявляється при всякій спробі виміру точного положення чи точного імпульсу частинки. Виявляється, що уточнення положення частинки позначається на збільшенні неточності в значенні імпульсу, і навпаки. Перевірці цього співвідношення і присвячується дана робота.

Співвідношення невизначеностей для фотонів. Нехай рух фотона описується плоскою монохроматичною хвилею де Бройля 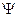. Фотон у такому стані має цілком визначений імпульс:

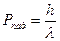, (5.3)

але його координата зовсім не визначена. Для визначення x -координати фотона на шляху поширення хвилі ставиться непрозорий екран із щілиною шириною 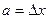. Якщо фотон пройшов через щілину, то в площині самої щілини координата x буде зафіксована з точністю 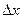~ a. Однак після проходження щілини в результаті дифракції хвильова функція фотона 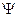зміниться. Вона буде мати максимуми і мінімуми (рис. 5.1). Фотон може бути виявлений у будь-якому місці, де 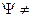0. Як видно з рис. 5.1, практично усе хвильове поле буде зосереджено у межах центрального максимуму. Його кутова ширина дорівнює 2 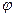(рис.5.2), а умова максимуму відповідно має вигляд:

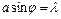. (5.4)

Враховуючи, що випромінювання розповсюджується як на кути більше 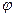, так і на кути менше 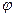, можна записати наступну хвильову умову невизначеності, якій підкоряються кути для більшої частини плоских хвиль, розсіяних на щілині:

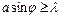. (5.4 а)

З формули (5.4 а) випливає, що звуження щілини (а) обов'язково супроводжується розширенням сектору напрямку (sin 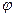), в якому зосереджено дифракційне поле. Як видно з рис. 5.1, при збільшенні ширини щілини вдвічі, тобто при а ₂ = 2 а ₁, інтервал значень sin φ, що відповідає центральному максимуму, скорочується вдвічі.

Після проходження через щілину у фотона з'являється x -компонента імпульсу (рис. 5.2):

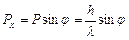. (5.5)

Для фотонів, що відхиляються на різні кути, як менше φ, так і більше φ, значення 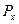різні. В цьому випадку вираз (5.4 а) з урахуванням (5.5) запишеться у вигляді:

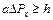
чи 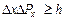, (5.6)

- де 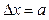- область локалізації (невизначеність

місцеположення) фотонів в площині екрану;

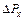- область значень (невизначеність) компонент

імпульсу.

x

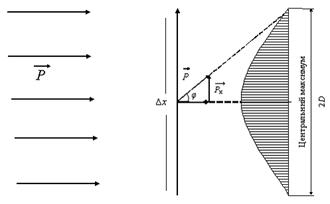
Рис. 5.2. Схема проходження фотонів через щілину

Співвідношення (5.6) показує, що добуток невизначеності координати на невизначеність відповідного їй імпульсу має величину порядку h= 6,62·10^-34 Дж∙с. Чим точніше визначена одна з цих величин, наприклад чим вужче щілина, через яку проходять фотони, тим більш невизначеним стає імпульс Р_х, і, навпаки, чим ширше щілина (Dх®¥), тим більш визначений імпульс (DР_х® 0). Очевидно, якщо одна з величин має цілком певне значення, то інша є абсолютно невизначеною.

Перевіримо співвідношення невизначеностей (5.6) за допомогою експерименту. Для цього будемо вимірювати ширину щілини, яка характеризує невизначеність координати фотона, і ширину дифракційної картини, яка характеризує невизначеність поперечної координати імпульсу фотона DР_x.

Date: 2015-07-24; view: 479; Нарушение авторских прав