Теорема Гаусса в дифференциальной форме

ЛЕКЦИЯ №44

С помощью интегральной теоремы Гаусса нельзя определить, как связан исток линий 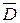в данной точке поля с плотностью свободных зарядов в той же точке поля. Поэтому переходят к записи теоремы Гаусса в дифференциальной форме:

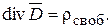(15.16)

Исток линий 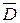в данной точке поля определяется величиной плотности свободных зарядов в этой точке (рис. 15.4).

Если среда однородна и изотропна, т.е. e_a = const, то можно записать:

(15.17)

или:

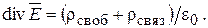(15.18)

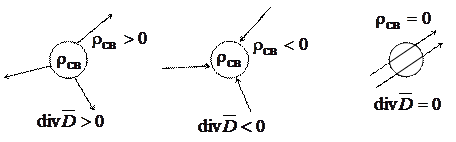Рис. 15.4. К пояснению истока линий вектора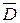

Истоком вектора 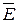в отличие от истока вектора 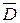являются не только свободные, но и связанные заряды.

С другой стороны известно, что

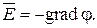
С учетом этого

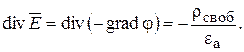
Или

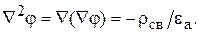(15.19)

Уравнение (15.19) называется уравнением Пуассона. Частный вид уравнения Пуассона при r_св = 0, называется уравнением Лапласа

.

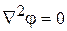Эти два уравнения являются основными уравнениями электростатики. Уравнение Пуассона выражает связь между частными производными второго порядка от j в любой точке поля и плотностью свободных зарядов в этой точке поля.

Решение уравнения Пуассона в общем виде можно найти следующим образом. Положим, что в объеме V есть объемные r, поверхностные s и линейные t заряды. Эти заряды представим в виде совокупности точечных зарядов: r dV, s ds и t dl, где dV – элемент объема, ds – элемент заряженной поверхности, dl – элемент длинны заряженной оси. Составляющая потенциала d j в некоторой точке пространства, удаленной от r dV на расстояние r, в соответствии с формулой (15.15) равна

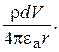
Аналогично можно определить составляющие потенциала от поверхностного и линейного зарядов

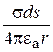и .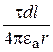

Полное значение j определяется как сумма (интеграл) составляющих потенциала от всех зарядов поля:

(15.20)

В формуле (15.20) r, s и t есть функции радиуса r, которые практически определить очень трудно. Предполагается, что потенциал на бесконечности равен нулю и заряды, создающие поля распределены в ограниченной области (иначе интеграл может оказаться расходящимся).

Date: 2015-07-24; view: 444; Нарушение авторских прав