Теорема Гаусса в интегральной форме

Формулируется тремя способами:

1. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности

(15.11)

Вектор 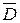– это такая характеристика поля, которая не зависит от диэлектрических свойств среды.

2. Так как 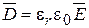, то теорему Гаусса для однородной и изотропной среды можно записать:

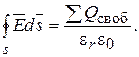(15.12)

Вектор 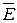– это характеристика поля, которая зависит от диэлектрических свойств среды.

3. Поток вектора 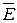через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов

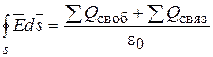. (15.13)

Теорему Гаусса можно использовать для нахождения напряженности или электрического смещения в какой-либо точке поля, если через эту точку можно провести замкнутую поверхность таким образом, что все ее точки будут в симметричных (одинаковых условиях по отношению к заряду, находящемуся внутри замкнутой поверхности).

Такой поверхностью являются обычно сфера (если заряд точечный), или боковая поверхность цилиндра (если заряд линейный).

В качестве примера использования теоремы Гаусса найдем напряженность поля, создаваемую точечным зарядом в точке, удаленной на расстояние r от заряда. С этой целью через заданную точку проведем сферическую поверхность радиусом r, полагая, что заряд находится в центре сферы (рис. 15.3).

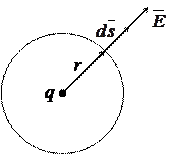Рис. 15.3. К определению поля точечного заряда

Элемент поверхности сферы 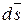перпендикулярен поверхности сферы и направлен в сторону внешней нормали, т.е. векторы 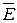и 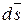в каждой точке сферы совпадают по направлению

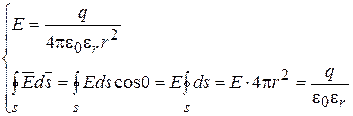(15.14)

Напряженность поля:

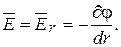
Откуда

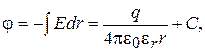(15.15)

где C – постоянная интегрирования.

Date: 2015-07-24; view: 711; Нарушение авторских прав