
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интегральные теоремы
|
|
ЛЕКЦИЯ №42
Теоремы Остроградского-Гауса и Стокса применяют при переходе от уравнений поля, записанных в интегральной форме, к уравнениям поля в дифференциальной форме и наоборот.
Таблица 14.1
| Векторная операция | Символическая запись с помощью оператора Ñ | Примечание |
| grad j | Ñj | |
div 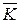
| Ñ 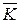
| |
rot 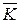
| Ñ´ 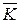
| jÑ 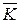 + + 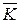 Ñj=j×div Ñj=j×div 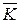 + + 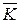 ×grad j ×grad j
|
div j 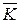
| Ñ(Ñj) | |
| div grad j | Ñ(Ñj) = Ñ2j
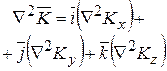
| |

| 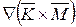
| 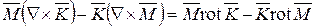
|
div rot 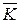
| Ñ(Ñ´ 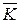 ) = 0 ) = 0
| Исток вихревого поля всегда отсутствует |
| rot grad j | Ñ´(Ñj) = 0 | Векторное поле, имеющее градиент скалярной функции, всегда безвихревое, т.е. потенциальное |
rot div 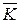
| Ñ´(Ñ 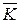 ) = 0 ) = 0
| Векторное поле, имеющее дивергенцию векторной функции, всегда безвихревое |
rot rot 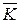
| Ñ´(Ñ´ 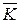 ) )
| 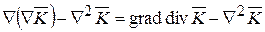
|
rot j 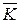
| Ñ´(j 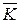 ) )
| 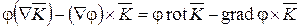
|
Теорема Остроградского-Гауса устанавливает соотношение между интегралом дивергенции вектора 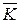 по объему V и поверхностным интегралом, взятым по замкнутой поверхности s, ограничивающей этот объем
по объему V и поверхностным интегралом, взятым по замкнутой поверхности s, ограничивающей этот объем
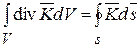 . (14.20)
. (14.20)
При этом поверхность должна быть кусочно-гладкой, а вектор на этой поверхности – непрерывным. Положительной является внешняя нормаль.
Теорема Стокса приравнивает поверхностный интеграл ротора вектора 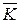 к линейному интегралу этого вектора, взятого по замкнутому контуру l, ограничивающему эту поверхность
к линейному интегралу этого вектора, взятого по замкнутому контуру l, ограничивающему эту поверхность
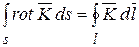 . (14.21)
. (14.21)
Вектор 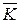 должен быть непрерывным по всему контуру интегрирования, а контур – кусочно-гладким.
должен быть непрерывным по всему контуру интегрирования, а контур – кусочно-гладким.
Date: 2015-07-24; view: 256; Нарушение авторских прав