Передача сигналов с дельта модуляцией

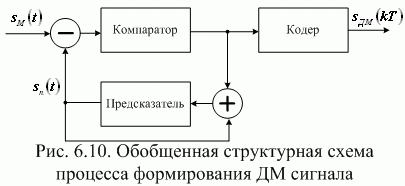
Дельта-модуляция (ДМ) – особый вид импульсной модуляции, при которой так же, как и при ИКМ, аналоговый сигнал 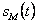представляется в виде дискретных отсчетов времени, квантованных по амплитуде. ДМ основана на существовании зависимости между отсчетами в речевом сигнале. При ДМ используется только один разряд для квантования разности соседних отсчетов. В этот разряд записывается полярность разности [5, 18, 20, 21, 32]. Важным элементом схемы (рис.6.10) при ДМ является компаратор, который разность 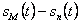входного сигнала 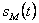и предсказанного 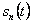, имеющего ступенчатый вид, квантует на два уровня. На выходе компаратора появляется значение 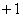если входной сигнал больше предсказанного (разность положительна); и 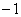если он меньше предсказанного сигнала (разность отрицательна).

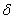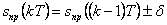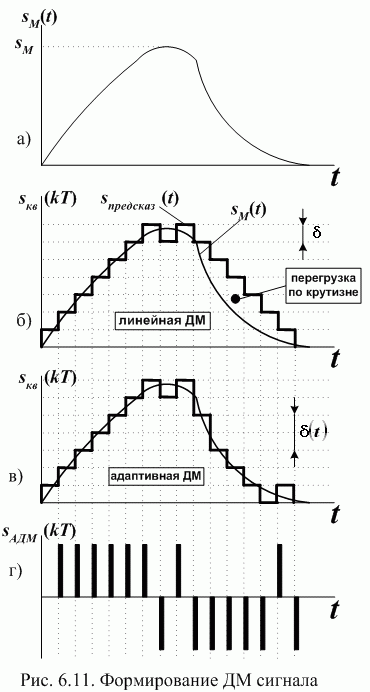
Закон возрастания (уменьшения) величины шага для предсказания выбирается исходя из статистических характеристик передаваемых сообщений. В частности, величина 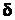может возрастать по линейному закону, по закону геометрической прогрессии, по экспоненциальному закону и другим законам, обеспечивающим требуемую точность передачи информации. При использовании постоянного шага (рис.6.11,б), необходимо иметь высокую тактовую частоту с целью предотвращения перегрузок по крутизне. Наиболее широко применяются методы адаптивной ДМ, один из которых иллюстрируется на рис. 6.11,в. При таком методе шаг предсказания 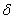меняется автоматически в соответствии с законом изменения крутизны (производной) сигнала 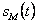. На рис. 6.11,в показано, что участку сигнала с большой крутизной соответствуют большие шаги квантования, что позволяет устранить искажения.

При создании цифровых систем связи применение ДМ является перспективным благодаря следующим особенностям:

устройства кодирования и декодирования ДМ сигналов характеризуются более простыми, чем при ИКМ, схемными решениями, что важно с точки зрения их надежности и стоимости;

ДМ сигналы по сравнению с ИКМ имеют большую устойчивость к сбою символов в каналах связи, поскольку «вес» каждого символа ограничен лишь значениями 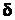. Вследствие этого пороговые свойства систем связи с ДМ несколько лучше, чем при ИКМ;

в системах связи с ДМ предъявляются менее жесткие требования к работе системы синхронизации.

Заключение

Сигналы с угловой модуляцией имеют ряд преимуществ перед амплитудно-модулированными.

Постоянство амплитуды ЧМ и ФМ сигналов позволяет обеспечить большую среднюю мощность излучения и коэффициент полезного действия передатчиков по сравнению с АМ. Увеличение помехоустойчивости при ЧМ и ФМ связано с необходимостью расширения спектра передаваемого сигнала. Поэтому угловая модуляция не используется в коротковолновом диапазоне.

Основным недостатком ФМ при практической реализации является необходимость учета многозначности фазы принимаемого сигнала при индексах модуляции m_ФМ > p, поэтому ЧМ нашла более широко применение в технике связи.

Благодаря открытию В.А. Котельниковым теоремы отсчетов стало возможным преобразовывать непрерывные аналоговые сигналы в импульсно-кодовые и цифровые сигналы.

Кроме того, используя результаты теоремы Котельникова, перешли от использования ЧРК к ВРК, которое дает возможность передачи информации с большим значением помехоустойчивости и меньшей вероятностью ошибки регенерации сигналов.

, т.е. .

Период следования прямоугольных импульсов определяется по теореме Котельникова .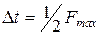

Теоретической основой получения цифрового сигнала из непрерывного является теорема Котельникова.

Первичный электрический сигнал чаще всего представляет собой непрерывную функцию от времени. Однако, во многих случаях целесообразно (или необходимо) преобразовать её в дискретный сигнал.

Данное преобразование получают путем замены функции f (t) последовательностью её отсчетов f (t_к), взятых через некоторый интервал времени Dt так, что t_к=k×Dt, где k = 1, N – целые числа.

При такой дискретизации сигналов появляется возможность одновременной передачи нескольких сообщений по одному каналу путем временного уплотнения каналов. То есть в промежутках между отсчетами одного сигнала передачи отсчетов других сигналов. При дискретизации сигналов появляются новые способы борьбы с помехами. Дискретный сигнал поддается кодированию, что облегчает задачу введения информации в ЭВМ и обмена данными между ними.

Дискретизация сигналов во времени должна осуществляться с минимальной потерей информации. Это значит, что дискретные отсчеты непрерывной функции времени должны быть достаточны для обратного преобразования их в такую же (или близкую) функцию времени на приемном конце.

Разработал

Доктор военных наук, профессор

А. Привалов

«» ____________ 2010 года

Date: 2015-07-24; view: 679; Нарушение авторских прав