Решение экспериментальных задач по физике в курсе механики

По большому счёту обучение ведётся для того, чтобы «научившийся» мог применять свои знания на практике. Поэтому важнейшим элементом обучения является практическое использование тех приборов и методов измерений, которые уже изучены школьниками.

Традиционно при изучении физики эксперименты разделяются на две большие группы: демонстрационные эксперименты, выполняемые обычно учителем, и практические (экспериментальные) работы, выполняемые школьниками самостоятельно.

Задача 1. Определить скорость вытекания воды из водопроводного крана.
Оборудование: стакан цилиндрической формы, штангенциркуль, секундомер.

Решение.
С помощью секундомера измеряем время  t наполнения стакана водой. Затем, используя штангенциркуль, найдем высоту стакана h и диаметр дна стакана d. Тогда объем стакана, а, следовательно, и воды равен V_в = (πd²/4)h.
Измерим диаметр сечения водопроводного крана  d_K и рассчитаем площадь сечения крана: S_K = πd_K²/4. (1) Определим скорость течения воды v_в = V_в/(S_Kt) Подставив значение S_K из уравнения (1), получим v_в = d²h/(d_K²t).

Задача 2. Исследовать зависимость скорости падения дробинок в глицерине от их радиуса.

Оборудование; измерительный цилиндр с глицерином, набор свинцовых дробинок различных размеров, линейка, секундомер, микрометр.

Решение.
При падении дробинок в глицерине (вязкой среде) сила сопротивления пропорциональна скорости их движения, следовательно, через некоторое время сила сопротивления будет равна силе тяжести дробинок, т. е. F_c = mg.
С этого момента дробинки будут падать равномерно и их скорость можно рассчитать, измеряя пройденное ими расстояние  l и время t: v = l/t.

Радиус дробинок r измерим микрометром.

Для исследования зависимости скорости падения дробинок от их радиуса необходимо построить график v = f(r).

Из графика видно, что зависимость между  v и r является квадратичной (v ~ r²). Поэтому можно построить график зависимости скорости от квадрата радиуса, т.е. v=φ(r²).

В этом случае графиком будет прямая линия. 

Задача 3. Определить массу груза.

Оборудование: динамометр, исследуемый груз, нить, масштабная линейка.

Решение.
Установим линейку  АВ так, чтобы момент силы тяжести, действующей на линейку, равнялся нулю. Для этого опора должна находиться на одной вертикали с центром тяжести линейки. В случае однородности материала линейки центр тяжести совпадает с ее геометрическим центром О. На расстоянии l от О расположим исследуемый груз, на расстоянии d укрепим динамометр и с его помощью установим линейку горизонтально (рис.).

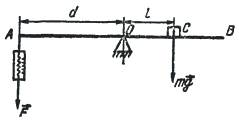
Тогда из условия равновесия получим следующее выражение:

Fd=mgl,(1)
Здесь F − сила, с которой динамометр действует на линейку, a m − масса исследуемого груза. Из выражения (1) получим:

m = Fd/(gl).

4. Определить массу шарика.

Оборудование: шарик неизвестной массы, прищепка для белья, спички, линейка, шарик известной массы.

Решение.
Спички будем использовать в качестве разновеса. Установим приблизительно массу одной спички. Для этого уравновесим одну прищепку на линейке некоторым количеством спичек. Масса прищепки  m_п будет равна

m_n =m_cn₁,
где m_с − масса спички, n₁ − число спичек, необходимое для того, чтобы уравновесить прищепку.

Зная  n₁ можем уравновесить шарик известной массы m, закрепленный прищепкой на линейке (иначе он будет скатываться), некоторым количеством спичек n₂. Считая, что масса каждой спички одинакова, находим ее. Во всех случаях плечо силы тяжести, действующей на уравновешиваемые предметы и спички, необходимо брать одинаковым, тогда

m_cn₂ =m_cn₁ +m_x,
отсюда

m_o =m/(n₂ −n₁).
Зная массу спички и прищепки, как и в предыдущем случае, уравновесим шарик неизвестной массы некоторым количеством спичек. Тогда, если число спичек  n₃, имеем:

m_cn₃ =m_cn₁ +m_x,
отсюда
m_x = (n₃ − n₁)m/(n₂ − n₁).

5. Определить массу шарика.

Оборудование: два стальных шарика (один из них известной массы), пластилин, штатив, транспортир, Две нити равной длины.  

Решение.
Прикрепим шарик известной массы  m₁ к нити длиной l, отведем его на измеряемый транспортиром угол α₁ (рис.) и отпустим.

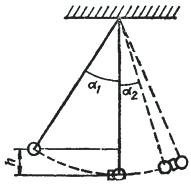
В нижней точке траектории движения шарика массой  m₁ подвесим шарик неизвестной массы m₂, к которому прикрепим кусочек пластилина массой Δm.
При своем движении шарик массой  m₁ сталкивается с шариком массой m₂. Из-за наличия пластилина удар шариков является неупругим, после столкновения они отклоняются на некоторый, тоже измеряемый угол α₂. При этом выполняется закон сохранения импульса:

m₁v₁ = (m₁ + m₂ + Δm)v₂.

Скорость  v₁ шарика известной массы в момент соударения находим из закона сохранения механической энергии
m₁gh = m₁v₁²/2, где h = l − lcosα₁ = l(1 − cosα₁)

v₁ =√{2gh}=√{2gl(1−cosα₁)}.
Поскольку масса кусочка пластилина  Δm ничтожна мала, в дальнейшем ею будем пренебрегать.

Аналогично определим скорость  v₂;

v₂ =√{2gl(1−cosα₂)}.
Тогда из закона сохранения импульса получим:

m₂ =m₁(√{(1−cosα₁)/(1−cosα₂)}−1).
И окончательно имеем:

m₂ = m₁(sin(α₁/2)/sin(α₂/2) − 1).

6. Определить массу линейки.

Оборудование: ученическая линейка, пятикопеечная монета или линейка и разновес.

Решение.

Первый способ.

Уравновесим систему, состоящую из линейки и пятикопеечной монеты, на какой-либо опоре (рис.). 

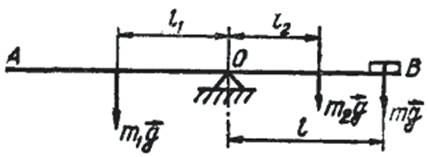
Условие равновесия этой системы (правило моментов) имеет вид:

m₁gl₁ = m₂gl₂ + mgl,

где m₁ − масса части линейки АО, m₂ − масса части линейки ОВ, m − масса пятикопеечной монеты (m = 5 г), l₁ − расстояние от точкиO до центра тяжести участка AO, l − расстояние от точки O до центра тяжести пятикопеечной монеты, l₂ − половина длины участка ОВ. Величины l₁, l₂, l легко измерить.
Обозначим через  ρ линейную плотность материала, из которого изготовлена линейка. Можем записать,
ρ = m_л/l_л = m₁/(2l₁) = m₂/(2l₂).

Мы учли, что центры тяжести участков  АО, ОВ линейки расположены посередине этих участков. При этом условие равновесия примет вид:
2ρl₁² = 2ρl₂² + ml.

Из последнего равенства находим, что ρ = ml/(2(l₁ + l₂)(l₁ − l₂)).
Поскольку m_л =ρl_л, где l_л =2(l₁ +l₂),
то окончательно

m_л =ml/(l₁ −l₂)
Второй способ.

Так как сила тяжести линейки приложена к ее середине (рис.), 

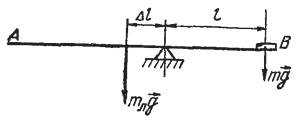
то условие равновесия системы линейка − монета (разновесок) имеет вид:

m_лgΔl = mgl,

откуда:
m_л = ml/Δl.

Нетрудно показать, что Δl = l₁ − l₂, где l₁ и l₂ указаны на рисунке. Очевидно, что второй способ решения более рационален.

7. Определить массу тела.

Оборудование: металлическая линейка, медная проволока малого диаметра, карандаш, тело неизвестной массы, штатив.

Решение.

Закрепим карандаш в штативе. Уравновесим линейку на карандаше, закрепим на одном из ее концов тело, массу которого надо определить. Надевая на второе плечо полученного рычага проволочную петлю и натягивая проволоку по вертикали вниз, уравновесим тело (рис.). 

Запишем условие равновесия рычага: 

mgl₂ = F_yh. (1)

Из выражения (1) видно, что чем меньше плечо  h, тем больше должна быть сила F_y. Очевидно, что уменьшая l₁ путем перемещения петли к опоре, мы можем достигнуть такого положения, при котором проволока оборвется.
В этом случае

F_y = σ_nS, (2)

где σ_n − предел прочности меди при растяжении (значение находим по справочнику), a S = πd²/4 площадь поперечного сечения проволоки. Подставив выражение (2) в (1), получим:

mgl₂ = σ_nl₁πd²/4 (3)

откуда

m = πd²l₁σ_n/(4l₂g). (4)

Диаметр проволоки d определим, намотав ее на карандаш и измерив общую толщину п витков. Пусть она равна L_o, тогда d = L_o/n.
Подставив значение диаметра проволоки в выражение (4), окончательно получим:

m = πl₁σ_nL_o2/(4l₂gn²).

8. Определить массу водяной капли.
Оборудование: ведро с водой, маленький сосуд с широким горлышком, несколько однокопеечных монет, пипетка, мягкий карандаш. Решение.
Погрузим сосуд в ведро с водой так, чтобы горлышко его было направлено вверх и находилось над водой. Теперь начнем наполнять сосуд монетами, пока он не будет плавать в вертикальном положении. Поместим в сосуд еще одну-две монеты, на наружной стороне его отметим карандашом уровень воды. Достанем из сосуда одну монету, при этом равновесие нарушится, и он чуть-чуть всплывет. Добавляя из пипетки по каплям в сосуд воду и считая число капель (пусть оно равно  n), добьемся, чтобы сосуд опустился до прежнего уровня. Нетрудно заметить (попробуйте обосновать это теоретически), что масса воды mв, добавляемой в сосуд, равна массе копейкиm_к = 1 г, Тогда масса одной капли будет равна

m = m_в/n = m_к/n.

9. Имеется 8 совершенно одинаковых по размеру и виду шаров, изготовленных из одного материала. В одном из шаров имеется полость. Найти шар с полостью, пользуясь весами, причем разрешается произвести только два взвешивания. Найти минимальное число взвешиваний, при которых будет определен полый шар, находящийся в группе с произвольным числом шаров.
 Оборудование: 8 шаров, весы.

Решение.
На чашки весов кладем по три шара. При этом возможны два случая. 
а) Чашки с шарами уравновешены и, следовательно, полый шар − среди оставшихся двух. Сняв с чашек ранее положенные шары, на каждую из них положим по шару из оставшейся пары. Перевесивший шар не является полым. 
б) Равновесие не установится и, следовательно, полый шар находится в тройке шаров, которая легче. Освободив чашки весов от трех шаров, кладем на каждую из них по шару из тройки, в которой полый шар. Если шары уравновесились, значит, оставшийся шар − полый. Если равновесие отсутствует, то полый шар тот, который легче. 
Задача может быть решена таким же образом в случае произвольного числа шаров, среди которых один полый. Минимальное число взвешиваний m, при которых наверняка будет определен полый шар, можно найти, рассуждая следующим образом. Максимальное число шаров, из которых можно всегда определить полый, произведя только одно взвешивание, равно  3 (это нетрудно проверить), два взвешивания − 32, три − 33, m взвешиваний − 3m = n. Логарифмируя последнее равенство по основанию 3, получим

m = log₃п,

где n − число шаров.

Примечание 1. Если m не целое число, его необходимо округлить до большего целого числа.

Примечание 2. Алгоритм для определения полого шара из одинаковых по размеру шаров таков: n шаров делим на три группы. Всегда (если эти группы не равны) Можно сделать две группы с равным числом шаров, тогда в третьей группе число шаров будет либо больше, либо меньше на один шар, чем в первых двух. Положив равные группы на чашки весов, в случае равновесия ищем полый шар среди оставшихся. Если же равновесия нет − ищем шар в более легкой группе. Опыт при этом повторяется. 

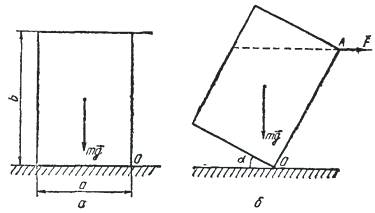
10. Определить силу, необходимую для того, чтобы опрокинуть брусок через точку O. Сила приложена в точке A параллельно верхнему основанию бруска (рис.).

Оборудование: деревянный брусок известной массы, линейка.

Решение.
Сила, приложенная в точке  A (рис. а) и необходимая для того, чтобы опрокинуть брусок вращением его вокруг ребра, перпендикулярного плоскости рисунка и проходящего через точку O, определяется из условия равенства моментов этой силы и силы тяжести относительно точки O. В начальный момент времени (рис. а) плечо силы F равно b, а плечо силы тяжести − a/2.

Учитывая это, равенство указанных моментов запишется в виде: 
mga/2 = Fb,

откуда

F = mga/(2b).

Покажите, что в случае поворота бруска на угол  α (рис. б) сила F, вращающая брусок, будет меньше по сравнению с начальным значением (рис. а).

11. Определить давление, производимое стальной иглой при прокалывании медной пластины.
Оборудование подобрать самим.

Решение.
Силу давления можно определить с помощью динамометра, а сечение острия головки рассчитать, используя измеренный штангенциркулем диаметр. Тогда давление на медную пластинку, созданное острием иглы, 

p = 4F/(πd²),

где F − показания динамометра, d − диаметр острия иглы.
Подумайте, можно ли измерить диаметр острия иглы, используя микроскоп. 

12. Определить прочность нити.

Оборудование: грузы из набора по механике, транспортир, штатив, нить, гирька известной массы.

Решение.
Привяжем к нити гирьку и прикрепим ее второй конец к штативу, отведем гирьку от положения равновесия на небольшой угол и отпустим. Меняя угол и массу гирьки найдем то значение угла, при котором нить обрывается в момент прохождения положения равновесия. Пусть этот угол равен  φ₀, а масса гири равна m. Рассмотрим силы, действующие на гирю в положении равновесия.
Ими будут сила тяжести mg и сила реакции нити F_p (рис.).

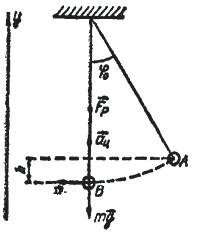
Запишем второй закон Ньютона для нити 
F_p + mg = mа_ц, (в векторном виде)

где а_ц − центростремительное ускорение.
Проекция на ось ординат дает

F_p − mg = mа_ц,

отсюда
F_p = mg + mа_ц. (1)

Прочность нити как раз и определяется силой  F_p, т. е. она является искомой величиной в выражении (1).
Так как a_ц =v²/l,
где l − длина нити, то
F_p = m(g + v²/l). (2)

Для нахождения v²/l используем закон сохранения механической энергии (для точек A и B). В этих точках энергии имеют значения:

Е_pА = mgh; Е_кA = 0; Е_рB = 0; Е_кВ = mv²/2.

Используя закон сохранения энергии, получим:
mgh=mv²/2.
Из геометрических соображений

h=l−lcosφ₀,
тогда

gl(1 − cosφ₀) = v²/2, v²/l = 2g(1 − cosφ_о).

Подставив полученное значение в (2), получим:

F_p = mg(3 − 2cosφ_o).

13. Определить жесткость резинового шнура.
Оборудование: два штатива с лапками, резиновый шнур, грузы известной массы, линейка.

Решение.
Закрепим шнур, имеющий длину  l₀, между двумя штативами и подвесим к его середине груз массой m. Условие равновесия для указанной системы (рис.)

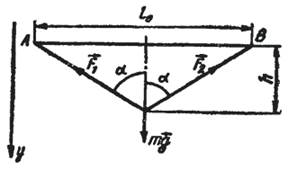
в проекции на вертикальное направление (ось y) запишется в виде:

mg − F₁cosα − F₂cosα = 0. (1)

Исходя из условия симметрии имеем:

F₁ − F₂ = F.

Тогда формула (1) запишется в виде:

mg − 2Fcosα = 0.

Учитывая, что
F = kx,

где x = l/2 − l_o/2, длина шнура после растяжения его грузиком, а cosα = 2h/g, получим:
mg − (2k(l − l_o)/2)•(2h/l) = 0.

Отсюда
k = mgl/(2(l − l_o)h).

Величины l, l₀, h измеряются линейкой.

Опыты необходимо проделать с различными грузиками.

14. Определить приближенное значение коэффициента трения песка о стекло.
Оборудование: песочные часы, линейка.

Решение.
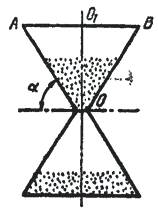Чтобы песочные часы оправдывали свое назначение, песок в них должен течь равномерно. Из рисунка видно, что песчинки будут двигаться равномерно, если сумма сил, действующих на них, будет равна нулю. 
Тело, находящееся на наклонной плоскости, будет двигаться равномерно при условии, что 

tgα = μ,

где μ − коэффициент трения.
Таким образом, наша задача сводится к определению  tgα.
Нетрудно видеть (рис.), что
tgα = |OO₁|/|AO₁|;

|AO₁| = (1/2)|AB|, |OO₁| = (1/2)√{4|AO|² − |AB|²},

тогда
tgα = √{4|AO|² − |AB|²}/|AB|.

Теперь осталось измерить величину  |AO| и |AB|, что легко сделать с помощью линейки.

15. Определить коэффициент трения бруска о горизонтальный стол, если длина и ширина бруска меньше его высоты.
Оборудование: брусок, нить, линейка.  

Решение.
Для того чтобы брусок сдвинуть с места, необходимо у его основания  ABCD (места приложения сил трения) подействовать силой F. Запишем условие равномерного движения бруска по поверхности стола:

F = F_mp. (1)

Если силу F переносить параллельно вверх от основания АВСD (рис.),

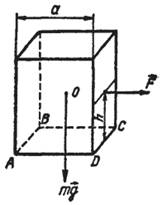
то равномерное и прямолинейное движение бруска будет продолжаться, а брусок не будет поворачиваться относительно ребра основания DC до тех пор, пока вращающий момент силы не превысит момент силы тяжести mg относительно DC. Тогда из условия

Fh=mga/2 (2)
находим, что

F=mga/(2h),(3)
где h − плечо силы F, при котором брусок начинает переворачиваться.
Коэффициент трения
μ=F_mp/(mg).
Из уравнений (1) и (3) находим, что 

μ = a/(2h).

16. Исследовать зависимость КПД наклонной плоскости от угла ее наклона к горизонту.
Оборудование: трибометр, брусок, линейка ученическая, секундомер. Решение.
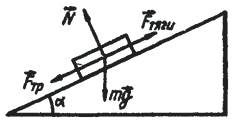Как известно, КПД наклонной плоскости (рис.)

η = (A_n/A_c)•100 %,

где А_n = F_тяг/l − полезная работа, т. е. работа по равномерному подъему тела без трения (l − длина наклонной плоскости), а А_с = F_тягl − работа при наличии трения (совершенная работа).
Запишем второй закон Ньютона для равномерного движения 
F_тяг +F_mp +N+mg=0 (в векторном виде).

В проекции на оси координат после несложных преобразований получим:

F_тяг =mg(sinα+μcosα).
Если трение отсутствует, то μ = 0 и тогда

F_тяг^/ =mgsinα.
Таким образом,

η=sinα/(sinα+μcosα),
или

η=1/(1+μctgα).
Отсюда следует, что для того, чтобы найти η как функцию угла α, надо знать коэффициент трения μ. Для определения μ подберем угол наклона α₀ трибометра (наклонной плоскости) таким образом, чтобы брусок двигался сниз с небольшим (подумайте почему) ускорением. Тогда

l=at²/2.(1)
Длину наклонной плоскости  l измеряем линейкой. Время движения определим по секундомеру.

Из выражения (1) имеем:
а=2l/t².(2)
Из второго закона Ньютона имеем:

ma=mgsinα₀ −μmgcosα₀.(3)
Совместное решение уравнений (2) и (3) дает:

μ = (gsinα_o − 2l/t²)/(gcosα_o). (4)

Преобразовав выражение (4), имеем:

μ=tgα_o −2l/(gt²cosα_o).
Измерив КПД наклонной плоскости при различных углах наклона, следует отметить полученные значения КПД на графике  η = f(α).

17. Стреляя из баллистического пистолета, установленного на столе, попадите, произведя только два выстрела, в картонную коробку, стоящую на полу (на столе).
Оборудование: баллистический пистолет, рулетка, коробка.
Примечание. Вначале разрешается произвести любое число выстрелов. Затем устанавливается коробка и разрешается произвести только два выстрела. Решение.
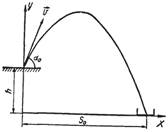Установим баллистический пистолет под углом αо к плоскости стола и произведем выстрел из него (рис.). По известному расстоянию и высоте стола находим начальную скорость «снаряда», вылетающего из пистолета. 
Запишем уравнения изменения координат снаряда со временем (уравнение движения): 

y = h + v_oyt − gt²/2, (1)

x=v_oxt,(2)
где

v_oy =v_osinα_о
и

v_ox =v_ocosα₀.
Подставив значения v_ox и v_oy в выражение (1) и (2), имеем:

y = h + v_osinα₀ − gt²/2, (3)

х=v_ocosα_ot.(4)
Выразив из уравнения (4) время t и подставив его значение в выражение (3) с учетом того, что в момент падения x = S_o, y = 0, получим:

h+s_otgα_o −(g/2)(s_o²/(v_o²cos²α_o)).(5)
После несложных преобразований находим, что

v_o =(s_o/cosα_o)√{g/(2(h+s_otgα_o))}.
Зная значение v_o и измерив расстояние s от стола до коробки (по горизонтали), мы можем рассчитать значение угла α, под которым надо установить пистолет, чтобы попасть в коробку. Для этого в выражение (5) вместе s_o и α_o подставим s и α, после чего оно примет вид:

h+stgα−gs²/(2v_o²cos²α)=0.(6)
Рассматривая выражение (6) как тригонометрическое уравнение для определения α и решив его, находим, что

α = (1/2)(arcos[(gs² − v_o²h)/(v_o²√{h² + s²})] + arcos[h/√{h² + s²}]).
Установив пистолет под рассчитанным углом  α, произведем выстрел в коробку.
Возможно также проведение серии выстрелов вертикально вверх или горизонтально с целью нахождения средней скорости вылета снаряда и пределов отклонения скорости от этого среднего значения. По пределам отклонения скоростей можно оценить область попадания. Если размеры коробки больше размеров области попадания, производят  2 выстрела. Второй выстрел предлагается для избежания случайного резкого отклонения скорости снаряда от средней величины.

18. На каком максимальном расстоянии от центра диска электропроигрывателя может удержаться монета при вращении с заданной угловой скоростью?
Оборудование: проигрыватель, медная монета.

Решение.
Так как монета вращается, то на нее действует центростремительная сила 

F_ц = ma_ц = 4π²Rmv², (1)

где m − масса монеты, R − расстояние от центра диска до центра монеты, ν − частота вращения диска. В данном случае центростремительной силой будет являться сила трения

F_mp = μmg, (2)

где g − ускорение свободного падения, μ − коэффициент трения. Приравняем выражения (1) и (2):

μmg = 4π²Rmv²,

откуда:

R = μg/(4π²ν²).

Коэффициент трения  ν = tgα_o находим из предварительных опытов по определению предельного угла α_o наклона диска, при котором монета начинает скользить по диску. В этом случае, как известно,

μ = tgα_o.

Окончательно получаем, что монета может удержаться на расстоянии
R = gtgα_o/(4π²ν²).

19. Придумать способ определения потенциальной энергии растянутого резинового шнура.

Решение.
Потенциальная энергия резинового шнура  Е_p равна

E_p = k(Δl)²/2. (1)

Чтобы найти жесткость шнура, необходимо к нему подвесить груз известной массы  m. Условие равновесия запишется следующим образом:

kΔl_o = mg,

где Δl_o − величина удлинения резинового шнура при подвесе к ней массы m.
Отсюда:

k = mg/Δl_o.

Подставив значение k в формулу (1), будем иметь:

E_p = mg(Δl)²/(2Δl_o),

где Δl_o, Δl − величины, измеряемые линейкой.
Таким образом, для определения потенциальной энергии растянутой резинки указанным способом необходимо иметь груз известной массы и линейку. Возможны и другие способы решения. 

20. Определить максимальную скорость движения пальца руки.
Оборудование: камешек, линейка.

Решение.
Положив камешек на край стола, щелкнем по нему пальцем и заметим точку падения камешка на пол. Измерим максимальное расстояние  l от стола до места падения камешка, полученное в результате нескольких опытов. Тогда максимальная скорость пальца v(скорость, сообщенная в данном опыте камешку) вычислим по формуле:

v = l/t, (1)

где t (время полета камешка) можно определить по формуле

t = √{2h/g}. (2)

Здесь h − высота стола, а g − ускорение свободного падения.
Подставляя t из формулы (2) в формулу (1), получим:

v = l/√{2h/g}.

Предложите другие возможные способы определения максимальной скорости пальца руки. 

Заключение

Устаревшая материальная база многих кабинетов физики и другие субъективные причины приводят к тому, что преподавание физики становится «меловым». Учителя пытаются вернуть эксперимент на уроки физики в виде фронтального эксперимента с использованием простейшего оборудования («простой физический опыт») или в виде экспериментальных задач, которые могут быть поставлены как фронтально, так и демонстрационно. Практически любой занимательный опыт или программная демонстрация могут быть трансформированы в экспериментальную задачу. Ценность такой задачи в том, что сразу после разных ответов разных учащихся можно получить правильный ответ.

При обучении школьников решению качественных экспериментальных задач следует договориться о «правилах игры». Это необходимо потому, что ученик часто отвечает не на вопрос учителя, а на «свой вопрос», связанный с той частью опыта, которая произвела на него самое большое впечатление. (Можно вспомнить, замечают ли учащиеся образование тумана в толстостенном сосуде, из которой с шумом вылетела пробка?) Чтобы избежать таких досадных недоразумений, нужно договориться, что каждый ответ будет начинаться со слова «Наблюдаю» и описания увиденного. Когда описание увиденного окончено, надо произнести другое ключевое слово: «Объясняю». Закончить ответ нужно словами «Делаю вывод» и формулировка вывода.

Часто при проведении опыта учителя описывают свои действия. Как правило, это описание излишне подробное, дети сами видят, что вы берете в руки. Также многословие учителя при показе опытов отвлекает учащихся от наблюдений, рассеивает их внимание, утомляет. Поэтому многие учащиеся просто не слышат вопроса, который следует после монолога учителя.

Чтобы активизировать внимание учащихся, можно предложить и такой прием. Если для проведения опыта нужна специальная установка и она заранее собирается учителем, тогда учащиеся называют ее основные части. Только после этого формулируется вопрос, ответ на который должны дать учащиеся.

Итак, любой занимательный опыт или программная демонстрация могут быть трансформированы в экспериментальную задачу. Наиболее эффективный способ обучения – это ученический физический эксперимент.

Список литературы

1. Акритов X. Развитие интереса учащихся к механике // Физика в шко-ле. 1985.№4,с.38-44.

2. Александров Д.А., Швайченко И.М. Методика решения задач по физике всредней школе: Пособие для учителей,- Л.:Учпедгиз, 1948.-240 с.

3. Антипин И.Г. Экспериментальные задачи по физике в 6-7 классах: Пособиедля учителей. М.Просвещение, 1974. - 127 с.

4. Балашов М.М. Физика: Учебник для IX класса общеобразовательных учреждений. М.: Просвещение, 1994. - 319 с.

5. Беликов Б.С. Решение задач по физике. Общие методы: Учебное пособие длястудентов вузов. М.: Высшая школа, 1986. - 256 с.

6. Берлеев Г.И. Сборник задач и вопрос по физике. М.: Учпедгиз, 1955. - 125 с.

7. Блохин B.C. Особенности познавательной деятельности учащихся при решении творческих задач // Психологические основы рационализации познавательно-практической деятельности учащихся. Ярославль, 1975. -с.34-40.

8. Бугаев А.И. Методика преподавания физики в средней школе: Теоретические основы. М.: Просвещение, 1981. - 288 с.

9. Буров В.А., Иванов А.И., Свиридов В.И. Фронтальные экспериментальные задания по физике. М.: Просвещение, 1985, - 62 с.

10. Буров В.А. и др. Фронтальные экспериментальные задания по физике в 6-7классах средней школы: Пособие для учителей / В.А.Буров, С.Ф.Кабанов, В.И.Свиридов.- М.: Просвещение, 1981. 112 с.

11. Бутырский Г.А. Проблема использования экспериментальных задач при обучении физике в старших классах средней школы: Диссертация. кандидата педагогических наук в виде научного доклада. Киров, 1995. - 26 с.

12. Володарский В. Система задач как средство повышения эффективности обучения физике в средней школе: Диссертация. кандидата педагогических наук.-М., 1979.-239 с.

13. Голубовская М.П. Современный подход к решению задач по механике в курсе физики средней школы: Диссертация. кандидата педагогических наук. Санкт-Петербург, 1992. - 166 с.f* 32. Горев JI.A. Занимательные опыты по физике. М.: Просвещение, 1977. - 151с.

14. Грязева Н. Н. Творческие задачи по физике как средство формирования познавательной деятельности учащихся. Диссертация. кандидата педагогических наук. - Челябинск, 1996. - 170 с.

15. Давиден А.А. Экспериментальные задачи как средство повышения уровня и качества знаний учащихся по физике: Диссертация. кандидата педагогических наук. М., 1990. - 184 с.

16. Демкович В.П. Сборник вопросов и задач по физике. М.: Просвещение,1970.-240 с.

17. Довнар Э.А., Курочкин Ю.А., Сидорович П.Н. Экспериментальные олимпиадные задачи по физике. Минск: Народная асвета, 1981. - 96 с.

18. Евсеева Н.М. Экспериментальные упражнения в курсе физики как средство организации познавательной деятельности учащихся подросткового возраста: Диссертация. кандидата педагогических наук. М., 1990. - 189 с.

19. Знаменский П.А. Методика преподавания физики. 2-е изд. - М.: Учпедгиз,1954.-551 с.

20. Искандеров Н.Ф. Экспериментальные задачи как средство формированиязнаний о физическом явлении и развитии логического мышления в курсе физики основной школы: Диссертация. кандидата педагогических наук. -Челябинск, 1993. 195 с.

21. Мошков С.С. Постановка экспериментальных задач на уроках физики всредней школе: Диссертация. кандидата педагогических наук. Ленинград, 1953. - 242 с.

22. Мошков С.С. Экспериментальные задачи по физике в средней школе.

23. вопросы в курсе физики средней школы. М.: Просвещение, 1979. - 85 с.

24. Тулькибаева Н.Н., Фридман Л.М., Драпкин М.А., Валович Е.С., Бухарова,. Решение задач по физике: Психолого-методический аспект. Челябинск, 1995. - 119 с.

25. Тульчинский М.Е. Качественные задачи по физике: Пособие для учителя.: Просвещение, 1972. 239 с.

26. Хомутский В.Д. Познавательные задачи по физике. Челябинск: Изд-во1. ЧГПИ,1990. 150 с.

27. Шунин И.А. Совершенствование содержания и методики решения экспериментальных задач по физике в условиях современной школы: Диссертация. кандидата педагогических наук. Самара, 1995. - 197 с.

28. Эвенчик Э.Е. Преподавание механики в курсе физики средней школы. М.:1. Просвещение, 1967. 179 с.