Тема №6. Усилия на лопатках и работа вращения колеса ступени. теорема Эйлера

Вывод уравнений для расчета усилий, действующих на лопатку, проведем для ступени осевого турбокомпрессора, а затем преобразуем полученные результаты применительно к турбинной ступени.

Выделим малый по высоте участок степени 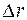. Этот участок принято называть элементарной ступенью.

Изобразим развертку РК элементарной ступени (рис. 6.1).

При известных параметрах потока силы, действующие на лопатки, и работа, затрачиваемая на его вращение, могут быть определены с помощью теоремы Эйлера в предположении установившегося движения.

Выделим в потоке объем, ограниченный контрольной плоскостью, состоящей из поверхностей тока 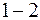и 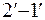, отстоящих друг от друга на величину шага решетки 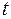, и двух поверхносте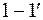й и 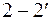, параллельных фронту решетки и расположенных на таком расстоянии, чтобы было можно пренебречь неравномерностью потока.

Обозначим 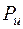и - окружную и осевую составляющие аэродинамической силы 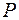, действующей на лопатку. Сила 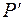, с которой лопатка воздействует на поток, равна по величине и противоположна по направлению силе .

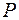Согласно теореме Эйлера, сумма всех сил, действующих на выделенный объем воздуха, равна разности количеств движения потоков, вытекающих и втекающих этот объем в единицу времени.

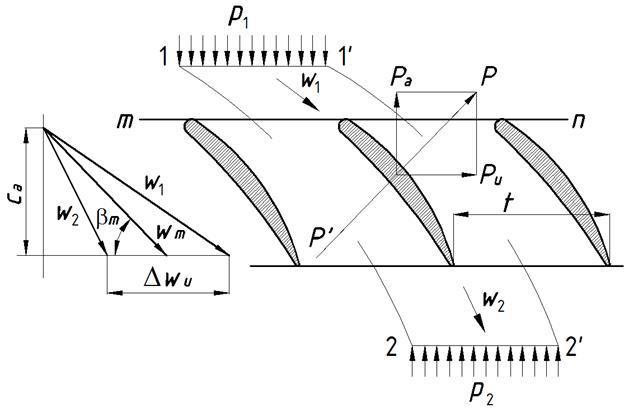
Рис. 6.1. К определению усилий на лопатках рабочего колеса

Из рассмотрения рис. 6.1 понятно, что силы, действующие на поверхностях 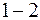и 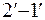, компенсируют друг друга, а расход через них равен нулю.

Исходя из этого, кроме силы 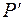, учету будут подлежать только количества движения и силы давления в сечениях 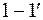и .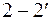

Рассматривая проекции этих сил в окружном и осевом направлениях, можно получить:

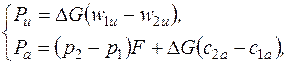(6.1)

где 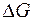- массовый расход через выделенный объем, .

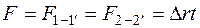Согласно уравнению неразрывности:

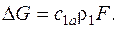(6.2)

Если число лопаток колеса равн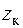о , то

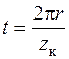. (6.3)

Тогда силы, действующие на единицу длины лопатки, будут равны:

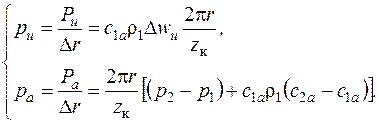(6.4)

Эти соотношения используются при расчетах лопаток компрессоров на прочность.

В предположении, что 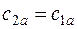(идеальная несжимаемая жидкость) для относительного движения, из уравнения Бернулли (1.12) можно получить:

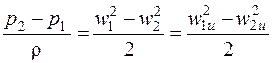(6.5)

или

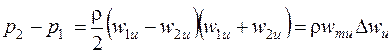. (6.6)

Кроме того, из (6.4), с учетом (6.5) и (6.6), можно легко получить:

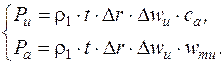(6.7)

Зная проекции силы, можно найти и ее суммарную величину:

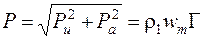, (6.8)

где величина 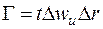- циркуляция скорости вокруг одного профиля в решетке.

Отношение же составляющей этой силы:

(6.9)

получило название теоремы Жуковского о подъемной силе крыла.

Из теоремы Жуковского следует, что теоретически подъемная сила будет увеличиваться с ростом угла поворота потока в решетке.

Однако в реальности, как мы уже говорили, большой угол поворота потока приведет к его срыву с профиля.

Определим работу , затрачиваемую на вращение элементарной ступени, в расчете на 1 кг/с массового расхода.

Если окружная скорость рабочего колеса 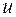, то секундная работа вращения лопатки будет равна 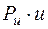, что ясно из физики.

Тогда

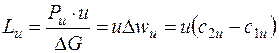. (6.10)

Таким образом, работа вращения колеса пропорциональна окружной скорости и закрутке воздуха в колесе.

При условии, что :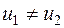

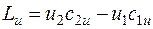(6.11)

или

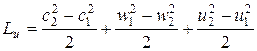. (6.12)

При переходе от ступени осевого компрессора к турбинной ступени по причине других кинематических соотношений формулы примут несколько иной вид.

Мощность, развиваемая потоком рабочего тела на рабочих лопатках ступени, может быть найдена по формуле:

,

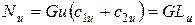где 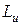-- удельная работа ступени, т.е. мощность, приходящаяся на каждые 1 кг/с массового расхода.

Можно также показать, что

.

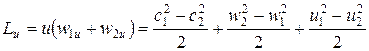Date: 2015-07-24; view: 1197; Нарушение авторских прав