
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчеты мгновенных схем в тяговых сетях переменного тока
|
|
Модуль 2. Принципы построения методов расчета системы электроснабжения. Выбор параметров системы электроснабжения
Лекция №9, 10. Расчеты мгновенных схем для участков переменного тока (2 часа)
План лекции:
1. Расчеты мгновенных схем в тяговых сетях переменного тока.
Расчеты мгновенных схем для участков переменного тока.
Расчеты мгновенных схем в тяговых сетях переменного тока
Линии с односторонним питанием. Однопутные участки и многопутные при параллельном питании приводов смежных путей (см. рис. 5.1). Для расчета токов фидеров и плеч питания применяют аналогичную формулу (5.1) для постоянного тока. В общем случае в фидерной зоне или на плече питания расположены нагрузки о различными углами сдвига фаз. Поэтому ток фидера или плеча подстанции здесь равен геометрической сумме токов нагрузок. В комплексной форме (для синусоидальных нагрузок)
 . (5.1)
. (5.1)
Значении входящих сюда букв те же, что и в формуле (5.1). Индуктивные нагрузки можно представить в виду 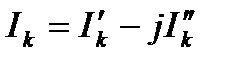 . Отсюда
. Отсюда
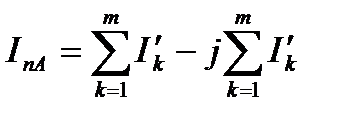 . (5.2)
. (5.2)
Таким образом, полный ток фидера (плеча подстанции) также может быть выражен через активную и реактивную составляющие: 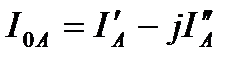 .
.
Необходимо заметить, что все активные и реактивные составляющие токов при заданном угле сдвига фаз определяются относительно «своего» напряжения на токоприемнике, а так как напряжения эти сами сдвинуты друг относительно друга по фазе вследствие падший напряжения в сети между поездами, то и активные и реактивные составляющие отдельных поездов тоже не совпадают по фазе. Однако этот сдвиг по фазе весьма невелик, и им в расчетахпренебрегают, т. е. принимают, что все активные составляющие нагрузок и все реактивные совпадают по фазе так, как это записано в уравнении (5.2).
В гл. 2 было отмечено, что для расчетов существенно важным является не падение напряжения, а потеря его, определяющая напряжение у потребителя, и было дано выражение для ее определения при одной
 . (5.3)
. (5.3)
В формуле (5.3) выражение 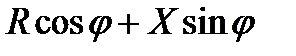 измеряется в омах и называется составным сопротивлением. Эта формула может быть представлена в ином, более удобном виде, если заменить
измеряется в омах и называется составным сопротивлением. Эта формула может быть представлена в ином, более удобном виде, если заменить 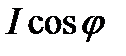 на
на 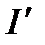 и
и 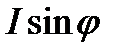 на
на 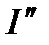 , т. Е. через активную и реактивную составляющие тока. Тогда
, т. Е. через активную и реактивную составляющие тока. Тогда
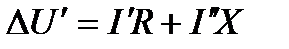 . (5.4)
. (5.4)
Как видно, потеря напряжения равна алгебраической сумме потерь напряжения от активной составляющей тока в активном сопротивлении и от реактивной составляющей в реактивном сопротивлении.
Наконец, можно выразить активную и реактивную составляющие тока через соответствующие составляющие мощности 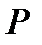 и
и 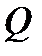 . При этом, очевидно,
. При этом, очевидно,
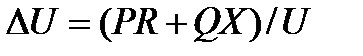 , (5.5)
, (5.5)
где 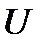 — расчетное напряжение у электровоза, при котором определены активная и реактивная мощности. В расчетах его принимают равным номинальному.
— расчетное напряжение у электровоза, при котором определены активная и реактивная мощности. В расчетах его принимают равным номинальному.
Практически сопротивления сети 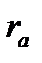 и
и 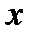 , отнесенные к 1 км, как это и было принято выше (см. гл. 2), считают постоянными по длине т. е.
, отнесенные к 1 км, как это и было принято выше (см. гл. 2), считают постоянными по длине т. е. 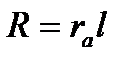 и
и 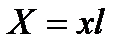 .Тогда:
.Тогда:
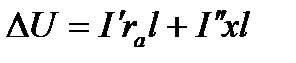 ; (5.6)
; (5.6)
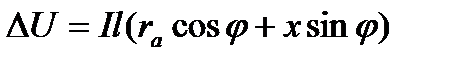 ; (5.7)
; (5.7)
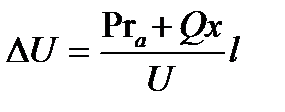 . (5.8)
. (5.8)
Рис. 5.1. Линия однофазного тока с двумя нагрузками:
а – схема линии; б – векторная диаграмма; в – упрощенная векторная диаграмма
Если в фидерной зоне (или на плече подстанции) расположен ряд нагрузок с различными 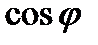 (рис. 5.1, а), векторная диаграмма имеет вид, показанный на рис. 5.1, б (для упрощения рассмотрен только случай с двумя нагрузками). При построении векторной диаграммы откладывают вектор
(рис. 5.1, а), векторная диаграмма имеет вид, показанный на рис. 5.1, б (для упрощения рассмотрен только случай с двумя нагрузками). При построении векторной диаграммы откладывают вектор 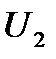 (напряжение в конце линии у нагрузки
(напряжение в конце линии у нагрузки  ) в под углом
) в под углом 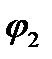 , к нему — вектор
, к нему — вектор 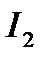 . Для получения напряжения
. Для получения напряжения 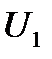 (у нагрузки
(у нагрузки 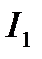 ) к
) к 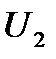 геометрически добавляются активная и реактивная составляющие падения напряжения в сети на расстоянии между первой и второй нагрузками (сопротивления
геометрически добавляются активная и реактивная составляющие падения напряжения в сети на расстоянии между первой и второй нагрузками (сопротивления 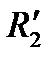 и
и 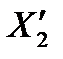 ). Имея вектор
). Имея вектор 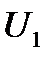 ,можно отложить вектор
,можно отложить вектор 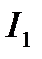 под углом
под углом 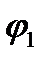 к
к 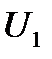 .
.
Сложив затем (геометрически) 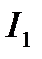 и
и 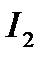 , получим ток
, получим ток 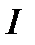 на участке
на участке 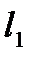 . Геометрическая сумма
. Геометрическая сумма  ,
, 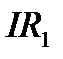 , и
, и 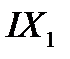 дает напряжение на шинах подстанции —
дает напряжение на шинах подстанции — 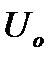 .
.
При расчетах, как это уже было отмечено применительно к формуле (5.1), обычно пренебрегают углом 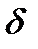 между
между 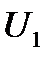 и
и 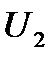 из-за его малости в откладывают углы
из-за его малости в откладывают углы 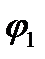 ,
, 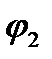 от вектора
от вектора 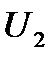 (pис. 5.1, в). В этом случае потеря напряжения до некоторой нагрузки в номером
(pис. 5.1, в). В этом случае потеря напряжения до некоторой нагрузки в номером 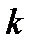 по аналогииcтаким же случаем при постоянном токе (см. п. 5.2) определится формулами:
по аналогииcтаким же случаем при постоянном токе (см. п. 5.2) определится формулами:
 ; (5.9)
; (5.9)
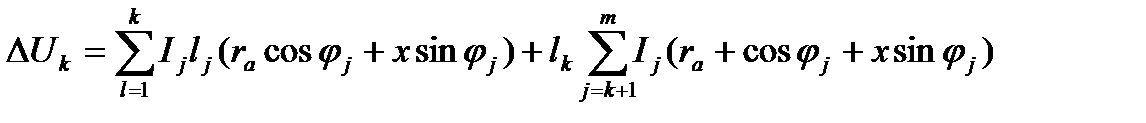 . (5.10)
. (5.10)
В частности, при равных углах сдвига фаз
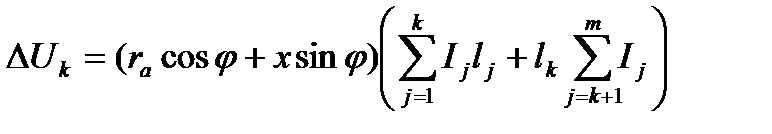 , (5.11)
, (5.11)
т. е. задача решается как для постоянного тока о заменой лишь сопротивления сети постоянному току составным сопротивлением в соответствии с формулой:
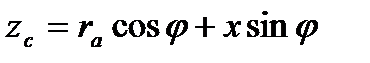 . (5.12)
. (5.12)
В гл. 2 отмечалось, что для участков однофазного тока с выпрямительными электровозами токи в тяговой сети несинусоидальны. Однако расчеты потерь напряжения в этом случае можно вести так же, как для синусоидальных токов, с топ лишь разницей, что вместо составного сопротивления  берется согласно формуле эквивалентное сопротивление
берется согласно формуле эквивалентное сопротивление 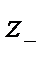 , приведенное к выпрямленному напряжению, а вместо действующих значений токов — выпрямленные токи, приведенные к напряжению тяговой сети:
, приведенное к выпрямленному напряжению, а вместо действующих значений токов — выпрямленные токи, приведенные к напряжению тяговой сети: 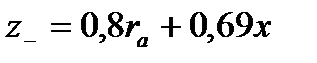 . Здесь
. Здесь 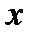 и
и 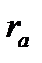 — соответственно индуктивная и активная составляющие полного сопротивления
— соответственно индуктивная и активная составляющие полного сопротивления 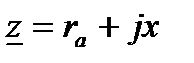 .
.
По формуле (5.10) можно определить потерю напряжения:
а) в контактной сети. При этом вместо 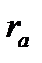 и
и 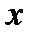 надо подставить для однопутного участка
надо подставить для однопутного участка 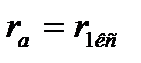 и
и 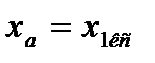 , воспользовавшись формулой для двухпутного
, воспользовавшись формулой для двухпутного 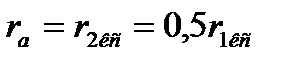 и
и 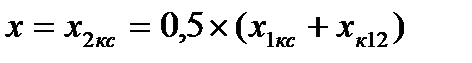 здесь согласно формуле
здесь согласно формуле 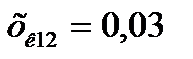 ;
;
б) в рельсовом пути. Для того чтобы учесть утечку токов из рельсов, следует вместо 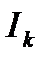 ввести
ввести 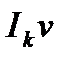 , здесь
, здесь  модуль того же значения,что и в формуле (5.25); и, кроме того, вместо
модуль того же значения,что и в формуле (5.25); и, кроме того, вместо 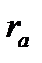 и
и 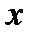 надо подставить для однопутного участка
надо подставить для однопутного участка 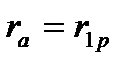 и
и 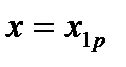 согласно формуле (5.19),для двухпутного
согласно формуле (5.19),для двухпутного 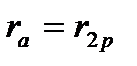 и
и 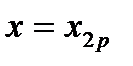 согласно формуле (5.28);
согласно формуле (5.28);
в) во всей тяговой сети в целом, т. е. в контактной сети и рельсах просто складываются потери в контактной сети и рельсах или вместо 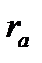 и
и 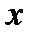 берут соответствующую сумму сопротивлений, а токи полностью. Для однопутного участка
берут соответствующую сумму сопротивлений, а токи полностью. Для однопутного участка 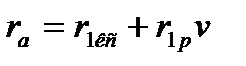 и
и 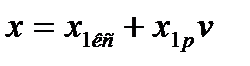 . Для двухпутного
. Для двухпутного 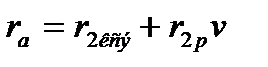 и
и 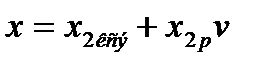 .
.
Как и для линий постоянного тока, потеря напряжения может быть представлена в виде суммы потерь согласно формулам (5.6) и (5.9) от своего тока и от токов остальных поездов и может быть выражена через входное активное и индуктивное сопротивление по выражению (5.7) и (5.10) и через активные и индуктивные составляющие передаточного сопротивления по формулам (5.8) и (5.11).
То же самое может быть сделано и для потери напряжения при выпрямительных электровозах. Характер изменения эпюр токов и потерь напряжения будет тот же, что на рис. 5.1.
Двухпутные (многопутные) участка о раздельным питанием проводов отдельных путей. Ток фидера отдельного пути или плеча подстанции определяют по тем же формулам (5.1) или (5.2).
Потери напряжения в контактной сети рассчитывают как для однопутного участка, а потери в рельсах — как для двухпутного или многопутного. Общая потеря напряжения равна их сумме.
Линии с двусторонним питанием. Однопутные участки и многопутные о параллельным соединением проводов отдельных путей. Определять нагрузки фидеров или плеч питания при напряжениях на подстанциях, равных по модулю и фазе, и при постоянном по длине сопротивлении можно так же, как и для постоянного тока, представив ток фидера или плеча питания в виде активной и реактивной составляющих. При этом нагрузки поездов также даются в виде активных и реактивных составляющих.
Тогда активная и реактивная составляющие тока фидера при плеча питания подстанции по аналогии с формулами (5.14) представятся следующими выражениями:
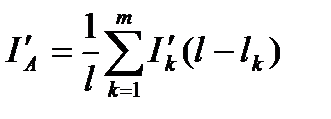 ; (5.13)
; (5.13)
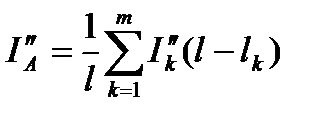 (5.14)
(5.14)
Полный ток фидера или плеча подстанции можно представить в виде
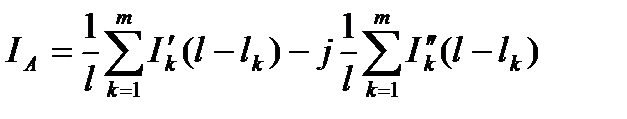 , (5.15)
, (5.15)
В частности, если у всех нагрузок угол  одинаков, то
одинаков, то
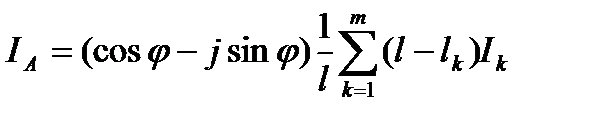 . (5.16)
. (5.16)
При определении тока фидера или плеча подстанции в формулы (5.13) - (5.16) вместо во множителя ( )войдет
)войдет 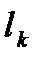 .
.
Потери напряжения в сети рассчитывают аналогично тому, как это делалось для постоянного тока.
По аналогии в формулой (5.21) или (5.22), определяющей потерю напряжения в сети до нагрузки  при постоянном токе, можно написать общую формулу и для однофазного переменного тока [в соответствии с формулой (5.10)]:
при постоянном токе, можно написать общую формулу и для однофазного переменного тока [в соответствии с формулой (5.10)]:
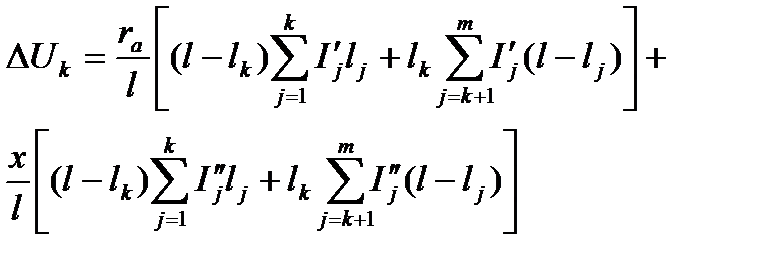 . (5.17)
. (5.17)
Или в другом виде
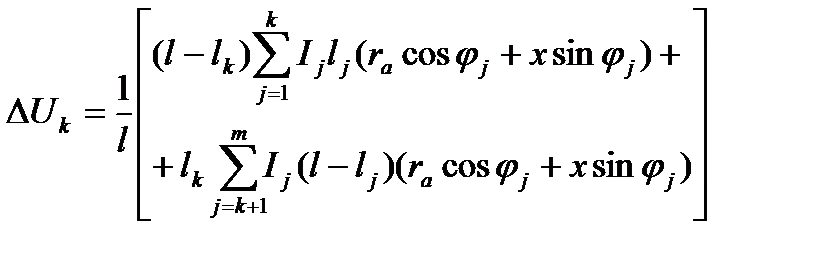 . (5.18)
. (5.18)
В частности, при равных углах сдвига фаз у всех нагрузок
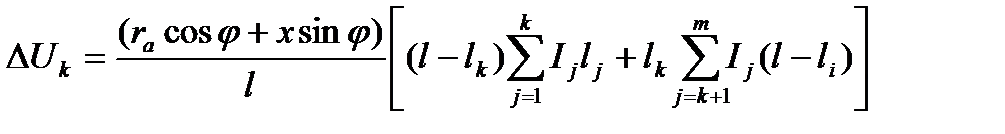 . (5.19)
. (5.19)
Потеря напряжения по формулам (5.18) - (5.19) может быть рассчитана в контактной сети, рельсовых путях и в целом в тяговой сети (контактная сеть и рельсовый путь). При этом надо вместо 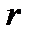 и
и 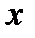 подставлять значения, приведенные выше для линий с односторонним питанием.
подставлять значения, приведенные выше для линий с односторонним питанием.
При различных напряжениях на подстанциях влияние уравнительного тока па потерю напряжения до нагрузки 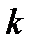 можно определить по формулам, выведенном для линий постоянного тока, но отдельно для активных составляющих тока
можно определить по формулам, выведенном для линий постоянного тока, но отдельно для активных составляющих тока 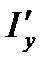 в активном сопротивлении
в активном сопротивлении 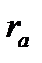 и для реактивных составляющих тока
и для реактивных составляющих тока 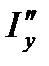 в реактивном сопротивлении
в реактивном сопротивлении  . Кроме того, потери напряжения имеют место и в сопротивлении системы и подстанции.
. Кроме того, потери напряжения имеют место и в сопротивлении системы и подстанции.
Отметим, что подобно тому, как это делалось при расчете потерь напряжения в линиях постоянного тока, потери напряжения в формулах (5.9) и (5.17) можно представить в виде двух слагаемых  и
и 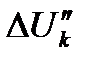 для однопутных участков и в виде трех слагаемых
для однопутных участков и в виде трех слагаемых 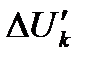 ,
, 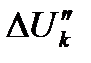 и
и 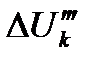 для многопутных участков. Формулы для
для многопутных участков. Формулы для 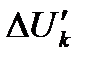 ,
, 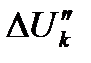 и
и 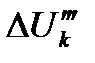 в случае однопутных участков и двухпутных с полным параллельным соединением путей будут аналогичны формулам при постоянном токе. Разница состоит в том, что взамен
в случае однопутных участков и двухпутных с полным параллельным соединением путей будут аналогичны формулам при постоянном токе. Разница состоит в том, что взамен 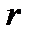 и
и 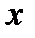 ,как и при одностороннем питании, подставляются приведенные там значения в зависимости оттого, что определяется: потеря напряжения в контактной сети, рельсах пли во всей тяговой сети, для синусоидального тока (первая гармоника) при для выпрямленного тока.
,как и при одностороннем питании, подставляются приведенные там значения в зависимости оттого, что определяется: потеря напряжения в контактной сети, рельсах пли во всей тяговой сети, для синусоидального тока (первая гармоника) при для выпрямленного тока.
Двухпутные (многопутные) участки с раздельным питанием проводов отдельных путей. Нагрузки фидеров и плеч подстанции определяют, как и для линий с параллельным соединением проводов, по формулам (5.13) - (5.16).
Особенности расчета потерь напряжения на двухпутном участке при раздельной работе путей заключаются в необходимости учета индуктивного влияния различных токов и контактных подвесок обоих путей друг на друга.
Однако примененный в гл. 2 принцип индуктивной развязки позволил учесть влияние токов тяговой сети одного пути на потери напряжения в сети другого через эквивалентное сопротивление рельсов.
Поэтому потерю напряжения 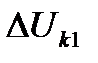 до нагрузки с номером
до нагрузки с номером 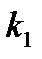 на первом пути двухпутного участка можно найти из выражения
на первом пути двухпутного участка можно найти из выражения
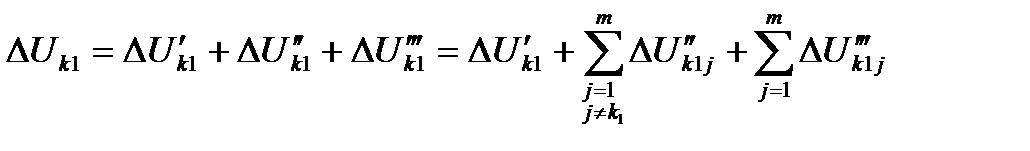 , (5.20)
, (5.20)
где 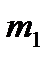 и
и 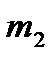 — число нагрузок соответственно на первом и втором путях;
— число нагрузок соответственно на первом и втором путях;
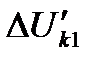 — потеря напряжения, вызванная нагрузкой рассматриваемогопоезда;
— потеря напряжения, вызванная нагрузкой рассматриваемогопоезда;
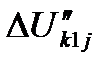 — потеря напряжения до рассматриваемого поезда, вызванная нагрузкой поезда
— потеря напряжения до рассматриваемого поезда, вызванная нагрузкой поезда  , расположенного па том же пути;
, расположенного па том же пути;
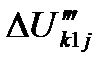 — то же но вызванная только в рельсах нагрузкой поезда
— то же но вызванная только в рельсах нагрузкой поезда 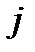 , расположенного на другом пути.
, расположенного на другом пути.
Если расчет ведут по первой гармонике тока, то 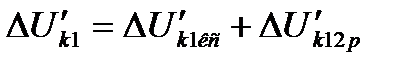 .В этом выражении
.В этом выражении
 ;
;
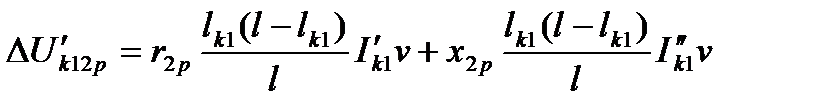 .
.
Откуда имеем
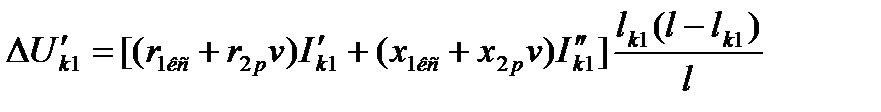 . (5.21)
. (5.21)
В формуле (5.20) потеря напряжения
 ,
,
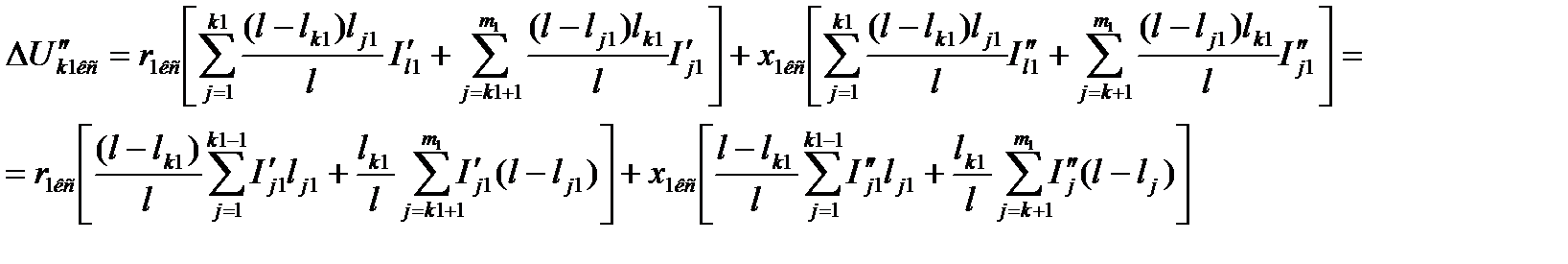 ;
;
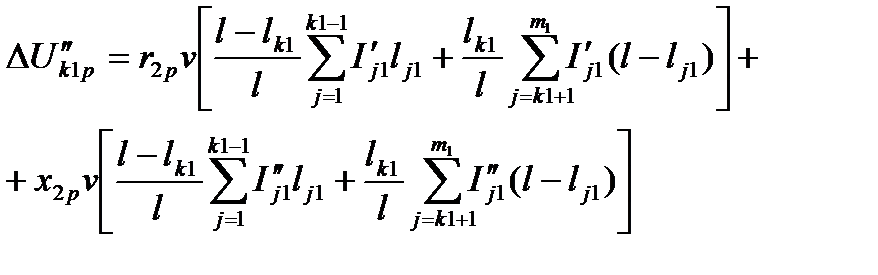 .
.
Следовательно, потеря напряжения:
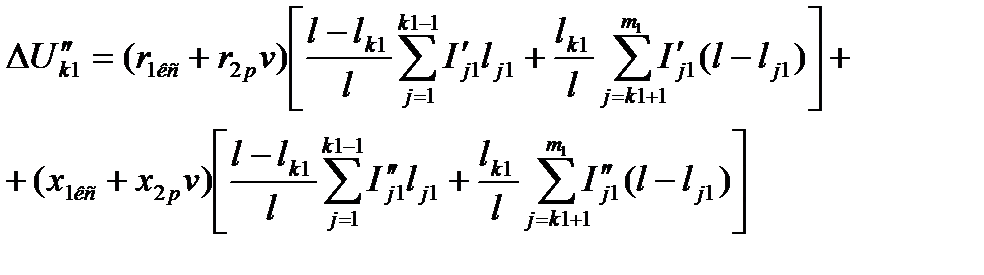 ; (5.22)
; (5.22)
 , (5.23)
, (5.23)
где 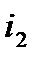 - номер тока второго пути, ближайшего к току
- номер тока второго пути, ближайшего к току 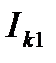 , при условии, что
, при условии, что
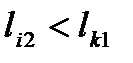 .
.
Если расчет ведут по выпрямленному току и эквивалентному сопротивлению 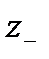 , то вместо формулы (5.21) получим выражение
, то вместо формулы (5.21) получим выражение
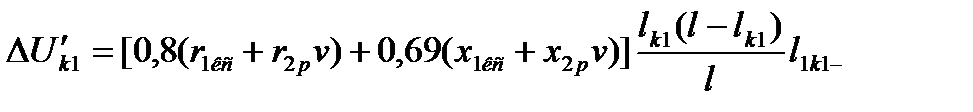 , (5.24)
, (5.24)
а вместо формулы (5.22) - выражения
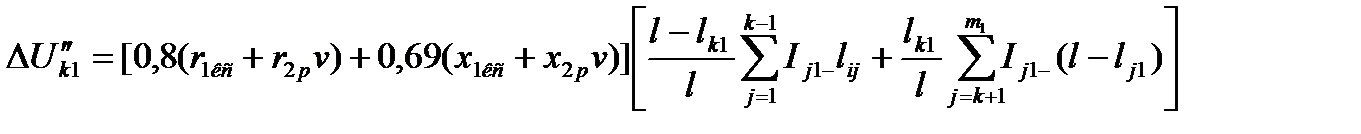 ; (5.25)
; (5.25)
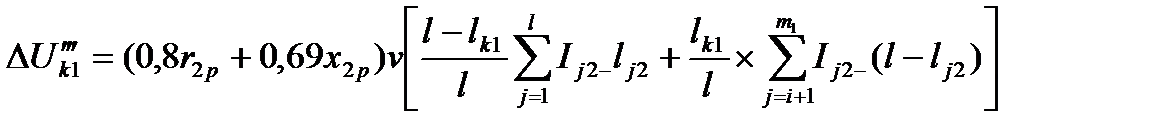 . (5.26)
. (5.26)
Двухпутные (многопутные) участки с узловой схемой питания. В данном случае контактная сеть первого и второго путей имеет не только индуктивную, но и гальваническую связь. Рассмотрим возможность применения к ней методов расчета токораспределения, применяемых при постоянном токе.
Пусть между подстанцией А и постом секционирования С на первом пути имеется нагрузка 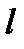 на расстоянии
на расстоянии 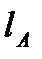 от подстанции А (рис. 5.2).
от подстанции А (рис. 5.2).
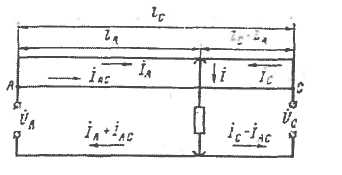
Рис. 5.2. К расчету потери напряжения на двухпутном участке переменного тока с постом секционирования
Определим, как распределяется эта нагрузка между фидерами подстанции А. Падения напряжения в сети первого и второго путей от А до С должны быть равны. Токи, протекающие по рельсам, оказывают одинаковое влияние па падение напряжения в проводах обоих путей. Поэтому при определении токораспределения нагрузки между проводами путей это влияние можно не принимать во внимание. Как и при постоянном токе, рассмотрим часть схемы на длине от подстанции А до поста секционирования С, условно заменив последний фиктивной подстанцией с некоторым напряжением 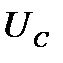 .Падение напряжения в проводах первого пути от А до С пропорционально выражению
.Падение напряжения в проводах первого пути от А до С пропорционально выражению
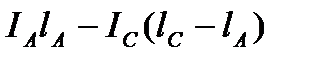 .
.
Электродвижущая сила влияния в сети второго пути, также пропорциональна этому выражению. Потеря напряжения по обоим путям равна 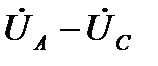 ,и она не изменится, если разложить ток
,и она не изменится, если разложить ток 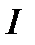 между точками А и С. Следовательно, нагрузку
между точками А и С. Следовательно, нагрузку 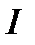 при расчетах узловой схемы можно распределять между точками А и С обратно пропорционально расстояниям до этих пунктов.
при расчетах узловой схемы можно распределять между точками А и С обратно пропорционально расстояниям до этих пунктов.
Таким образом, при узловой схеме, так же как и при более простых схемах постоянного и переменного тока, остается справедливым обычный способ распределения токов. Воспользовавшись этим, можно найти потерю напряжения до некоторой нагрузки 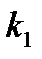 на первом пути:
на первом пути:
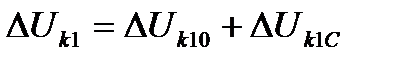 , (5.27)
, (5.27)
где 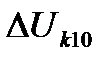 - потеря напряжения до
- потеря напряжения до 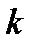 -го поезда при раздельной работе путей иналичии подстанции в точке С;
-го поезда при раздельной работе путей иналичии подстанции в точке С;
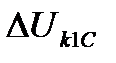 - составляющая потери напряжения до
- составляющая потери напряжения до  -го поезда от нагрузки подстанции в точке С, полученной в результате разноса всех токов между подстанцией и постом.
-го поезда от нагрузки подстанции в точке С, полученной в результате разноса всех токов между подстанцией и постом.
Величины 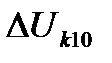 и
и 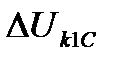 с можно рассчитывать по формулам (5.37)-(5.40).
с можно рассчитывать по формулам (5.37)-(5.40).
Если расчет ведут для синусоидальных токов, то, подставив в формулы (5.37) - (5.40) вместо 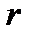 активную составляющую сопротивления контактной сети
активную составляющую сопротивления контактной сети 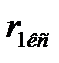 и вместо
и вместо 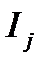 активную составляющую тока, т. е.
активную составляющую тока, т. е. 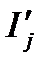 , получим первую составляющую потери напряжения в контактной, сети. Затем, заменив в этих же формулах
, получим первую составляющую потери напряжения в контактной, сети. Затем, заменив в этих же формулах 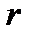 на
на 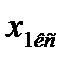 и
и  на реактивную составляющую
на реактивную составляющую 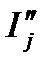 , получим вторую составляющую потери напряжения в контактной сети. Сумма этих двух составляющих и даст значение потерн напряжения в контактной сети.
, получим вторую составляющую потери напряжения в контактной сети. Сумма этих двух составляющих и даст значение потерн напряжения в контактной сети.
Потерю напряжения в рельсах следует определять так же, как и в предыдущих схемах, так как они между собой соединены параллельно.
Если же расчет ведут по выпрямленному току и эквивалентному сопротивлению, то вместо 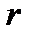 в формулы (5.37) - (5.40) следует подставить
в формулы (5.37) - (5.40) следует подставить 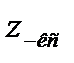 , как и при раздельном питании проводов отдельных путей и при определении потери напряжения в рельсах
, как и при раздельном питании проводов отдельных путей и при определении потери напряжения в рельсах 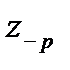 , т. е. так же, как и при раздельном питании проводов отдельных путей.
, т. е. так же, как и при раздельном питании проводов отдельных путей.
Если уровни и фазы напряжений подстанций различны и не зависят от тяговой нагрузки, то, как и для линий постоянного тока, следует к 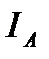 добавить (геометрически) уравнительный ток
добавить (геометрически) уравнительный ток 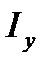 и вычесть его из
и вычесть его из 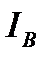 (также, конечно, геометрически). Уравнительный ток
(также, конечно, геометрически). Уравнительный ток 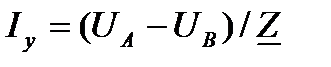 . Здесь
. Здесь 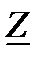 — полное сопротивление фидерной зоны АВ.
— полное сопротивление фидерной зоны АВ.
Напряжения на смежных подстанциях могут различаться по модулю вследствие различного коэффициента трансформации на подстанциях (при регулировании напряжения), а также по модулю и углу сдвига фаз ввиду падения напряжения в линии передачи, питающей эти подстанции, пли вследствие разности напряжения в точках присоединения тяговых подстанций к электроэнергосистеме. Как будет подробно показано в п. 5.11, различие напряжений по модулю приводит к появлению реактивного уравнительного тока, а различие по углу — к появлению активного уравнительного тока. С достаточным приближением можно по отдельности наложить эти уравнительные токи на активные и реактивные нагрузки, определяемые по формулам (5.13) - (5.16).
Date: 2015-07-24; view: 1072; Нарушение авторских прав