
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические указания к контрольной работе
|
|
УДК 658.5
Теория принятия решений: Методические указания и задания к контрольной работе для студентов заочной формы обучения по направлению бакалавр экономики. – Вологда: ВоГТУ, 2010. – 8 с.
В методических указаниях изложены методы принятия решений в различных ситуациях. Методические указания содержат варианты контрольной работы для студентов заочной формы обучения по специальности бакалавр экономики.
Утверждено редакционно-издательским советом ВоГТУ
Составитель: Матвеев Н.С., канд.физ.-мат.наук, доцент
Рецензент: Клещ С.А., канд.экон.наук, доцент
Среди множества проблем современного менеджмента важнейшими являются разработка, принятие и осуществление управленческого решения, представляющего собой основной инструмент управляющего воздействия. Проблема имеет важное прикладное значение, которое возрастает по мере усложнения хозяйственных ситуаций и управленческих задач, требующих решения.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
Целью контрольной работы по теории принятия решений (ТПР) является овладение принципами разработки и принятия оптимальных решений, а также методикой количественной оценки их эффективности.
Теоретически существует три типа ситуаций, в которых принимаются решения, в условиях:
1. Определенности, когда имеется точная информация по всем параметрам проблемы – используются различные методы оптимизации.
2. Риска (вероятности наступления состояний природы известны).
3. Неопределенности (информация о вероятностях наступления состояний природы отсутствует).
Каждый вариант контрольной работы включает 4 задачи по наиболее важным разделам курса.
Задача 1 предполагает изучение темы «Экспертные оценки». Экспертные оценки – количественные или иные оценки характеристик объектов, неподдающихся непосредственному измерению. Для решения задачи используется метод парных сравнений (МПС): все объекты попарно сравниваются и устанавливается, какой важнее. В МПС используется следующая шкала предпочтений:
если 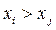 , то фактор
, то фактор 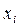 предпочтительнее фактора
предпочтительнее фактора 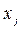 ;
;
если 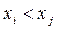 , то фактор
, то фактор 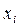 менее предпочтителен фактора
менее предпочтителен фактора 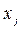 ;
;
если 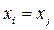 , то фактор
, то фактор 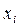 и фактор
и фактор 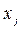 равнозначны. Рекомендуется выбрать степень предпочтения факторов R=3.
равнозначны. Рекомендуется выбрать степень предпочтения факторов R=3.
Строится матрица А с элементами:
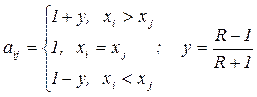
Находим вектор-столбец P с элементами 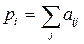 . Для определения веса (значимости) каждого фактора проводим операцию нормализации:
. Для определения веса (значимости) каждого фактора проводим операцию нормализации:
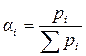 .
.
Замечание: точность вычислений – 0,001.
Для решения задачи 2 следует изучить тему «Принятие решений в условиях риска», когда вероятности наступления состояний природы известны. Решение принимается при помощи критерия Байеса. Выбирается тот вариант, для которого средний выигрыш максимален:
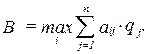
Предельная цена информации о риске определяется как разность между математическим ожиданием выплаты, соответствующее идеальной информации, и математическим ожиданием, которое мы получаем при обычной ситуации.
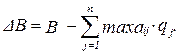
Задача 3 предполагает принятие решения в ситуации неопределенности, когда информация о вероятностях наступления состояний природы отсутствует.
Для принятия решения в условиях неопределенности используются следующие критерии:
1. Максиминный критерий Вальда (пессимизма).
Выбирается тот вариант, при котором минимальный выигрыш максимален:
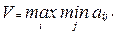
2. Критерий сверхоптимизма.
Выбирается вариант, обеспечивающую максимальный выигрыш среди максимально возможных, т.е.
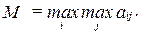
3. Критерий оптимизма – пессимизма Гурвица.
Выбирается вариант, максимизирующий линейную комбинацию максимального и минимального выигрышей:
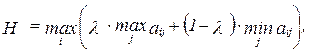
где 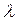 – степень оптимизма
– степень оптимизма 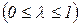 . Рекомендуется выбрать
. Рекомендуется выбрать 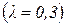 .
.
4. Критерий минимаксного риска Сэвиджа.
Сначала строится по столбцам так называемая «матрица рисков», элементы которой определяются по формулам:
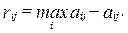
По критерию Сэвиджа лучший вариант тот, который обеспечивает минимальное значение максимального риска:
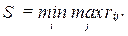
Замечание: при решении задачи следует пользоваться таблицей:
| Вариант | П1 | П2 | П3 | П4 | П5 | V | М | Н |
| А1 | ||||||||
| А2 | ||||||||
| А3 | ||||||||
| max |
Окончательно, в качестве оптимального выбирается тот вариант, который чаще встречается как оптимальный по этим четырем критериям.
Задача 4 соответствует принятию сложного решения, когда необходимо учитывать несколько различных по размерности показателей. В этом случае используют интегральные показатели с весами, применяемыми к безразмерным величинам. Эти величины определяются по формулам:
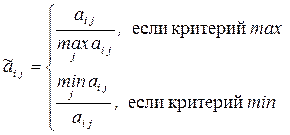
Тогда интегральный критерий имеет вид:
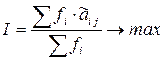
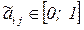 .
.
Составляется таблица, например, для варианта контрольной работы №9:
| № фактора | Факторы | ¯ | Значения по вариантам, 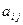
| Нормированное значение, 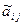
| Веса, 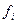
| ||||
| Затраты | Min | ||||||||
| Время реализации | Min | ||||||||
| Качество | Max | ||||||||
| Сумма |
Вычисляется по каждому варианту интегральный критерий, где веса берутся из решения задачи 1. В качестве оптимального решения выбирается тот вариант, для которого интегральный критерий имеет максимальное значение.
Date: 2015-07-24; view: 329; Нарушение авторских прав