Определение. Поверхностный интеграл называется потоком векторного поля через поверхность D

Если поверхность разбита на конечное число частичных поверхностей, то поток векторного поля через всю поверхность будет равен сумме потоков через частичные поверхности.

Если преобразовать скалярное произведение в координатную форму, то получаем соотношение:

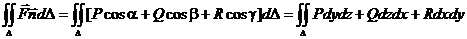
Если на области D существует функция f(x, y, z), имеющая непрерывные частные производные, для которых выполняются свойства:

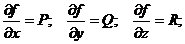
то такую функцию называют потенциальной функцией или потенциалом вектора .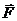

Тогда вектор 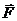является градиентом функции f.

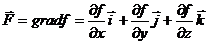
Потенциал может быть найден по формуле:

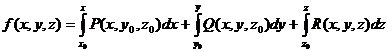
В этой формуле x₀, y₀, z₀ – координаты некоторой начальной точки. В качестве такой точки удобно брать начало координат.

Теорема. Для того, чтобы поле вектора 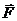, заданного в некоторой области, имело потенциал, необходимо и достаточно, чтобы выполнялось одно из двух условий:

1) Интеграл от вектора 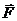по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.

2) Интеграл по любому кусочно – гладкому пути, соединяющему две любые точки поля не зависит, от пути интегрирования.

Формула Стокса.

Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.

Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.

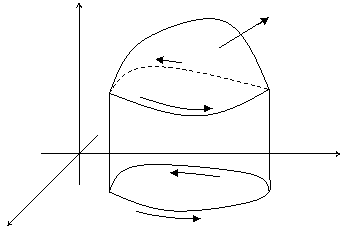
z S

L

y

D

l

x

Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.

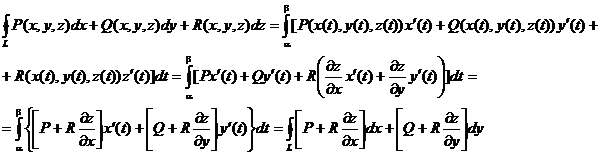
Введем обозначения:

Применив формулу Грина – Остроградского, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:

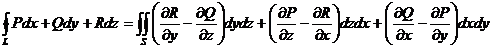
эта формула и называется формула Стокса.

Определение. Вектор 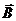, компоненты которого равны соответственно равны

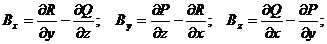
называется вихрем или ротором вектора 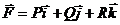и обозначается:

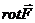
Определение. Символический вектор 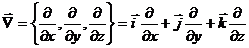называется оператором Гамильтона. (Уильям Роуан Гамильтон (1805 – 1865) – ирландский математик) Символ Ñ - “набла”.

С учетом этого обозначения можно представить себе понятие ротора вектора 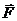как векторного произведения оператора Гамильтона на вектор .

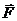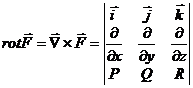
Определение. Криволинейный интеграл, представляющий собой работу векторного поля вдоль некоторой кривой L называется линейным интегралом от вектора 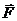по ориентированной кривой L.

Если кривая L представляет собой замкнутый контур, то линейный интеграл по такому контуру называется циркуляцией вектроного поля 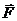вдоль контура L.

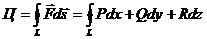
В векторной форме теорему Стокса можно сформулировать так:

Циркуляция вектора вдоль контура некоторой поверхности равна потоку вихря (ротора) через эту поверхность.

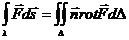
Отметим, что рассмотренная выше формула Грина – Остроградского является частным случаем формулы Стокса.

Также при условии равенства нулю всех компонент ротора вектора, получаем, что криволинейный интеграл по любой пространственной кривой равен нулю, т.е. криволинейный интеграл не зависит от пути интегрирования.

Определение. Выражение 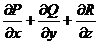называется дивергенцией вектора (дивергенцией векторной функции) 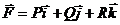и обозначается

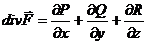
Таким образом, формулу Гаусса – Остроградского может быть записана в виде:

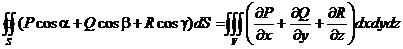
или

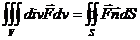
т.е. интеграл от дивергенции векторного поля 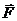по объему равен потоку вектора через поверхность, ограниченную этим объемом.

Определение. Векторное поле 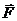называется соленоидальным (трубчатым), если div 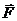=0.

C помощью описанного выше оператора Гамильтона можно представить определенные нами понятия следующим образом:

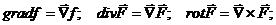
Как было сказано выше (См. Уравнение Лапласа.), выражение

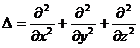
называется оператором Лапласа.

Справедливы следующие соотношения:

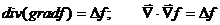
Справедливость этих равенств легко проверить непосредственной подстановкой.

Теперь рассмотрим примеры применения рассмотренных выше понятий.

Date: 2015-07-22; view: 371; Нарушение авторских прав