
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача № 12
|
|
Решение. Все вычисления будем заносить в таблицу.
Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
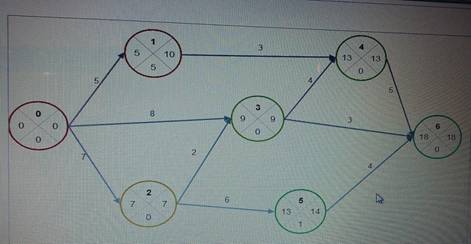
При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).
Расчет сроков свершения событий.
Для i=1 (начального события), очевидно tp()=0.
i=1: tp(1) = tp(0) + t(0,1) = 0 + 5 = 5.
i=2: tp(2) = tp(0) + t(0,2) = 0 + 7 = 7.
i=3: max(tp(0) + t(0,3);tp(2) + t(2,3)) = max(0 + 8;7 + 2) = 9.
i=4: max(tp(1) + t(1,4);tp(3) + t(3,4)) = max(5 + 3;9 + 4) = 13.
i=5: tp(5) = tp(2) + t(2,5) = 7 + 6 = 13.
i=6: max(tp(3) + t(3,6);tp(4) + t(4,6);tp(5) + t(5,6)) = max(9 + 3;13 + 5;13 + 4) = 18.
Длина критического пути равна раннему сроку свершения завершающего события 6: tkp=tp(6)=18
При определении поздних сроков свершения событий tп(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).
Для i=6 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): tп(8)= tр(8)=18
Рассмотрим события:
(3,6): 12
(4,6): 18
(5,6): 17
Максимальное значение: 18. Записываем его в графу 7 по всем строчкам, оканчивающимся на номер последнего события 6.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
i=4: tп(4) = tп(6) - t(4,6) = 18 - 5 = 13.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 5.
i=5: tп(5) = tп(6) - t(5,6) = 18 - 4 = 14.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
i=3: min(tп(4) - t(3,4);tп(6) - t(3,6)) = min(13 - 4;18 - 3) = 9.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 4.
i=4: tп(4) = tп(6) - t(4,6) = 18 - 5 = 13.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 3.
i=3: min(tп(4) - t(3,4);tп(6) - t(3,6)) = min(13 - 4;18 - 3) = 9.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 2.
i=2: min(tп(3) - t(2,3);tп(5) - t(2,5)) = min(9 - 2;14 - 6) = 7.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 1.
i=1: tп(1) = tп(4) - t(1,4) = 13 - 3 = 10.
Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 0. Для определения графы 7 этих строк просматриваются все строчки, начинающиеся с номера 0.
i=0: min(tп(1) - t(0,1);tп(2) - t(0,2);tп(3) - t(0,3)) = min(10 - 5;7 - 7;9 - 8) = 0.
| Номер события | Сроки свершения события: ранний tp(i) | Сроки свершения события: поздний tп(i) | Резерв времени, R(i) |
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 3, затем с номера 1 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (3,4) в графу 1 поставим число 2, т.к. на номер 3 оканчиваются 2 работы: (0,3),(2,3).
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 2, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4.
Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк.
Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Графы 6 и 7 заполняются обратным ходом, т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)).
Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5.
Анализ сетевой модели по времени
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tijР.Н. | Ранние сроки: окончание tijР.О. | Поздние сроки: начало tijП.Н. | Поздние сроки: окончание tijП.О. | Резервы времени: полный tijП | Резервы времени: свободный tijС.В. | Резервы времени: событий Rj |
| (0,1) | |||||||||
| (0,2) | |||||||||
| (0,3) | |||||||||
| (1,4) | |||||||||
| (2,3) | |||||||||
| (2,5) | |||||||||
| (3,4) | |||||||||
| (3,6) | |||||||||
| (4,6) | |||||||||
| (5,6) |
Примечание.
а) графы 1 и 3 заполняются на основе исходных данных.
б) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
г) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
г) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
д) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
е) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
ж) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
з) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
и) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.
Критический путь: (0,2)(2,3)(3,4)(4,6)
Продолжительность критического пути: 18
Анализ сетевого графика
Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:
Kc = npab / ncob
где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед.
Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.
Kc = 10 / 7 = 1.43
Поскольку Kc < 1.5, то сетевой график является простым.
Коэффициентом напряженности КH работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:
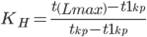
где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j, от начала до конца сетевого графика; tkp – продолжительность (длина) критического пути; t1kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.
Коэффициент напряженности КH работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности КH работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.
| Работа | Путь | Максимальный путь, t(Lmax) | Совпадающие работы | t1kp | Расчет | КH |
| (0,1) | (0,1)(1,4)(4,6) | (4,6) | (13-5)/(18-5) | 0.62 | ||
| (0,2) | (0,2)(2,3)(3,4)(4,6) | (0,2)(2,3)(3,4)(4,6) | (18-18)/(18-18) | |||
| (0,3) | (0,3)(3,4)(4,6) | (3,4)(4,6) | (17-9)/(18-9) | 0.89 | ||
| (1,4) | (0,1)(1,4)(4,6) | (4,6) | (13-5)/(18-5) | 0.62 | ||
| (2,3) | (0,2)(2,3)(3,4)(4,6) | (0,2)(2,3)(3,4)(4,6) | (18-18)/(18-18) | |||
| (2,5) | (0,2)(2,5)(5,6) | (0,2) | (17-7)/(18-7) | 0.91 | ||
| (3,4) | (0,2)(2,3)(3,4)(4,6) | (0,2)(2,3)(3,4)(4,6) | (18-18)/(18-18) | |||
| (3,6) | (0,2)(2,3)(3,6) | (0,2)(2,3) | (12-9)/(18-9) | 0.33 | ||
| (4,6) | (0,2)(2,3)(3,4)(4,6) | (0,2)(2,3)(3,4)(4,6) | (18-18)/(18-18) | |||
| (5,6) | (0,2)(2,5)(5,6) | (0,2) | (17-7)/(18-7) | 0.91 |
Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).
Date: 2015-07-23; view: 713; Нарушение авторских прав