
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Найти производные сложных функций. Министерство образования и науки
|
|
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Функции нескольких переменных.
Индивидуальные задания.
Волгодонск
УДК 811.111-36 (076.5)
Рецензент д.т.н., проф. Сысоев Ю.С.
Шпонарская С.Н., Столяр Л.Н., Кремлев А.Г. Функции нескольких переменных. Индивидуальные задания: учеб.-метод. пособие/ С.Н. Шпонарская, Л.Н. Столяр, А.Г. Кремлев. – Волгодонский инженерно-технический институт (ф) НИЯУ МИФИ.
Предназначено для студентов 1-го курса всех специальностей.
© ВИТИ НИЯУ МИФИ, 2011
© Коллектив авторов, 2011
Найти полный дифференциал первого порядка функции двух переменных.
1. 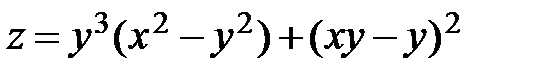 ; ;
| 2. 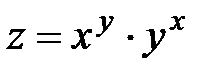 ; ;
|
3. 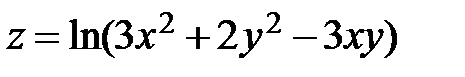 ; ;
| 4. 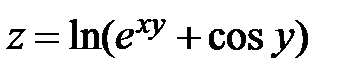 ; ;
|
5. 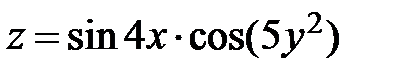 ; ;
| 6.  ; ;
|
7. 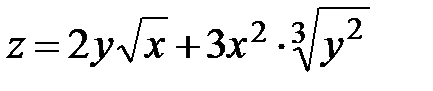 ; ;
| 8. 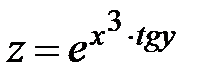 ; ;
|
9. 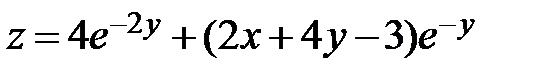 ; ;
| 10. 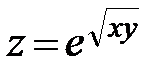 ; ;
|
11. 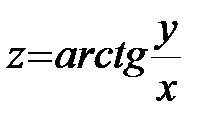 ; ;
| 12.  ; ;
|
13. 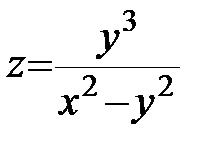 ; ;
| 14.  ; ;
|
15. 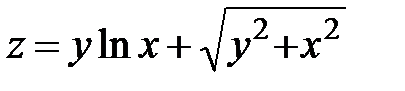 ; ;
| 16. 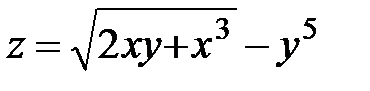 ; ;
|
17. 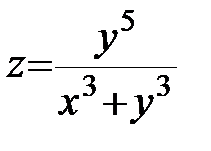 ; ;
| 18. 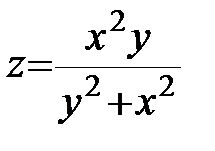 ; ;
|
19. 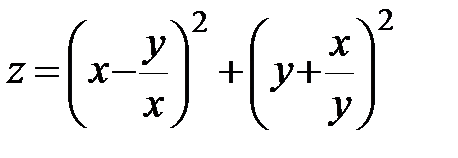 ; ;
| 20. 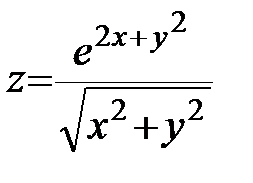 ; ;
|
21. 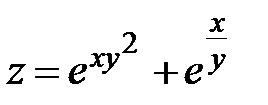 ; ;
| 22. 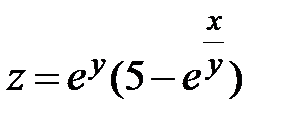 ; ;
|
23. 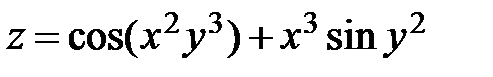 ; ;
| 24. 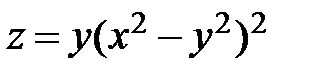 ; ;
|
25. 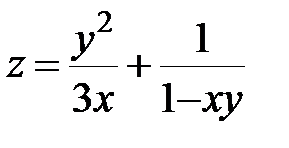 ; ;
| 26. 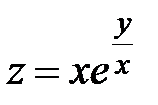 ; ;
|
27. 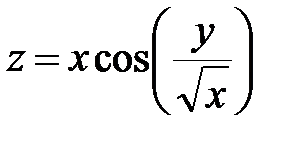 ; ;
| 28. 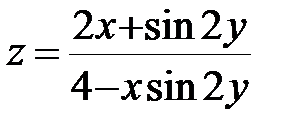 ; ;
|
29. 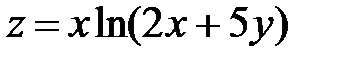 ; ;
| 30. 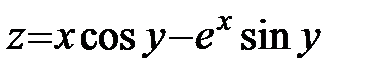 . .
|
Найти производные сложных функций.
1. 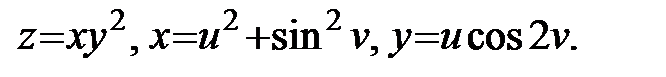 Найти
Найти 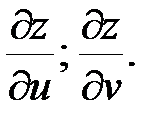
2. 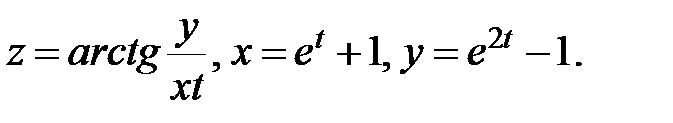 Найти
Найти 
3. 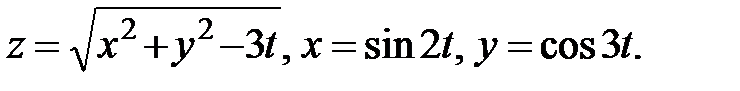 Найти
Найти 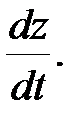
4. 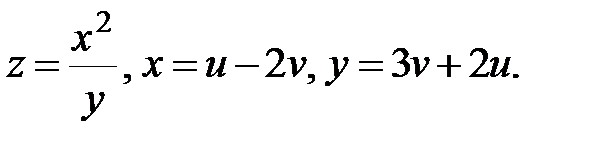 Найти
Найти 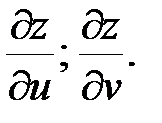
5. 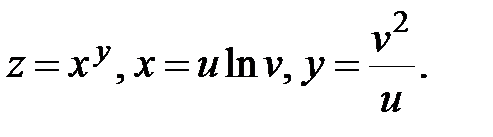 Найти
Найти 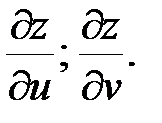
6. 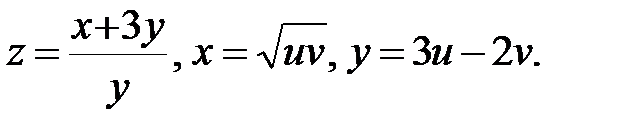 Найти
Найти 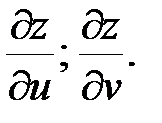
7. 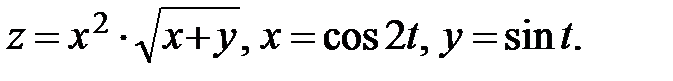 Найти
Найти 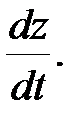
8. 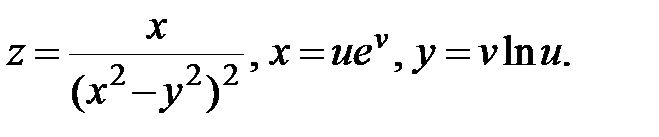 Найти
Найти 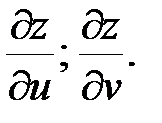
9. 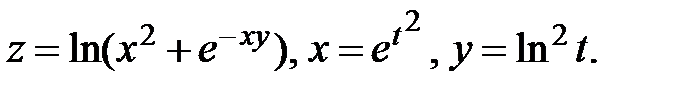 Найти
Найти 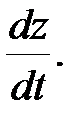
10. 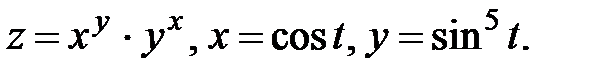 Найти
Найти 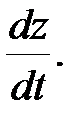
11. 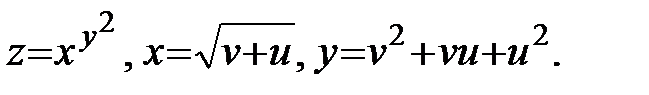 Найти
Найти 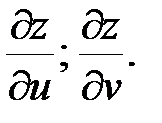
12. 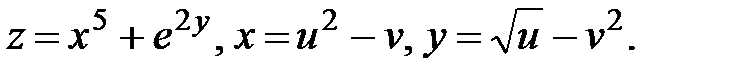 Найти
Найти 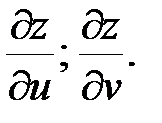
13. 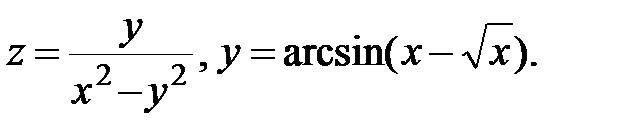 Найти
Найти 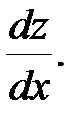
14. 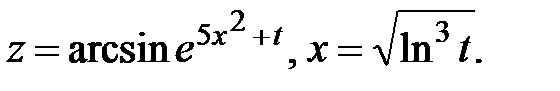 Найти
Найти 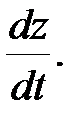
15. 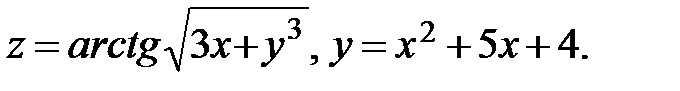 Найти
Найти 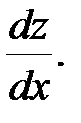
16. 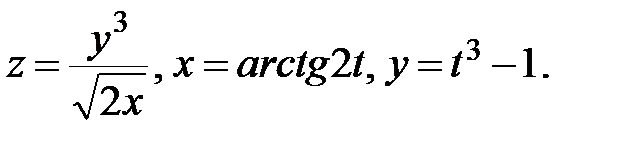 Найти
Найти 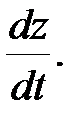
17. 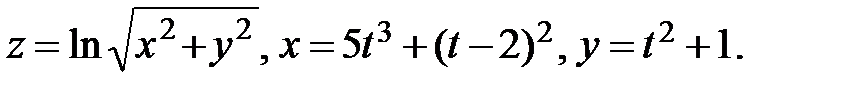 Найти
Найти 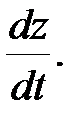
18. 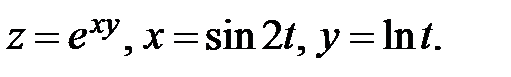 Найти
Найти 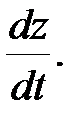
19. 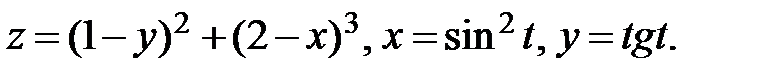 Найти
Найти 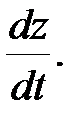
20. 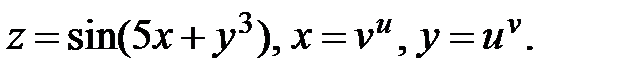 Найти
Найти 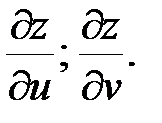
21. 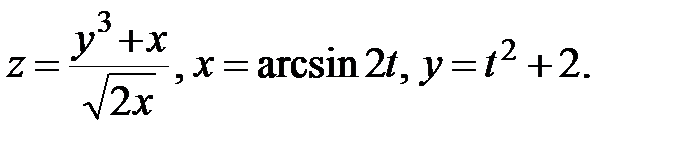 Найти
Найти 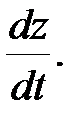
22. 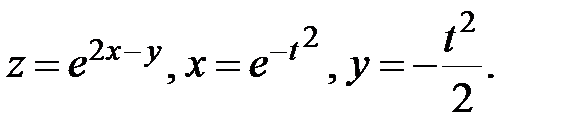 Найти
Найти 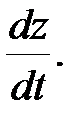
23.  Найти
Найти 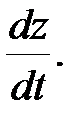
24. 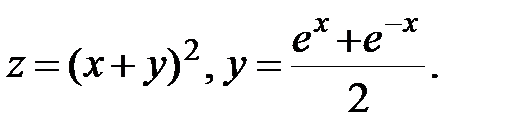 Найти
Найти 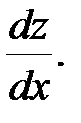
25.  Найти
Найти 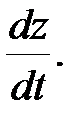
26. 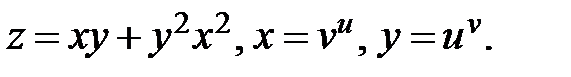 Найти
Найти 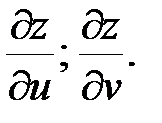
27. 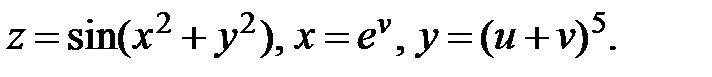 Найти
Найти 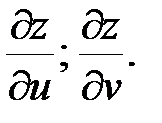
28. 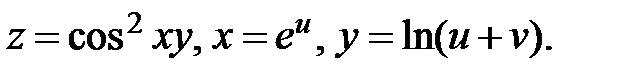 Найти
Найти 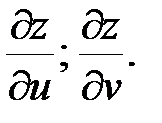
29. 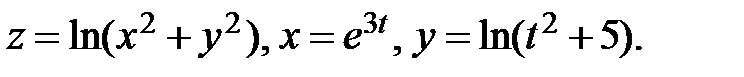 Найти
Найти 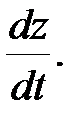
30.  Найти
Найти 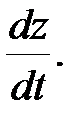
Date: 2015-07-22; view: 334; Нарушение авторских прав