Построение двойственной задачи к задаче об оптимальном выпуске продукции. Каждой ЗЛП можно определённым образом сопоставить некоторую другую задачу, называемую двойственной (или сопряжённой) по отношению к исходной задаче

Каждой ЗЛП можно определённым образом сопоставить некоторую другую задачу, называемую двойственной (или сопряжённой) по отношению к исходной задаче.

Рассмотрим пример, показывающий, как в реальной экономичес­кой ситуации появляются взаимно двойственные задачи линейного программирования. На некотором предприятии после выполнения годового плана возник вопрос – как поступить с остатками сырья? У руководства и экономистов предприятия возникли два пути решения: либо продать остатки сырья какой-нибудь нуждающейся в нем организации (наиболее простой вариант), либо наладить из оставшегося сырья производство каких-то изделий на своем собственном оборудовании.

Для простоты будем считать, что имеются два вида сырья S ₁ и S ₂, остатки которого составляют соответственно 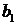и 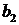единиц. Из этого сырья можно наладить производство трех видов товаров: Т ₁, Т ₂, Т ₃. От реализации одной единицы каждого вида товара Т ₁, Т ₂, Т ₃ предприятие полу­чит прибыль соответственно , , у.е. Нормы расхода сырья на производство товаров Т ₁, Т ₂, Т ₃ вместе с данными о при­были и запасах представлены в следующей таблице, где означает, сколько единиц сырья расходуется на производство товара .

Виды товаров	S 1	S 2	Прибыль
Т 1
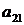
Т 2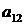
Т 3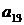
Запасы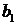

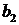
Проследим за ходом мыслей экономистов предприятия. Как уже гово­рилось, им предстояло проанализировать две возможности.

При исследовании второй возможности (наладить выпуск товаров Т ₁, Т ₂, Т ₃) возникает вопрос о плане выпуска товаров. План выпуска задается тремя числами 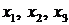, где 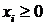– количество единиц товара , которое следует произвести (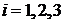). Неизвестные 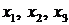должны удовлетворять системе ресурсных ограничений

(3.2)

причем прибыль, которую получит предприятие от реализации оптимального плана выпуска товаров, должна быть максимальной:

. (3.3)

Следо­вательно, чтобы наилучшим образом использовать вторую возможность, нужно решить задачу линейного программирования (3.2), (3.3).

Исследуем теперь первую возможность – продать сырье другой организации. Здесь возникает вопрос: по каким ценам продавать сырье? Обозначим эти цены 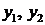, где 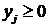– цена единицы сырья S _i ().

Справедливое требование к ценам со стороны продающего пред­приятия состоит в следующем. Если взять сырье, идущее на изготов­ление единицы товара Т_i (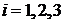), то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – лучше изго­товить из него товар и получить за него прибыль). Это требование приводит к системе неравенств

(3.4)

Первое из написанных неравенств в системе (3.4) означает, что вы­ручка от продажи единиц сырья S ₁ и 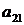единиц сырья S ₂ (именно такое количество сырья расходуется на изготовление единицы товара T ₁) не мень­ше, чем прибыль, которую могло бы получить предприятие от про­дажи единицы товара T ₁, если бы оно отказалось от идеи продать сырье и занялось изготовлением из него товаров T ₁, T ₂, T ₃. Анало­гичный смысл имеют остальные два неравенства.

Что же касается покупателя, то для него единствен­ное пожелание заключается в сокращении до минимума расходов на покупку сырья:

. (3.5)

Итак, для оптимального использования первой воз­можности необходимо решить задачу линейного программирования (3.4), (3.5).

Для наглядности сопоставим формулировки двух задач:

Задача (3.2), (3.3)	Задача (3.4), (3.5)
()	(),

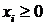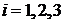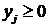Date: 2015-07-23; view: 335; Нарушение авторских прав