Общие сведения

СОГЛАСОВАНО УТВЕРЖДАЮ

Зав. кафедрой ОПНН, доцент Зам. директора по учебной работе,

______________Н.М. Захаров _______________Ф.М. Хазиев

______________ _______________

Методические указания к лабораторной работе № 3

Построение линий энергии и потенциальной энергии

Дисциплина "Процессы и аппараты химической технологии.

Часть I – Гидравлика"

СОГЛАСОВАНО РАЗРАБОТАЛ

Инженер по охране труда Доцент кафедры ОПНН

_____________Г.В. Мангуткина ______________Р.Г. Худайдатов

_____________ ______________

Салават

Изложена физическая сущность построения линий энергии и теория расчета по уравнению Бернулли. Приведены инструкции по выполнению лабораторной работы по дисциплине "Процессы и аппараты химической технологии. Часть I – Гидравлика".

Методические указания предназначены: для студентов специальности 240801 "Машины и аппараты химических производств", 240403 "Химическая технология природных энергоносителей и углеродных материалов"; для студентов-бакалавров направления 241000 «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии», профиль "Машины и аппараты химических производств"; направления 240100 «Химическая технология», профиль "Химическая технология природных энергоносителей и углеродных материалов" всех форм обучения.

© Филиал ФГБОУ ВПО Уфимского государственного нефтяного технического

Университета в г. Салавате 2012.

Лабораторная работа № 3 (2 часа)

Построение линий энергии и потенциальной энергии

Цель работы:Построить пьезометрическую и напорную линию по опытным данным для трубопровода переменного сечения. Изучить, как изменяются удельная потенциальная, удельная кинетическая энергия и полная удельная энергия по длине трубопровода в зависимости от изменения живого сечения.

Общие сведения

Жидкость, движущаяся в поле силы тяжести, обладает механической энергией, составляющими являются удельная потенциальная энергия положения Z, удельная потенциальная энергия давления и удельная кинетическая энергия 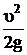(удельной называется энергия, приходящаяся на единицу веса жидкости).

Для струйки невязкой жидкости сумма кинетической и потенциальной энергий есть величина постоянная, т.е.

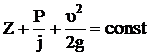. (1)

Это уравнение называется уравнением Бернулли. Оно представляет собой закон сохранения механической энергии.

Величина Z называется нивелирной высотой. Она определяется расстоянием по вертикали от плоскости сравнения до центра тяжести рассматриваемого сечения. Величина , имеющая размерность длины называется пьезометрической высотой. Она представляет собой высоту столба жидкости, вес которого при атмосферном давлении на его свободной поверхности уравновешивает силу давления в центре тяжести рассматриваемого сечения. Величина 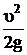, также размерность длины, называется высотой скоростного напора. Это высота, на которую может подняться над рассматриваемым сечением жидкость, начавшая движение с вертикально направленной скоростью u при отсутствии сопротивлений её движению.

Сумма трёх высот: нивелирной, пьезометрической и скоростного напора называется гидродинамическим напором (Н). В потоке невязкой жидкости гидродинамический напор является величиной, постоянной по длине потока.

При давлении вязкой жидкости энергия потока не остается постоянной. Она уменьшается от сечения к сечению по мере продвижения жидкости. Потери энергии возникают из-за внутреннего трения и перемешивания. Если рассматривать два сечения потока жидкости при установившемся движении: I–I и II–II (рисунок 1) то гидродинамический напор во втором сечении всегда меньше, чем в первом, на величину потерь h_1,2.

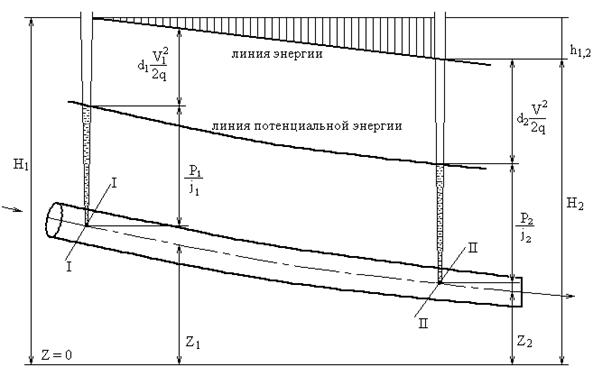
Рисунок 1 – Линии энергии

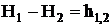(2)

или

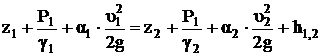, (3)

где u₁ – средняя скорость в i-м сечении.

Таким образом, для вязкой жидкости уравнение (3) представляет собой уравнение баланса энергии. Уравнение Бернулли в виде формулы (3) справедливо для установившегося течения вязкой несжижаемой жидкости при параллельно струйном или плавно изменяющемся движении, когда контрольное сечение можно считать плоским. При этом имеется в виду, что между контрольными сечениями нет ни источника, ни стока энергии.

Так как скорости частиц жидкости по сечению потока неодинаковы, то высота скоростного напора по живому сечению потока меняется. При определении действительной кинетической энергии в данном сечении потока этот факт учитывается безразмерным коэффициентом a (коэффициентом Кориолиса), зависящим от распределения скоростей в живом сечении потока. Физический смысл коэффициента Кориолиса заключается в том, что он представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при том же расходе, если бы все частицы жидкости обладали одинаковыми скоростями, равными средней скорости u.

При ламинарном движении в прямой круглой трубе профиль скорости имеет вид параболоида вращения, в этом случае a = 2. При турбулентном движении вследствие интенсивного перемешивания профиль скорости в сечении более равномерен и a = 1,13 ¸ 1,15.

На рисунке 1 можно наметить ряд линий, характеризующих движение жидкости. Если мы соединим уровни жидкости в пьезометрах, установленных вдоль потока, получим линию потенциальной энергии, показывающую изменение потенциальной энергии потока относительно произвольно взятой плоскости сравнения.

Соединив гидродинамические напоры в различных сечениях, получим линию энергии, показывающую изменение удельной энергии жидкости вдоль по потоку относительно той же плоскости сравнения.

Расстояние по вертикали между уровнем первоначальной энергии и линией энергии равно потере энергии на пути от сечения I–I до сечения II–II.

Энергия h_1,2, теряемая жидкостью на участке между двумя сечениями, не исчезает. Она превращается в тепло, которое в дальнейшем рассеивается. Процесс превращения механической энергии в тепловую и рассеивания последней является необратимым и называется диссипацией. Диссипация характеризуется потерями энергии, приходящимися на единицу длины (гидравлическим уклоном)

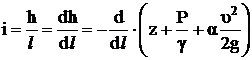. (4)

В соответствии с формулой (4) гидравлический уклон всегда положителен и равен тангенсу угла наклона между касательной и линией энергии в рассматриваемом сечении и отрицательным направлением оси длин.

Изменение потенциальной энергии характеризуется пьезометрическим уклоном

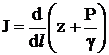. (5)

Для равномерного потока кинетическая энергия по длине не меняется, поэтому в этом случае i = J. При неравномерном движении из-за изменения площади живого сечения потока кинетическая энергия потока изменяется. Соответственно изменяется (увеличивается или уменьшается) потенциальная энергия. В этих условиях пьезометрический уклон может быть и положительным, и отрицательным, и равным нулю.

Уравнение Бернулли широко применяется в различных разделах гидравлики для решения многих практических задач. При помощи уравнения Бернулли выводятся формулы для определения расхода жидкости, проходящей через отверстия, производится гидравлический расчет трубопроводов многих водомерных устройств, выводится основное уравнение неравномерного движения жидкости и т.д.

При переходе жидкости из широко сечения в узкое сечение увеличивается скорость, а давление соответственно уменьшается. Такое сужение на данном приборе называется водомером Вентури и применяется для измерения расхода жидкости в напорном трубопроводе. Для определения расхода измеряют разницу пьезометрических высот h в широком и узком сечениях и по ней судят о величине проходящего расхода.

Зависимость между показаниями пьезометров и расходом жидкости выводится из уравнения Бернулли, написанного для сечения I и II относительно плоскости сравнения, проходящей по оси трубопровода, и уравнением неразрывности

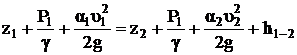, (6)

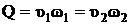, (7)

где z₁ и z₂ – высота центров тяжести живых сечений над произвольно выбранной горизонтальной плоскостью сравнения;

Р₁ и Р₂ – давление в центрах тяжести живых сечений I и II;

υ₁ и υ₂ – средняя скорость движения жидкости в живых сечениях I и II;

h_1-2 – потери напора на участках потока между сечениями I и II;

γ – удельный вес жидкости;

ω₁ и ω₂ – живые сечения потоков на участках I и II.

Учитывая, что z₁ = z₂ (так как плоскость сравнения проходит по оси трубопровода), 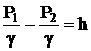(по показанию пьезометра), 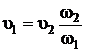(по уравнению неразрывности расхода), уравнение Бернулли может быть написано в виде

, (8)

откуда величина скорости, если принять α₁ = α₂ = 1, а потери напора h_1-2 = 0, приближенно определяется выражением

, (9)

а величина расхода

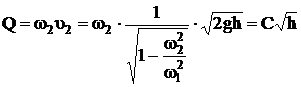. (10)

Величина

,

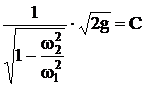зависит от соотношения площадей широкой и узкой частей водомера.

При выводе зависимости мы не учитывали потерь энергии при движении жидкости через прибор; их можно учесть, введя коэффициент расхода водомера m > 1. Тогда окончательная формула для расхода жидкости, проходящей через водомер, получит выражение

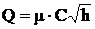. (11)

Коэффициент расхода для новых водомеров m = 0,985 и для водомеров, бывших в употреблении, m = 0,98.

Date: 2015-07-22; view: 1513; Нарушение авторских прав