Система аксиом давида гильберта

АКСИОМАТИЧЕСКИЙ МЕТОД

ПОСТРОЕНИЯ ГЕОМЕТРИИ

ЕВКЛИД

(«Начала», 300 лет до н.э.)

«Определения» базовых понятий:

1. Точка есть то, что не имеет частей. (Σημεῖόν ἐστιν, οὗ μέρος οὐθέν — букв. «Точка есть то, часть чего ничто»)

2. Линия — длина без ширины.

3. Края же линии — точки.

4. Прямая линия есть та, которая равно лежит на всех своих точках.

5. Поверхность есть то, что имеет только длину и ширину.

6. Края же поверхности — линии.

7. Плоская поверхность есть та, которая равно лежит на всех своих линиях.

За определениями Евклид приводит постулаты (I post. 1-5):

1. От всякой точки до всякой точки можно провести прямую.

2. Ограниченную прямую можно непрерывно продолжать по прямой.

3. Из всякого центра всяким раствором может быть описан круг.

4. Все прямые углы равны между собой.

5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.

За постулатами следуют аксиомы (I ax. 1-9), которые имеют характер общих утверждений, относящихся в равной мере как к числам, так и к непрерывным величинам:

1. Равные одному и тому же равны и между собой.

2. И если к равным прибавляются равные, то и целые будут равны.

3. И если от равных отнимаются равные, то остатки будут равны.

4. (И если к неравным прибавляются равные, то целые будут не равны.)

5. (И удвоенные одного и того же равны между собой.)

6. (И половины одного и того же равны между собой.)

7. И совмещающиеся друг с другом равны между собой.

8. И целое больше части.

9. (И две прямые не содержат пространства.)

В скобки взяты аксиомы, принадлежность которых Евклиду Гейберг, автор классической реконструкции текста «Начал», счёл сомнительной. I post. 4 и 5 в ряде списков выступают как I ax. 10 и 11 соответственно.

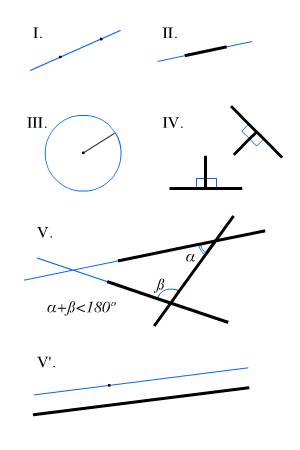
СИСТЕМА АКСИОМ ДАВИДА ГИЛЬБЕРТА

Система аксиом, предложенная в 1899 Д. Гильбертом. Со времени первой публикации. Д. Гильберт внес в систему аксиом различные изменения и уточнения.

Основными (неопределяемыми) понятиями являются объекты: точки, прямые и плоскости и отношения между ними, выражаемые словами: "принадлежит", "между", "конгруэнтен".

Природа основных объектов и отношений между ними может быть какой угодно, лишь бы эти объекты и отношения удовлетворяли указанным аксиомам.

Система содержит 20 аксиом, которые разбиты на пять групп.

I группа состоит из восьми аксиом принадлежности (соединения), которые описывают отношение "принадлежит".

I₁. Для любых двух точек существует прямая, проходящая через каждую из этих двух точек.

I₂. Для двух различных точек существует не более одной прямой, проходящей через каждую из этих двух точек.

I₃. На каждой прямой лежат по крайней мере две точки. Существуют по крайней мере три точки, не лежащие на одной прямой.

I₄. Для любых трех точек, не лежащих на одной прямой, существует плоскость, проходящая через каждую из этих трех точек. На каждой плоскости лежит по крайней мере одна точка.

I₅. Для любых трех точек, не лежащих на одной прямой, существует не более одной плоскости, проходящей через каждую из этих трех точек.

I₆. Если две точки А,В прямой a лежат в плоскости , то всякая точка прямой a лежит в плоскости .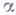

I₇. Если две плоскости имеют общую точку, то они имеют еще по крайней мере одну общую точку.

I₈. Существуют по крайней мере четыре точки, не лежащие в одной плоскости.

II группа содержит четыре аксиомы порядка, описывающие отношение "между".

II₁. Если точка В лежит между точкой А и точкой С, то А, В, С - различные точки одной прямой и В лежит также между Си А.

II₂. Для любых двух точек А и В на прямой АВ существует по крайней мере одна точка С такая, что точка В лежит между А и С.

II₃. Среди любых трех точек прямой существует не более одной точки, лежащей между двумя другими.

II₄ (аксиома Паша). Пусть А, В, С - три точки, не лежащие на одной прямой, и а - прямая в плоскости ABC, не проходящая ни через одну из точек А, В, С. Тогда, если прямая а проходит через внутреннюю точку отрезка АВ, то она проходит также через внутреннюю точку отрезка АС или через внутреннюю точку отрезка ВС.

III группа содержит пять аксиом конгруэнтности, которые описывают отношение "конгруэнтен" (это отношение Гильберт обозначает знаком ).

III₁. Если даны отрезок АВ и луч ОХ, то на луче ОX существует точка В' такая, что отрезок АВ конгруэнтен отрезку ОВ', то есть .

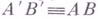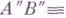
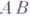III₂. Если и , то .

III₃,. Пусть АВ и ВС- два отрезка на прямой, не имеющие общих внутренних точек, а 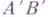и 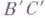- два отрезка на той же или на другой прямой, тоже не имеющие общих внутренних точек. Тогда, если и , то

III₄. Пусть даны угол АОВ, луч О'А' и полуплоскость П', ограниченная прямой О'А'. Тогда в полуплоскости П' существует один и только один луч О'В' такой, что . Кроме того, каждый угол конгруэнтен самому себе.

III₅. Если для двух треугольников ABC и А'В'С' имеем: 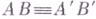, , 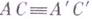, то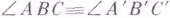

IV группа состоит из двух аксиом непрерывности.

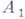IV₁ (аксиома Архимеда). Пусть АВ и CD -два каких-нибудь отрезка. Тогда на прямой АВ существует конечное множество точек таких, что точка лежит между 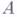и 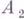, точка 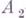лежит между 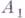и 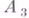и т. д., причем отрезки 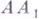, , 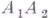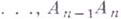конгруэнтны отрезку CD и В лежит между A и An.

IV2 (аксиома Кантора). Пусть на какой-либо прямой а задана бесконечная последовательность отрезков 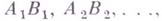удовлетворяющая двум условиям:

а) каждый последующий отрезок есть часть предыдущего,

б) для любого наперед заданного отрезка CD найдется натуральное число n такое, что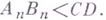

Тогда на прямой а найдется точка М, принадлежащая каждому из отрезков этой последовательности.

V группа содержит одну аксиому о параллельных.

Пусть даны прямая а и точка А, не лежащая на этой прямой. Тогда в плоскости, определяемой прямой а и точкой А, существует не более одной прямой, проходящей через точку А и не пересекающей прямую а.

Все остальные понятия евклидовой геометрии определяются с помощью основных понятий, а все предложения о свойствах геометрических фигур могут (должны) быть доказаны чисто логическим выводом из этих аксиом (или предложений, полученных таким же путем).