Задание 6

1. Товаровед проверяет изделия на стандартность, но проверяет не более пяти изделий. Составить закон распределения числа проверенных изделий, если вероятность того, что изделие будет признано стандартным, равна 0,6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.

2. В лотерее на 1000 билетов разыгрываются три вещи, стоимости которых 50, 30 и 20 рублей. Составить закон распределения суммы выигрыша для лица, имеющего два билета. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.

3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе пять библиотек. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.

4. Вероятность того, что вошедший в магазин покупатель сделает покупку, равна 0,4. Предполагая, что покупатель делает не более одной покупки, составить закон распределения числа покупок, сделанных в магазине, если вошло 5 человек. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, полученной случайной величины.

5. Имеются 4 ключа из которых только один подходит к замку. Составить закон распределения числа попыток открывания замка, если испробованный ключ в после­дующих попытках не участвует. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

6. В магазине имеются 20 телевизоров, из них 7 имеют дефекты. Необходимо: а) составить закон распределения числа телевизоров с дефектами среди выбранных наудачу пяти; б) найти математическое ожидание и дисперсию этой случайной величины: в) определить вероятность того, что среди выбранных нет телевизоров с дефектами.

7. Распределение дискретной случайной величины задано формулой p{ =k} =Ck², где k =1, 2, 3, 4, 5. Найти: а) константу С; б) вероятность события | –2| £ 1.

8. Дискретная случайная величина – число мальчиков в семьях с 4 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения ; б) найдите вероятности событий: А – в семье не менее 2, но не более 3 мальчиков; В – не более 3 мальчиков; С – более одного мальчика. Найти среднее квадратическое отклонение случайной величины .

9. C вероятностью попадания при одном выстреле 0,8 охотник стреляет по дичи до первого попадания, но успевает сделать не более 3 выстрелов. Дискретная случайная величина – число промахов. а) Найдите закон распределения . б) Найдите вероятности событий: <2; £2; 1 < £ 3. в) Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s [ ].

10. 2 стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого стрелка при одном выстреле – 0,6, для второго – 0,7. Дискретная случайная величина – число попаданий в мишень. а) Найдите закон распределения . б) Найдите вероятность события ³ 1.в) Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

11. В коробке имеется 8 карандашей, из которых 3 красных. Из этой коробки наудачу извлекаются 3 карандаша. а) Найдите закон распределения случайной величины , равной числу красных карандашей в выборке. б) Найдите вероятность события 0< £2. в) Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

12. Автомат штампует детали. Контролируется длина детали , которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактическая длина изготовленных деталей не менее 48 мм и не более 52 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 49 мм; б) меньше 51 мм. (Указание: из равенства Р (48< <52) = 1 предварительно найти s).

13. В партии из 10 деталей имеется 5 стандартных. Из этой партии наудачу взято 3 детали. Найдите закон распределения случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

14. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка – 0,5, для второго – 0,6. Найдите закон распределения случайной величины , равной общему числу попаданий в мишень. Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

15. Рабочий обслуживает 3 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка – 0,7, для второго – 0,8, для третьего – 0,9. Найдите закон распределения случайной величины , равной числу станков, которые не потребуют внимания рабочего. Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

16. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x) =1/16(x²–4x+4). Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

17. Случайная величина , сосредоточенная на интервале [–1,3], задана функцией распределения F(x)=0,25x+0,25. Найти вероятность попадания случайной величины в интервал [0; 2]. Построить график функции F(x).

18. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x²–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

19. Вероятность попадания стрелком при каждом выстреле равна 0,4. Имея в запасе 6 патронов, он ведет стрельбу до первого попадания в мишень или до израсходования всех патронов. Найдите закон распределения случайной величины , равной числу израсходованных патронов. Найти математическое ожидание М[ ], дисперсию D[ ], среднее квадратическое отклонение s[ ].

20. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x²–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.

21. Торговый агент имеет 5 телефонных номеров потенциальных покупателей и звонит им до тех пор, пока не получит заказ на покупку товара. Вероятность того, что потенциальный покупатель сделает заказ, равна 0,4. Составить закон распределения числа телефонных разговоров, которые предстоит провести агенту. Найти математическое ожидание и дисперсию этой случайной величины.

22. Стрелок ведет стрельбу по цели с вероятностью попа­дания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

23. Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или до израсходования всех патронов. Вероятность попадания при первом выстреле равна 0,6, при каждом последующем – уменьшается на 0,1. Необходимо: а) составить закон распределения числа патронов, израсходованных охотником; б) найти математическое ожидание и дисперсию этой случайной величины.

24. Экзаменатор задает студенту вопросы, пока тот правильно отвечает. Как только число правильных ответов достигнет четырех либо студент ответит неправильно, экзаменатор прекращает задавать вопросы. Вероятность правильного ответа на один вопрос равна 2/3. Составить закон распределения числа заданных студенту вопросов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

25. Каждый поступающий в институт должен сдать 3 экза­мена. Вероятность успешной сдачи первого экзамена 0,9, второго – 0,8, третьего – 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти математическое ожидание и дисперсию этой случайной величины.

26. По данным длительной проверки качества запчастей определенного вида брак составляет 3%. Изготовлено 1000 запчастей. Определить математическое ожидание и среднее квадратическое отклонение числа годных запчастей.

27. Найти вероятность того, что в течение смены произойдет не более двух отказов оборудования, при условии, что среднее число отказов в течение смены равно 1,6. (Предполагается, что число отказов имеет распределение Пуассона.)

28. Вероятность сдачи первого экзамена для данного студента равна 0.7, второго экзамена – 0.8, третьего – 0.7. С.в. – число сданных экзаменов. Найти ряд распределения и математическое ожидание с.в. . Вычислить значение функции распределения с.в. в точках 0; 1; 2,5; 10.

29. Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,9. В контрольной партии четыре прибора. С.в. – число приборов, удовлетворяющих требованиям качества. Найти ряд распределения и математическое ожидание с.в. . Вычислить значение функции распределения с.в. X в точках 0; 1; 2,5; 10.

30. Функция распределения случайной величины имеет вид:

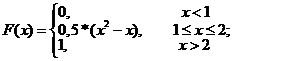
Найти функцию плотности распределения с.в. и построить ее график. Найти медиану с.в. . Вычислить значение функции распределения с.в. в точках 0; 1; 2,5; 10. Найти вероятность попадания значения с.в. в интервал (1.2, 1,5).

Date: 2015-07-23; view: 2242; Нарушение авторских прав