Методичний інструментарій оцінки вартості грошей у часі. а)оцінкамайбутньої вартості грошей за простимивідсотками:

а)оцінкамайбутньої вартості грошей за простимивідсотками:

FV = PV·(1+n·i),

де PV – початкова сума вкладу;

п – загальний строк вкладу, роки;

і – проста відсоткова річна ставка, в долях одиниці.

б) оцінкавартості грошей за складнимивідсотками:

- при нарахуваннівідсотків 1 раз на рік:

FV = PV·(1+j)ⁿ,

де j – ставка складного відсотка, в долях одиниці;

п – тривалість нарахування відсотків, років,

-при частішому, ніж 1 раз на рік, нарахуванні відсотків:

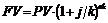
де k – кількість інтервалів нарахування відсотків у році.

в) сума нарахованих відсотків:

I = FV – PV,

г) ефективнапроцентнаставка в процесінарощеннявартостікоштів за складнимивідсотками:

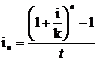
де i – річнапроцентна ставка при складному нарахуванні відсотків,в долях одиниці;

k – кількість інтервалів нарахування відсотків у календарному році;

n – число раз нарахування відсотків протягом усього терміну дії депозитної угоди;

t – кількість років дії депозитної угоди.

Характеризує ставку простого відсотку, яка дозволяє отримати такий саме дохід, як і ставка складного відсотку (і).

д) оцінка вартості грошей при ануїтеті:

- майбутня вартість ануїтету за умови попередніх або авансових платежів (пренумерандо):

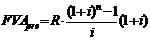
- майбутня вартість ануїтету за умови наступних платежів (постнумерандо):

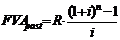
де R – сума періодичного платежу (ануїтет);

i – періодична ставка (річна, місячна або квартальна), в долях одиниці;

n – число раз нарахування відсотків протягом усього періоду.

е) прогнозування річного темпу інфляції:

ТІр = (1+ТІм)¹² –1

де ТІм – місячний темп інфляції, в долях одиниці;

ж) реальна процентна ставка з урахуванням фактору інфляції (модель Фішера):

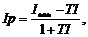
де I_ном – річна номінальна процентна ставка, в долях одиниці;

ТІр – річний темп інфляції, в долях одиниці.

Приклад 1.

Інвестор планує розмістити 100 тис. грн. на депозитний рахунок під 16% річних строком на 2 роки. Перший банк пропонує йому щоквартальне нарахування простих відсотків, другий – нарахування складних відсотків в кінці кожного року, третій – щоквартальне нарахування складних відсотків, четвертий щомісячне нарахування складних відсотків. Обґрунтувати вибір інвестора за допомогою розрахунку ефективної процентної ставки. Розрахувати можливий дохід інвестора за кожним варіантом.

Розв’язання:

1) Розрахунок ефективної процентної ставки:

- 1 й банк: і_е1 = 16%, оскільки при простому нарахуванні відсотків кінцева сума від частоти нарахування не залежить;

- 2-й банк:

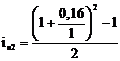=0,173 (17,3%)

- 3-й банк:

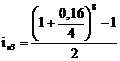=0,184 (18,4%)

- 4-й банк:

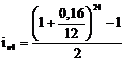=0,187 (18,7%)

Інвестор обере четвертий варіант.

2) Розрахунок можливого доходу інвестора:

- за першим варіантом:

FV₁ = 100·(1+2·0,16) = 132 тис.грн.,

оскільки при простому нарахуванні відсотків кінцева сума від частоти нарахування не залежить.

I₁ = FV – PV = 132 – 100 = 32 тис.грн.;

- за другим варіантом:

FV₂ = 100·(1+ 0,16)² = 134,6 тис.грн.;

I₂ = 134,6 – 100 = 34,6 тис.грн.;

- за третім варіантом:

FV₃ = 100·(1+ 0,16/4)^2×4 = 136,9 тис.грн.;

I₃ = 136,9 – 100 = 36,9 тис.грн.;

- за четвертим варіантом:

FV₄ = 100·(1+ 0,16/12)^2×12 = 137,4 тис.грн.;

I₄ = 137,4 – 100 = 37,4 тис.грн.

Найбільший дохід інвестор отримає за умовами четвертого банку.

Приклад 2.

Щомісяця частина заробітної плати фізичної особи в сумі 2000 грн. перераховується на депозитний накопичувальний рахунок. Розрахувати дохід вкладника через 3 роки від розміщення коштів на накопичувальному рахунку під 15% річних з щомісячним нарахуванням складних відсотків. Застосувати методи пренумерандо і постнумерандо.

Розв’язання:

Дохід вкладника, розрахований за методом пренумерандо:

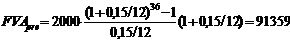грн.

у тому числі відсотковий дохід:

I_pre = 91359 – (2000×36) = 91359 – 72000 = 19359 грн.

Дохід вкладника, розрахований за методом постнумерандо:

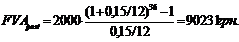
у тому числі відсотковий дохід:

I_post = 90231 – (2000×36) = 18231 грн.

Приклад 3.

Розрахувати реальну річну процентну ставку за депозитом з урахуванням інфляції, якщо номінальна дохідність депозиту становить 17% річних, а річний темп інфляції 12%. Розрахувати номінальний і реальний дохід вкладника від розміщення на депозит 50 тис.грн. на 9 місяців з щомісячним нарахуванням складних відсотків. Визначити втрати вкладника від інфляції.

Розв’язання:

Реальна процентна ставка з урахуванням інфляції:

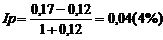
Номінальний сукупний дохід вкладника:

FV_Н = 50·(1+ 0,17/12)⁹ = 56,7 тис.грн.

у тому числі нараховані відсотки:

I_Н = 56,7 –50 = 6,7 тис.грн.

Реальний сукупний дохід вкладника:

FV_Р = 50·(1+ 0,04/12)⁹ = 51,5 тис.грн.

у тому числі нараховані відсотки:

I_Р = 51,5 –50 = 1,5 тис.грн.

Втрати від інфляції:

FV_Н – FV_Р = 56,7 – 51,5 = 5,2 тис.грн. або

І_Н – І_Р = 6,7 – 1,5 = 5,2 тис.грн.

Date: 2015-07-23; view: 370; Нарушение авторских прав