
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интегральная формула Коши
|
|
Основные понятия
1. Понятие интеграла от функции комплексного переменного вводится (так же, как и в действительной области) как предел последовательности интегральных сумм; функция при этом определена на некоторой кривой  , кривая предполагается гладкой или кусочно-гладкой:
, кривая предполагается гладкой или кусочно-гладкой:

где 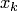 — точка, выбранная на дуге
— точка, выбранная на дуге 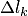 разбиения кривой;
разбиения кривой; 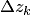 — приращение аргумента функции на этом участке разбиения,
— приращение аргумента функции на этом участке разбиения, 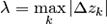 — шаг разбиения,
— шаг разбиения, 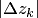 — длина хорды, соединяющей концы дуги
— длина хорды, соединяющей концы дуги 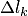 ; кривая
; кривая  разбивается произвольным образом на
разбивается произвольным образом на 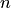 частей
частей 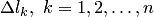 . На кривой выбрано направление, т.е. указаны начальная и конечная точки. В случае замкнутой кривой
. На кривой выбрано направление, т.е. указаны начальная и конечная точки. В случае замкнутой кривой 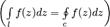 интегрирование происходит в положительном направлении, т.е. в направлении, оставляющем слева конечную область, ограниченную контуром.
интегрирование происходит в положительном направлении, т.е. в направлении, оставляющем слева конечную область, ограниченную контуром.
Формула (2.43) определяет криволинейный интеграл от функции комплексного переменного. Если выделить действительную и мнимую части функции 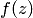 , т.е. записать ее в виде
, т.е. записать ее в виде
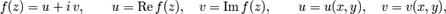
то интегральную сумму можно записать в виде двух слагаемых, которые будут являться интегральными суммами криволинейных интегралов второго рода от функций двух действительных переменных. Если 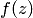 предположить непрерывной на
предположить непрерывной на  , то
, то 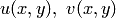 будут также непрерывны на
будут также непрерывны на  , и, следовательно, будут существовать пределы соответствующих интегральных сумм. Поэтому, если функция
, и, следовательно, будут существовать пределы соответствующих интегральных сумм. Поэтому, если функция 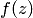 непрерывна на
непрерывна на  , то предел в равенстве (2.43) существует, т.е. существует криволинейный интеграл от функции
, то предел в равенстве (2.43) существует, т.е. существует криволинейный интеграл от функции 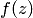 по кривой
по кривой  и имеет место формула
и имеет место формула
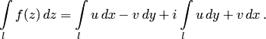
Интеграл от функции со степенной особенностью. Разрезы на комплексной плоскости.
Иногда подынтегральная функция такова, что выбор контура осложняется сильной ограниченностью вариантов элементов контура, по которым
интеграл удастся вычислить. На примере интеграла  поясним суть проблемы и укажем, как поступать в этом случае.
поясним суть проблемы и укажем, как поступать в этом случае.
Вычислять будем контурный интеграл 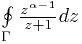 . Выберем контур интегрирования. Естественно, в него войдёт полуось
. Выберем контур интегрирования. Естественно, в него войдёт полуось 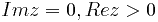 .
.
Только точку 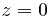 нужно обойти: степенная функция многозначна, а точка
нужно обойти: степенная функция многозначна, а точка 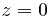 является точкой ветвления.
является точкой ветвления.
Как можно замкнуть контур? Оказывается, оптимальный вариант - контур, изображённый на рис. 9.
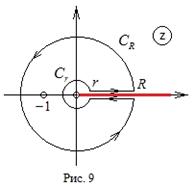
Поясним рис. 9. Подынтегральная функция многозначна, так как в ней присутствует степенная функция.
Вообще говоря, логарифмическая функция в предыдущих примерах тоже была многозначна, но к каким-то специфическим следствиям это
не приводило. Отличие в выбранном контуре. В данном примере при обходе контура мы обходим точку ветвления, вследствие чего может
произойти переход к другой ветви многозначной функции. Чтобы этого избежать, вводится разрез (отмечен красной прямой).
В результате когда мы проходим отрезок 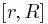 слева направо, мы двигаемся по верхнему берегу разреза. Когда мы обошли точку
слева направо, мы двигаемся по верхнему берегу разреза. Когда мы обошли точку
ветвления по участку 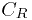 и двигаемся по тому же отрезку, но в обратном направлении, то мы уже двигаемся по нижнему берегу разреза.
и двигаемся по тому же отрезку, но в обратном направлении, то мы уже двигаемся по нижнему берегу разреза.
Формально это означает, что необходимо учитывать увеличение аргумента на 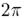 при обходе точки ветвления.
при обходе точки ветвления.
Переходим к вычислению. Сразу заметим, что интегралы по дугам окружностей в пределе  и
и  стремятся к нулю - это легко показать.
стремятся к нулю - это легко показать.
Аккуратно проведём интегрирование по берегам разреза:
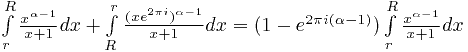 .
.
В пределе  и
и  получим с точностью до множителя искомый интеграл.
получим с точностью до множителя искомый интеграл.
С другой стороны внутри контура интегрирования попал простой полюс подынтегральной функции  , причём
, причём
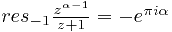 .
.
Таким образом,
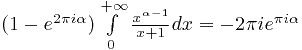 ,
,
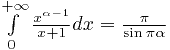 .
.
Следствие 1 (теорема Коши для составного контура).
Пусть G – многосвязная область с внешним контуром 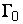 и внутренними контурами
и внутренними контурами  Если функция f(z) – аналитическая в области и на ее границе, то справедливо равенство:
Если функция f(z) – аналитическая в области и на ее границе, то справедливо равенство:
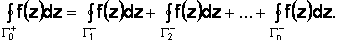 (1.53)
(1.53)
Здесь внешний контур обходится в положительном направлении, т. е. против часовой стрелки, а внутренние контуры обходятся в отрицательном направлении, т. е. по часовой стрелке.
Интегральная формула Коши
В следующей теореме, в отличие от двух предыдущих, рассматривается интеграл от функции, которая, не являясь аналитической в области, ограниченной контуром интегрирования, имеет специальный вид.
Теорема 2.3. Если функция 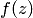 является аналитической в области
является аналитической в области 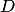 и на ее границе
и на ее границе 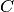 , то для любой внутренней точки
, то для любой внутренней точки  области
области 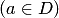 имеет место равенство
имеет место равенство
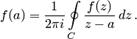
| (2.57) |
Область 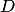 может быть односвязной или многосвязной, а граница области -простым или сложным контуром.
может быть односвязной или многосвязной, а граница области -простым или сложным контуром.
Доказательство для случая односвязной области опирается на результат теоремы 2.1, а для многосвязной — приводится к случаю односвязных областей (как при доказательстве теоремы 2.2) путем проведения разрезов, не проходящих через точку  .
.
Следует обратить внимание на то, что точка а не принадлежит границе области и поэтому подынтегральная функция является непрерывной на 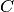 и интеграл существует.
и интеграл существует.
Теорема представляет собой важный прикладной интерес, а именно по формуле (2.57) решается так называемая краевая задача теории функций: по значениям функции на границе области определяется ее значение в любой внутренней точке.
Замечание 2.11. В условиях теоремы интеграл 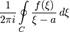 определяет аналитическую функцию в любой точке
определяет аналитическую функцию в любой точке  , не принадлежащей контуру
, не принадлежащей контуру 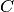 , причем в точках конечной области
, причем в точках конечной области 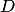 , ограниченной контуром, он равен
, ограниченной контуром, он равен 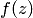 (по формуле (2.57)), а вне
(по формуле (2.57)), а вне 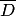 — равен нулю в силу оснований теоремы Коши. Этот интеграл, называемый интегралом Коши, является частным случаем интеграла типа Коши (2.48). Здесь контур замкнутый, в отличие от произвольного в (2.48), а функция
— равен нулю в силу оснований теоремы Коши. Этот интеграл, называемый интегралом Коши, является частным случаем интеграла типа Коши (2.48). Здесь контур замкнутый, в отличие от произвольного в (2.48), а функция 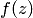 является аналитической, в отличие от непрерывной на
является аналитической, в отличие от непрерывной на  в (2.48). Для интеграла Коши, следовательно, справедливо сформулированное для интеграла типа Коши утверждение 2.26 о существовании производных. Можно сформулировать на основании этого следующее утверждение.
в (2.48). Для интеграла Коши, следовательно, справедливо сформулированное для интеграла типа Коши утверждение 2.26 о существовании производных. Можно сформулировать на основании этого следующее утверждение.
| <== предыдущая | | | следующая ==> |
| Послесловие. «Самое большое открытие человека – это сила, умение омолодить себя физически, умственно и духовно рациональным голоданием» | | | Египетские пирамиды |
Date: 2015-07-22; view: 1000; Нарушение авторских прав