Теоретическое введение. 1 Ознакомиться с экспериментальным подтверждением квантовых свойств атома в опытах Франка и Герца

Лабораторная работа № 69

ОПРЕДЕЛЕНИЕ РЕЗОНАНСНОГО ПОТЕНЦИАЛА

МЕТОДОМ ФРАНКА И ГЕРЦА

Цель работы

1 Ознакомиться с экспериментальным подтверждением квантовых свойств атома в опытах Франка и Герца

2 Изучить процесс возбуждения атомов инертного газа электронами.

3 Измерить первый потенциал возбуждения («резонансный потенциал»).

4 Определить тип газа по значению первого потенциала возбуждения («резонансного потенциала»).

Теоретическое введение

В начале XX века в физике был выполнен ряд исследований, которые легли в основу квантовой механики и атомной теории. В 1900 г. Макс Планк, рассматривая задачу о равновесном излучении черного тела, ввел (чуждую классической физике) гипотезу о том, что излучение света веществом происходит не непрерывно, а отдельными порциями, или «квантами».

Развивая идеи Планка, в 1905 г. Альберт Эйнштейн предположил, что дискретность присуща не только процессу излучения, но и процессу поглощения излучения веществом.

Наконец, в 1913 г. Нильс Бор применил принцип дискретности энергии к любым атомным системам. Теория Бора стала важным шагом на пути к пониманию внутриатомных явлений. Однако первоначально она встретила скептическое отношение физического сообщества. Причиной тому была двойственность теории: применяя законы классической механики для описания движения электрона в атоме, она дополняла их противоречащими классической электродинамике принципами. Поэтому теория Бора нуждалась в поддержке экспериментальными результатами.

Важным подтверждением справедливости теории стали данные, полученные в области физики электрон-атомных столкновений в результате серии экспериментов, поведенных в 1912-1914 гг. Джеймсом Франком и Густавом Герцем. Значение экспериментов оказалось столь большим, что вскоре после общественного признания теории Бора (Нобелевская премия по физике, 1922) Нобелевскую премию в 1925 г. получили и авторы опытов - как отмечалось в официальном сообщении Нобелевского комитета, «за прямое экспериментальное подтверждение существования дискретных энергетических уровней электрона в атоме».

Важное следствие из принципа дискретности энергетических состояний электрона атоме по теории Бора состоит в том, что передача энергии электронам атома в любом процессе должна происходить также дискретными порциями (квантами), а возможная величина этих квантов должна, по правилу частот Бора, соответствовать атомным спектрам.

Одним из возможных механизмов передачи энергии атому является неупругое взаимодействие с ним свободного электрона, или неупругое рассеяние электрона на атоме. Вследствие большой разницы в массах электрона и атома, лишь очень малая часть кинетической энергии соударяющегося электрона, переходит в кинетическую энергию атома:

Δ T ~ (m/M)·T, (1)

где Δ T – изменение кинетической энергии электрона после столкновения,

T - кинетическая энергия электрона до столкновения, m - масса электрона,

M - масса атома.

Поэтому в процессе неупругого столкновения почти все изменение кинетической энергии электрона связано с изменением внутренней энергии атома (если не происходит ионизация атома).

Опыты Франка-Герца подтверждают эти рассуждения, а именно показывают:

- при скоростях электронов, меньших некоторой критической скорости, соударение происходит упруго, т.е. электрон не передаёт атому своей энергии, а отскакивает от него, изменяя лишь направление своей скорости;

- при скоростях, достигающих критической скорости, соударение происходит неупруго, т.е. электрон теряет свою энергию, передавая её атому, который при этом переходит в другое стационарное состояние, характеризуемое большей энергией;

- энергия, передаваемая электроном атому, всегда имеет дискретные значения.

Таким образом, атом или вообще не воспринимает энергию (упругий удар), а если воспринимает её, то только в количествах, равных разности энергий в двух стационарных состояниях.

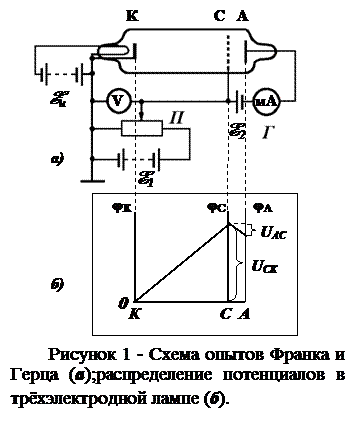
Основным элементом экспериментальной установки Франка и Герца (рисунок 1 а) является трехэлектродная лампа (триод), заполненная парами ртути при низком давлении (порядка 1 мм. рт. ст.). Нить накала, питаемая током от источника ЭДС E_н, нагревает катод К, обеспечивая тем самым эмиссию электронов с его поверхности. В отличие от стандартного включения триода (когда сетка имеет отрицательный потенциал относительно катода и управляет потоком электронов к аноду), в опыте Франка и Герца сетка С имеет положительный потенциал φ _С относительно катода К и играет роль ускоряющего электрода. Этот потенциал создаётся и регулируется с помощью потенциометра П, подключённого к источнику ЭДС E_1. Напряжение сетка - катод U _СК = φ_С - φ_К измеряется с помощью вольтметра V. Поскольку потенциал катода принимается равным нулю (φ_К = 0), в дальнейшем будем говорить о потенциале сетки φ _С вместо “напряжение сетка - катод U _СК ”

Между сеткой С и анодом (коллектором) А с помощью источника ЭДС E₂ ≈ 0,5 В создаётся слабое тормозящее поле. Распределение потенциалов между электродами лампы представлено на рисунке 1 б. Электроны, вылетающие из катода, на участке сетка - катод ускоряются, приобретая энергию W_к = е φ_С, где е - заряд электрона.

Часть электронов, пролетающих через сетку и способных преодолеть тормозящее поле анод - сетка, попадает на коллектор, обуславливая некоторый ток I, который измеряется гальванометром Г.

Двигаясь от катода к сетке, электроны сталкиваются с атомами ртути, находящимися в основном энергетическом состоянии. Характер столкновений электрона с атомом будет существенно зависеть от значения кинетической энергии электрона W_{к .} Если W_К < Δ Е (где Δ Е = E ₁ - E ₀ разность энергий между основным E ₀ и первым возбужденным E ₁ состояниями атома), то соударение электрона с атомом в этом случае будет упругим. В таком столкновении кинетическая энергия электрона не переходит во внутреннюю энергию атома, и в силу большого различия масс соударяющихся частиц, электрон будет двигаться в газовом промежутке между катодом и сеткой практически без потерь энергии. Такие электроны, пролетев сетку лампы, легко преодолеют слабое тормозящее поле между сеткой и анодом и обеспечат протекание тока в цепи анода. В этом случае при увеличении потенциала сетки φ _С ток в цепи анода будет монотонно возрастать.

Однако если при движении в ускоряющем поле электрон приобретет кинетическую энергию, достаточную для возбуждения атома (W_К = Δ Е), то соударение такого электрона с атомом станет неупругим. При этом значительная часть кинетической энергии электрона будет переходить во внутреннюю энергию атома, то есть расходоваться на возбуждение атома. Максимальную кинетическую энергию электроны приобретают, подлетая к сетке, поэтому их неупругие столкновения с атомами начинают происходить вблизи сетки. После столкновений энергетически «ослабленные» электроны уже не смогут преодолеть тормозящее поле промежутка анод-сетка и попасть на анод. Следовательно, когда ускоряющий потенциал сетки достигнет значения φ ₁ = Δ Е/e, ток I в цепи коллектора должен резко уменьшиться. Значение ускоряющего потенциала φ ₁ называется резонансным потенциалом возбуждения атома (термин введён Франком и Герцем). Измеряя экспериментально резонансный потенциал атома, можно найти энергию Δ Е перехода атома в возбужденное состояние.

При дальнейшем увеличении ускоряющего потенциала φ _С ток, регистрируемый гальванометром, будет снова возрастать. Однако, когда значение ускоряющего потенциала станет равным φ ₂ = 2 φ ₁, ток в цепи коллектора снова резко уменьшится, так как в этих условиях электрон при пролете газового промежутка может дважды испытать неупругие столкновения с атомами. Соответственно, возможны режимы с тремя неупругими столкновениями при φ ₃ = 3 φ ₁ и т.д.

Итак, если имеет место квантование энергии электрона в атоме, то при значениях ускоряющего потенциала φ _С на сетке, кратных φ ₁, на кривой зависимости тока I в цепи коллектора от ускоряющего напряжения U на сетке должны наблюдаться резко выраженные спады. При этом расстояние Δ U между началами этих спадов по шкале ускоряющего напряжения связано с энергией возбуждения Δ E атома соотношением Δ E = e Δ U ₁.

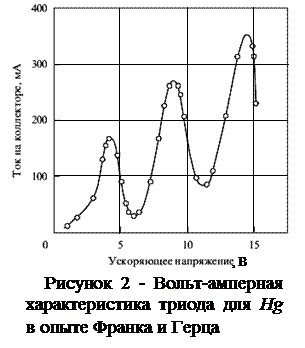Зависимость I (U), полученная в опытах Франка и Герца для паров ртути (рисунок 2), прекрасно подтвердила этот вывод. Такая зависимость является убедительным экспериментальным доказательством дискретности энергетических состояний электронов в атоме.

В частности, из представленного на рисунке 2 графика следует, что первое возбужденное состояние атома ртути отделено от основного состояния энергетическим промежутком в 4,9 эВ.

Принципиально важно, что данные эксперименты могут быть проведены только с одноатомными газами или парами металлов. Если электрон сталкивается с молекулой, становится возможной передача энергии в колебательное и вращательное движения молекулы, кванты которых значительно меньше квантов электронного возбуждения. В этом случае для наблюдения уменьшения энергии электронов требуются гораздо более тонкие методы. Поэтому для опытов Франка-Герца обычно используют пары металлов (ртуть, щелочные металлы) и инертные газы (гелий, неон и др.).

Другой важный результат опыта Франка и Герца с атомами ртути связан с излучением лампой ультрафиолетового света, которое начинается, как только разность потенциалов между катодом и сеткой достигает значения 4,9 В. Это излучение можно наблюдать (например, с помощью люминесцентного экрана в затемнённом помещении), если колбу лампы изготовить из кварца или стекла, пропускающего ультрафиолетовое излучение.

Такое излучение объясняется тем, что возбужденные электронными ударами атомы ртути возвращаются в основное состояние, испуская избыточную энергию в виде квантов излучения. Длина волны такого излучения с энергией фотона ε = Δ E = 4,9 эВ = 7,84∙10^-19 Дж равна

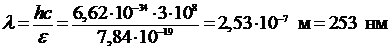(2)

И такая линия действительно была найдена Франком и Герцем.

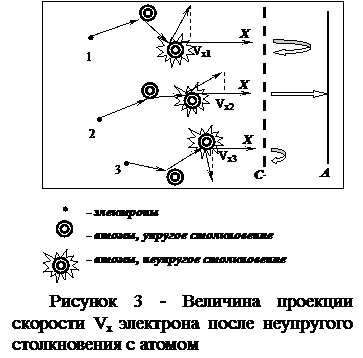
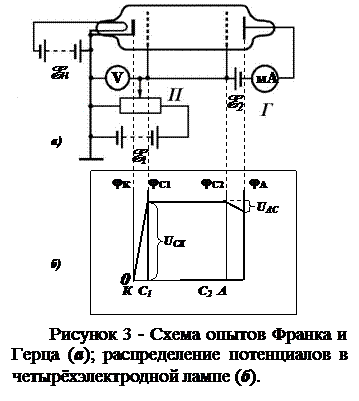В последующих опытах Франк и Герц видоизменили конструкцию лампы таким образом, что накопление энергии электроном происходило в одной части прибора, а столкновения - в другой. С этой целью они ввели в прибор дополнительную сетку, расположенную от нити накала на расстоянии, малом по сравнению со средней длиной свободного пробега электрона (рисунок 3 а). Электроны, получившие всю свою энергию в промежутке катод – сетка 1, попадают в свободное от поля пространство между сеткой 1 и сеткой 2 (φ_{С 1} = φ_{С 2}) и там испытывают многочисленные соударения с атомами газа (рисунок 3 б). При выходе электронов из этого пространства те из них, которые потеряли свою энергию, тормозятся полем анод - сетка 2, и повторяется описанный выше процесс. При помощи этого метода оказалось возможным разделять максимумы, отстоящие друг от друга на доли вольта, и обнаруживать слабо выраженные максимумы. Подавая на сетки потенциал, кратный резонансному, можно наблюдать на вольт-амперной характеристике серию пиков, аналогичных рисунку 2.

В этих опытах были найдены дискретные значения энергии, поглощаемой (и излучаемой) атомами гелия, а также паров калия, натрия. Таким образом, постулаты Бора получили неоспоримое экспериментальное подтверждение.

Значения потенциалов возбуждения (резонансных потенциалов) для различных элементов приведены в таблице 1.

Таблица 1 - Значения потенциалов возбуждения

Несколько причин приводят к тому, что провалы экспериментальной зависимости I (U) не являются идеально резкими, и происходит некоторый сдвиг максимумов на кривой в сторону меньших энергий:

1 Существенный разброс энергии электронов из-за наличия области пространственного заряда в прикатодной области и высокой температуры термоэмиссионного катода (для данного случая справедлива максвелловская функция распределение частиц по скоростям и энергиям);

2 Падение напряжения на катоде прямого накала при протекании по нему тока накала, приводящее к различным значениям потенциала для разных точек катода;

3 Зависимость сечения возбуждения атомов ртути либо инертного газа от энергии электрона;

4 Разброс продольной составляющей скорости электронов после неупругого столкновения, величина которой определяет возможность преодоления задерживающего поля анод-сетка (рисунок 3).

Следует также отметить, что напряжение катод-сетка U _кс, измеренное вольтметром, отличается от истинного значения. Это объясняется тем, что катод и сетка изготовлены из различных металлов. Различные металлы при одинаковых внешних условиях отличаются друг от друга концентрацией свободных электронов и работой выхода электронов из металла. При соединении этих металлов происходит переход свободных электронов из металла с большей концентрацией электронов в металл, содержащий меньшую концентрацию электронов. В результате между металлами возникает контактная разность потенциалов U _конт. Истинное значение напряжения между катодом и сеткой U равно алгебраической сумме U _кс и U _конт.

Чтобы избежать погрешности, обусловленной наличием контактной разности потенциалов U _конт, при определении потенциала возбуждения следует рассматривать разность потенциалов между двумя максимумами вольт-амперной характеристики.

Эксперимент Франка-Герца можно сделать более наглядным, если применить осциллографический метод снятия вольт-амперной характеристики (рисунок 4). В этом случае на участок сетка-катод триода 1 от блока управления 2 подаётся пилообразное напряжение некоторой частоты. Это же напряжение подается на вход 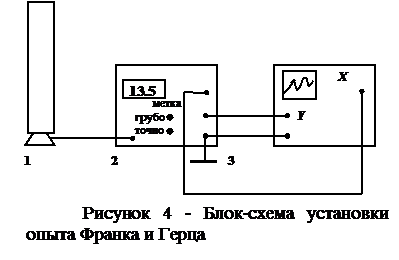Х осциллографа 3, создавая развёртку луча на экране. На вход У осциллографа подаётся напряжение, пропорциональное анодному току триода. Тогда зависимость У (Х) в определенном масштабе представляет собой искомую функциональную связь I = f (U). Масштабы изображения по осям Х и У можно легко изменять, пользуясь соответствующими регулировками усиления осциллографа. В результате на экране наблюдается вольт-амперная характеристика триода, повторяющая форму рисунка 2.