
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Момент силы. 1). Момент силы относительно точки
|
|
1). Момент силы относительно точки.
Рассмотрим материальную точку с массой m, которая может вращаться относительно некоторой точки О под действием приложенной силы F.
Для простоты и наглядности чертежа поместим начало координат в точку О, материальная точка с массой m пусть находится. в плоскости ХОУ, а сила Fнаправлена вдоль оси ОХ.
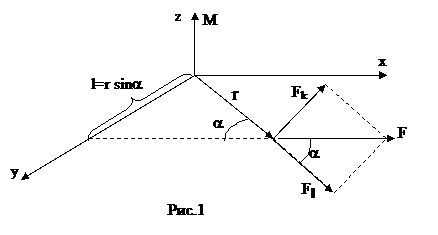 |
Моментом силы относительно точки О называется вектор равный:
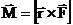
Этот вектор является аксиальным, его направление связано с направлением 
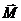
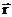 и
и 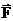 правилом правого винта, то есть вектор
правилом правого винта, то есть вектор  перпендикулярен плоскости содержащей
перпендикулярен плоскости содержащей 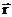 и
и 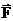 и его направление совпадает с поступательным. движением. буравчика при повороте ручки буравчика от
и его направление совпадает с поступательным. движением. буравчика при повороте ручки буравчика от 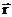 к
к 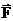 в сторону наименьшего угла.
в сторону наименьшего угла.
В данном случае вектор  направлен по оси Z.
направлен по оси Z.
Если тело может вращаться относительно точки О произвольным образом, то под. действием силы F оно будет вращаться вокруг оси, совпадающей. с направлением момента силы относительно данной точки.
Величина момента силы равна
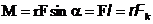
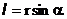 - плечо силы, - это расстояние от точки О до прямой, вдоль которой действует сила
- плечо силы, - это расстояние от точки О до прямой, вдоль которой действует сила
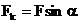 - касательная составляющая силы, перпендикулярная к
- касательная составляющая силы, перпендикулярная к 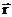 .
.
Если a=0, то есть 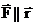 , то M=0.
, то M=0.
Следовательно, сила, проходящая через точку О, не вызывает вращения. Любую силу можно разложить на F|| и F^(F^=Fk – касательная составляющая). Момент силы определяется, следовательно, только составляющей Fk и она вызывает вращение тела.
2). Момент силы относительно оси.
Рассмотрим теперь тело, закрепленное в двух неподвижных точках О и О1 так, что оно может вращаться только вокруг оси, проходящей через эти точки.
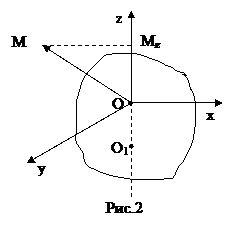 Пусть ОО1 совпадает с осью OZ. Момент силы
Пусть ОО1 совпадает с осью OZ. Момент силы  направлен произвольным образом. Вектор
направлен произвольным образом. Вектор  можно разложить на составляющие Mx, My, Mz., каждая из которых будет стремиться повернуть тело соответственно вокруг осей x, y, z. Составляющие момента Mx и My будут компенсироваться моментами сил реакции, возникающих в точках закрепления. Поэтому вращение будет происходить только под действием составляющей Mz.
можно разложить на составляющие Mx, My, Mz., каждая из которых будет стремиться повернуть тело соответственно вокруг осей x, y, z. Составляющие момента Mx и My будут компенсироваться моментами сил реакции, возникающих в точках закрепления. Поэтому вращение будет происходить только под действием составляющей Mz.
Составляющая вектора  , направленная вдоль оси вращения, называется моментом силы относительно этой оси.
, направленная вдоль оси вращения, называется моментом силы относительно этой оси.
Строго говоря, момент силы относительно оси является скалярной величиной. Однако часто бывает удобно его тоже рассматривать как вектор, который может иметь только два возможных направления, соответствующих вращению по или против часовой стрелки. Если момент силы вызывает вращение тела по часовой стрелке, то он считается положительным, если против – отрицательным.
Если на тело, закрепленное на оси, действуют несколько моментов сил, то суммарное их действие будет эквивалентно действию одного момента  , равного сумме отдельных моментов
, равного сумме отдельных моментов
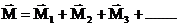
Фактически это не векторная сумма, а алгебраическая. Здесь знаки  положительные или отрицательные.
положительные или отрицательные.
Рассмотрим суммарный момент внутренних сил.
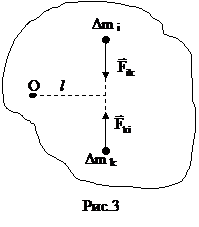
Выделим внутри некоторого тела две элементарные массы Dmi и Dmk.
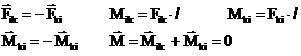 |
Силы, с которыми взаимодействуют друг с другом две любые элементарные массы лежат на одной и той же прямой. Их моменты относительно произвольной оси О равны по величине и противоположны по направлению.
Таким образом, моменты внутренних сил попарно уравновешивают друг друга и сумма моментов всех внутренних сил для любой системы материальных точек всегда равна нулю.
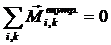 |
Date: 2015-07-22; view: 369; Нарушение авторских прав