Теория удара

БИТЬ ИЛИ НЕ БИТЬ?

Ваваев Михаил, май 2008г.

Аннотация

В статье приведена краткая теория удара и биомеханика ударных действий в спорте. Последняя часть статьи посвящена вопросу боксерского удара в перчатке и голым кулаком, как фактора риска сотрясения мозга. Проанализированы две статьи, исследовавшие параметры боксерских ударов по мешку и манекену, и сделана попытка проанализировать травмоопасность ударов в голову голым кулаком, по сравнению с ударами в боксерской перчатке.

Теория удара

Ударом в механике называется кратковременное взаимодействие тел, в результате которого изменяются их скорости. Ударная сила зависит, согласно закону Ньютона, от эффективной массы ударяющего тела и его ускорения:

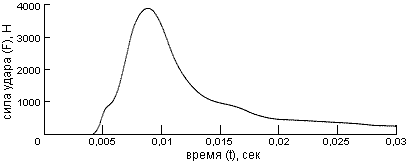
Рис. 1 - Кривая развития силы удара во времени.

где
F - сила,
m - масса,
a - ускорение.

Если рассматривать удар во времени, то взаимодействие длится очень короткое время – от десятитысячных (мгновенные квазиупругие удары), до десятых долей секунды (неупругие удары). Ударная сила в начале удара быстро возрастает до наибольшего значения, а затем падает до нуля (рис. 1). Максимальное ее значение может быть очень большим. Однако основной мерой ударного взаимодействия является не сила, а ударный импульс, численно равный площади под кривой F(t). Он может быть вычислен как интеграл:

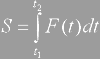
(2)

где
S – ударный импульс,
t1 и t2 – время начала и конца удара,
F(t) – зависимость ударной силы F от времени t.

Так как процесс соударения длится очень короткое время, то в нашем случае его можно рассматривать как мгновенное изменение скоростей соударяющихся тел.
В процессе удара, как и в любых явлениях природы должен соблюдаться закон сохранения энергии. Поэтому закономерно записать следующее уравнение:

где
E1 и E2 – кинетические энергии первого и второго тела до удара,
E'1 и E'2 – кинетические энергии после удара,
E1п и E2п – энергии потерь при ударе в первом и во втором теле.

Соотношение между кинетической энергией после удара и энергией потерь составляет одну из основных проблем теории удара.

Последовательность механических явлений при ударе такова, что сначала происходит деформация тел, во время которой кинетическая энергия движения переходит в потенциальную энергию упругой деформации. Затем потенциальная энергия переходит обратно в кинетическую. В зависимости от того, какая часть потенциальной энергии переходит в кинетическую, а какая теряется, рассеиваясь на нагрев и деформацию, различают три вида удара:

1. Абсолютно упругий удар – вся механическая энергия сохраняется. Это идеализированная модель соударения, однако, в некоторых случаях, например в случае ударов бильярдных шаров, картина соударения близка к абсолютно упругому удару.
2. Абсолютно неупругий удар – энергия деформации полностью переходит в тепло. Пример: приземление в прыжках и соскоках, удар шарика из пластилина в стену и т. п. При абсолютно неупругом ударе скорости взаимодействующих тел после удара равны (тела слипаются).
3. Частично неупругий удар — часть энергии упругой деформации переходит в кинетическую энергию движения.

В реальности все удары являются либо абсолютно, либо частично неупругими. Ньютон предложил характеризовать неупругий удар так называемым коэффициентом восстановления. Он равен отношению скоростей взаимодействующих тел после и до удара. Чем этот коэффициент меньше, тем больше энергии расходуется на некинетические составляющие E1п и E2п (нагрев, деформация). Теоретически этот коэффициент получить нельзя, он определяется опытным путем и может быть рассчитан по следующей формуле:

(4)

где
v1, v2 – скорости тел до удара,
v'1, v'2 – после удара.

При k = 0 удар будет абсолютно неупругим, а при k = 1 – абсолютно упругим. Коэффициент восстановления зависит от упругих свойств соударяемых тел. Например, он будет различен при ударе теннисного мяча о разные грунты и ракетки разных типов и качества. Коэффициент восстановления не является просто характеристикой материала, так как зависит еще и от скорости ударного взаимодействия - с увеличением скорости он уменьшается. В справочниках приведены значения коэффициента восстановления для некоторых материалов для скорости удара менее 3 м/с.

Date: 2015-06-11; view: 768; Нарушение авторских прав