Уравнения движения несжимаемой жидкости

2.1.1 Кинематика течения идеальной жидкости

Идеальной считается жидкость, которая не обладает вязкостью и, следовательно, силами внутреннего трения.

Представим себе некоторую область пространства, заполненную потоком невязкой жидкости. Зафиксируем момент времени и рассмотрим век значения скорости потока в каждой точке. Мы получили так называемо скоростей". В этом поле можно провести семейство кривых, обладают свойством, что в каждой точке такой кривой касательная совпадает с направлением скорости. Это семейство "линий тока". Если линии тока со временем не смещаются в пространстве, течение является стационарным.

Проведём далее в рассматриваемой области некий замкнутый контур "Т", а через все его точки - семейство линий тока. Получим "трубку тока" (рис3):

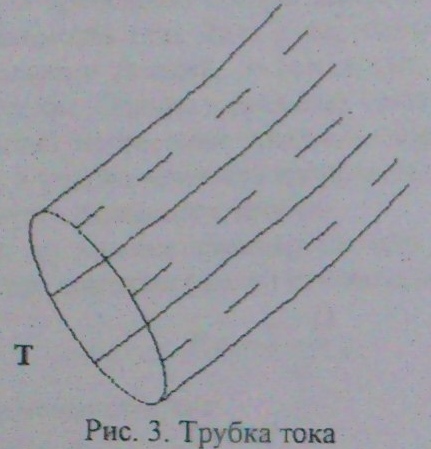
Ясно, что поток жидкости внутри трубки тока не меняется, поскольку близ её поверхности частички жидкости движутся по касательным и не пересекают стенки трубки.

Рассмотрим два неодинаковых сечения трубки тока S₁ и S₂

Пусть d т₁ = ρ₁ S₁ dt - масса жидкости, втекающей в рассматриваемый объём за время dt, а d т₂ = ρ₂ S₂ dt - масса жидкости, покидающая его за тот же промежуток времени через сечение S₂

В силу неизменности потока

dт₁ = dт₂ => ρ₁ S₁ V_{1 =} ρ₂ S₂ V₂

Тогда =

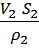
где V₁,V₂ - скорости движения жидкости в сечениях S_1, S₂

ρ_1, ρ₂ - плотности жидкости в тех же сечениях.

Следовательно, при выполнении условия несжимаемости жидкости ρ_{1 =} ρ_{2 = CONST} имеем =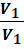

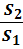
т.е. скорости жидкости в разных сечениях жидкости обратно пропорциональны площади этих сечений.

2.1.2 Профиль скоростей при движении вязкой жидкости

по круглой трубе.

Из повседневного опыта хорошо известно, что реальные жидкости и газы обладают вязкостью. Различают коэффициент динамической Па • с и кине-

матической 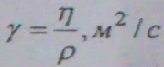вязкости (р - плотность жидкости, кг/м³).

Пусть поток вязкой жидкости течёт по трубе круглого сечения радиуса г„

и длины Ь, к концам которой приложена разность давлений 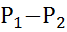. Скорость те­чения жидкости V(г) будет меняться вдоль радиуса трубы: у стенок она равна нулю, а на оси трубы - максимальна. Аналитическая зависимость скорости от радиуса трубы в СИ имеет следующий вид:

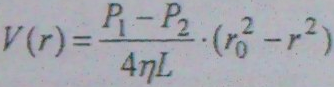(3).

Как видно из уравнения (3), скорость течения прямо пропорциональна приложенному давлению, обратно пропорциональна коэффициенту вязкости жидкости и длине трубы. Сильнее её зависимость от радиуса: скорость течения пропорциональна величине радиуса трубы во второй степени. Подставив г= О, получим выражение для осевой скорости:

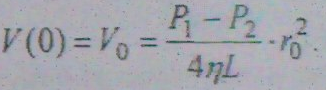(4)

2.1.3. Уравнение для потока вязкой жидкости по трубе. Формула Пуазейля

Используя формулу (3), можно найти выражение для потока вязкой жид­кости через круглую трубу радиусом г₀, длиной L под действием приложенной разности давлений 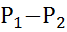. Формула для потока вязкой жидкости впервые была получена Пуазейлем (1799-1869):

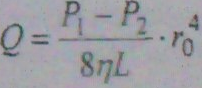(5)

Анализ выражения (5) показывает, что при заданной разности давлений на концах трубы поток очень сильно зависит от её радиуса - как четвёртая сте­пень величины радиуса. Зависимость потока от коэффициента вязкости и дли­ны трубы носит характер обратной пропорциональности.

ИССЛЕДОВАНИЕ ВЕНТИЛЯЦИИ С ПОМОЩЬЮ ЛАБОРАТОРНОГО СТЕНДА

Цель работы - изучение составных частей вентиляционных элементов теории гидродинамики вязкого газа, практики расчёта в газоходах; экспериментальное определение полного и динамического давления, скорости течения газа в различных сечениях, сравнение экспериментальных данных с теоретическими расчётами.

Для её выполнения необходимо:

ü ознакомиться с основами гигиенического нормирования микроклимата,

ü типами вентиляции и устройством центробежного вентилятора;

ü изучить элементарные сведения о гидродинамике вязкой жидкости

ü экспериментально определить полное, статическое и динамическое давления в газоходе;

ü измерить скорости потока в трёх сечениях газохода;

ü по экспериментальным данным рассчитать потери давления в газоходе;

ü сделать вывод о соответствии вентилятора данной вен теме;

ü рассчитать воздухообмен в помещении и сделать вывод о его достаточности с точки зрения гигиены труда.

Отсчёт по шкале верхнего прибора, мм	Отсчёт по шкале нижнего прибора, мм	Скорость потока, м/с
lВН	lВК	lнн	lнк

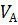
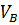
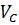
· Расчитываем по формулам полное и динамическое давления

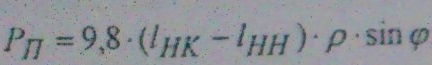
Sinφ = 0.1

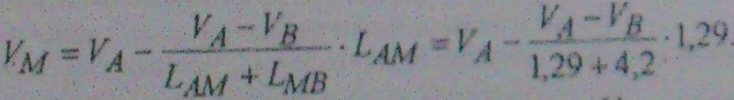
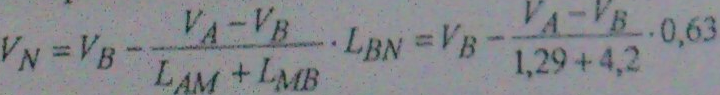
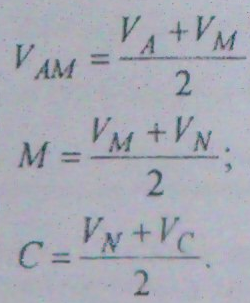
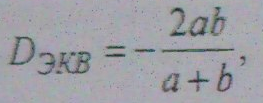
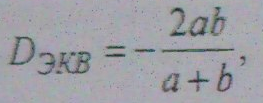
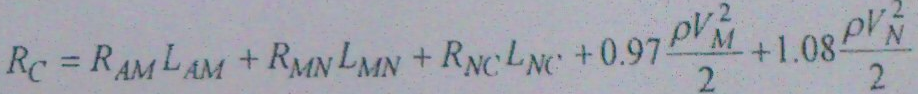
ρ=1.29

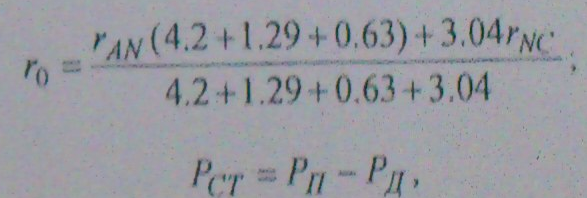
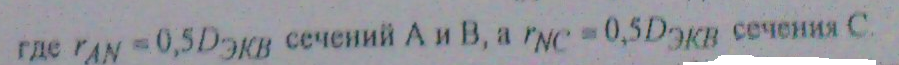
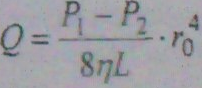
L=4.87 м

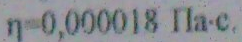
Вывод:

Date: 2015-07-10; view: 1107; Нарушение авторских прав