Лекция 9 Переменные действие-угол

Метод канонических преобразований играет большую роль при исследовании систем, совершающих движения, близкие к периодическим движениям. С его помощью можно получить частоты, характеризующие это движение, не отыскивая самого закона движения системы.

Рассмотрим случай системы с одной степени свободы. Фазовое пространство такой системы является двумерной плоскостью 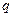, , 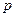и периодические движения могут быть двух различных типов.

В движениях первого типа функци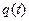и и 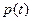являются периодическими функциями с одним и тем же периодом. Точка, изображающая движение в фазовой плоскости, описывает замкнутую кривую. В этом случае говорят, что имеет место случай колебаний. Примером могут служить колебания маятника, Им отвечают замкнутые фазовые кривые, окружающие особые точки типа центр.

В движениях второго типа сама величина 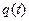является периодической функцией, но когда она изменяется на величину 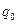, конфигурация системы не меняется. Здесь фазовые кривые не замкнуты и имеют период 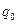, по 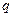. Периодические движения второго типа называются вращениями. Простейшим примером может служить движение твердого тела, вращающегося вокруг неподвижной оси. Случаю вращений отвечают незамкнутые фазовые кривые.

Пусть 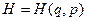- функция Гамильтона имеет одну степень свободы и явно от времени не зависит

Тогда существует обобщенный интеграл энергии H=h, где h – произвольная постоянная.

В уравнении 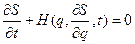положим 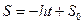, 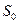не зависит от t. Для нее получим уравнение 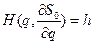. Тогда 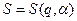, где 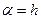- постоянная интеграла H=h. , , .

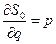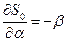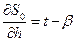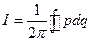Вместо возьмем величину , где интегралы берутся по полным периодам изменения импульсов p как функции соответствующих q.

Идея метода решения задачи заключается в применении канонического преобразования от q_i и p_i к таким переменным, где роль новых импульсов играет специально выбранные постоянные I_i, являющимися функциями постоянных a_i, а новый гамильтониан зависит только от новых импульсов.

С помощью этой величины можно дать новую формулировку движения замкнутых систем.

Величин 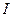называются переменными действия и являются независимыми функциями a_I: 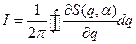, т.е. 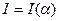. При условии 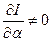из (3) находим 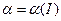. Тогда получаем новую функцию Гамильтона .

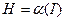Производящая функция канонического преобразования будет функция

.

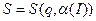Таким образом, алгоритм введения переменных действие-угол в гамильтоновой системе с одной степенью свободы выглядит так. Из уравнения 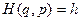находим функцию 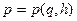, а затем вычисляем переменную I как функцию h:

.

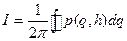Обращение функции 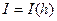дает 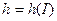. Производящая функция преобразования будет функция, определяемая равенством

.

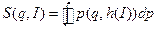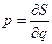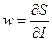Неявно замена задается формулами , , где 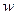-угловая переменная.

Новая функция Гамильтона 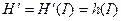. В переменных действие угол уравнения движения будут такими:

, .

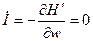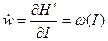Отсюда следует, что 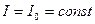, 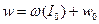. Величина w называется частотой рассматриваемого периодического движения.

Отметим, что когда координата совершает полный цикл изменения, то угловая переменная 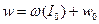возрастает на 2p. Обозначая через D 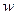приращение 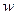за цикл изменения q, имеем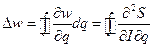

Вынося производную по I за знак интеграла и приняв во внимание формулу 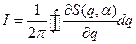, получим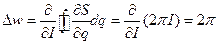

Это поясняет название величины w угловой переменной.

Пример. Твердое тело, вращающееся вокруг неподвижной оси. А – момент инерции, j -угол поворота вокруг оси. 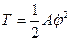, P=0, , .

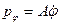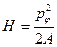Из уравнения H=h находим и, следовательно,

;

, , ;

, .

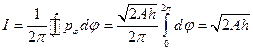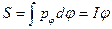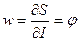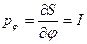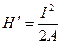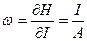Пример. Гармонический осциллятор частоты w.

Из уравнения H=h имеем 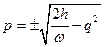. Если в правой части равенства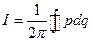

Сделать замену 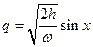, то получим 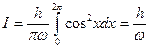, т.е. .

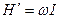Для производящей функции замены имеем выражение

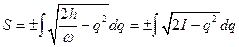
Из формул (7) находим замену, вводящую переменные действие-угол, в виде

,

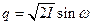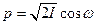
Адиабатические инварианты.

Рассмотрим механическую систему, совершающую одномерное финитное движение и характеризующуюся некоторым параметром l, определяющим свойства самой системы или внешнего поля, в котором оно находится.

Предположим, что параметр l под влиянием каких-либо внешних причин медленно (адиабатически) меняется со временем, т.е.

.

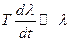Такая система не является замкнутой и ее энергия Е не сохраняется.

Но в силу медленности изменения l можно утверждать, что скорость изменения энергии пропорционально скорости изменения параметра l. Это значит, что энергия системы ведет себя при изменении l как некоторая функция l. Другими словами, существует такая комбинация из Е и l, которая остается при движении системы неизменной; эту величину называют адиабатическим инвариантом.

Вывод соотношений для задачи математического маятника с медленно меняющейся длиной подвеса.

Пример. В качестве примера определим адиабатический инвариант для одномерного осциллятора. Его функция Гамильтона 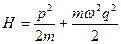, где w - собственная частота осциллятора. Уравнение фазовой траектории дается законом сохранения энергии H(p,q) =E.

Это есть эллипс с полуосям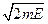и и 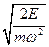и его площадь (деленная на 2p) .

Адиабатическая инвариантность этой величины означает, что при изменении параметров осциллятора его энергия меняется пропорционально частоте.

Если обе p_i и q_i являются периодическими функциями с одинаковым периодом, I_i равна площади фигуры, ограниченной проекцией фазовой траектории на плоскость (p_i q_i) (замкнутая кривая). Если же p_i(q_i) периодическая, q_i неограниченно возрастает, то I_i равна площади фигуры, ограниченной кривой p_i(q_i), осью q_i и двумя ординатами, соответствующей полному периоду этой функции.

Date: 2015-07-10; view: 1204; Нарушение авторских прав