Вставка ключа в Б-дерево

Вставка ключа в Б-дерево существенно сложнее вставки в бинарное дерево поиска. Как и в случае бинарных деревьев поиска, ищем позицию листа, в который будет вставлен новый ключ. Однако при работе с Б-деревом нельзя просто создать новый лист и вставить в него ключ, поскольку будут нарушаться свойства Б-дерева. Вместо этого вставляем новый ключ в уже существующий лист. Поскольку вставить новый ключ в заполненный лист невозможно, вводим новую операцию – разбиение заполненного (т.е. содержащего 2t-1 ключей) узла на два, каждый из которых содержит по t-1 ключей (разбиваем на 2 по t-1). Средний элемент (для которого t-1 первых ключей меньше его, а t-1 последних больше) перемещается в родительский узел, где становится родительской точкой для двух вновь образовавшихся поддеревьев. Соответственно, если родительский узел также был заполнен – то опять приходится разбивать. И так далее до корня(если разбивается корень – то появляется новый корень и глубина дерева увеличивается).

Как и в случае бинарного дерева поиска, в Б-дереве вполне можно осуществить вставку за один нисходящий проход от корня к листу. Для этого не нужно выяснять, требуется ли разбить узел, в который должен вставляться новый ключ. Вместо этого при проходе от корня к листьям в поисках позиции для нового ключа разбиваем все заполненные узлы, через которые проходим(включая лист). Тем самым гарантируется, что если необходимо разбить какой-то узел, то его родительский узел не будет заполнен.

Пример. Возьмем нарисованное ниже дерево и добавим в него элемент 13.

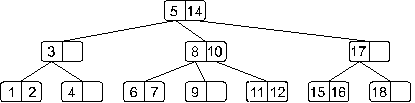
Двигаясь от корня, найдем узел, в который следует добавить искомый элемент. Таким узлом в нашем случае окажется узел, содержащий элементы 11 и 12. Добавим

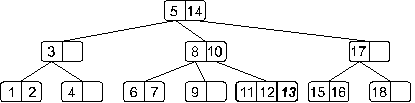
Получили переполнение. При его обработке узел, содержащий элементы 11, 12 и 13 разделится на две части: узел с элементом 11 и узел с элементом 13, – а средний элемент 12 будет вынесен на верхний уровень.

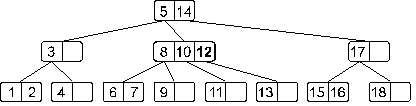
Опять получили переполнение, при обработке которого узел, содержащий элементы 8, 10 и 12 разделится на два узла: узел с элементом 8 и узел с элементом 12, – а средний элемент 10 будет вынесен на верхний уровень.

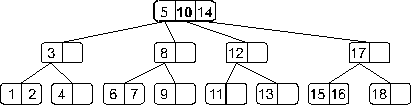
Теперь получили переполнение в корне дерева. Как оговаривали ранее этот случай надо обработать отдельно. Это связано с тем, что здесь необходимо будет создать новый корень, в который во время деления будет вынесен средний элемент:

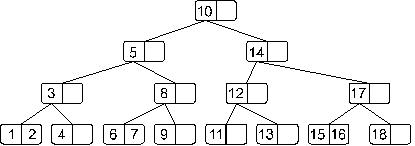
Теперь полученное дерево не имеет переполнения.

В этом случае, как и при поиске, время обработки страницы поиска есть величина постоянная, пропорциональная размеру страницы, а значит, сложность алгоритма добавления в Б-дерево будет также T(h), где h – глубина дерева.

Date: 2015-06-11; view: 430; Нарушение авторских прав