
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретическое обоснование
|
|
Лабораторная работа №19
Решение задачи линейного программирования в MS Excel
(2 часа)
1. Цель и содержание: изучение методики решения задачи линейного программирования с использованием табличного процессора Excel 2010.
Теоретическое обоснование
2.1. Постановка задачи линейного программирования. Задача линейного программирования является достаточно распространенной задачей принятия оптимальных решений, особенно в экономике. Нахождение оптимума многомерных экономических функций сводится к поиску экстремумов функции. При этом нужно отличать глобальные и локальные экстремумы. Отсутствие наглядных графических представлений многомерных функций вынуждает применять численные методы нахождения оптимальных решений методами линейного программирования. С этой задаче успешно справляется пакет табличного процессора Excel 2010. Решение этой задачи рассмотрим на примере задачи распределения ресурсов.
Задача линейного программирования, которая является частным случаем задачи оптимизации, записывается следующим образом. Необходимо решить систему неравенств описывающих запасы ресурсов и экстремум функции выпуска продукции F:
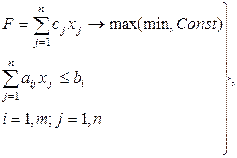 (1)
(1)
где F – функция цели;
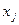 – количество выпускаемой продукции j -го типа;
– количество выпускаемой продукции j -го типа;
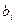 – количество располагаемого ресурса i- го вида;
– количество располагаемого ресурса i- го вида;
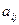 – норма расхода i- го ресурса для выпуска единицы продукции j -го типа;
– норма расхода i- го ресурса для выпуска единицы продукции j -го типа;
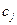 – прибыль, получаемая от реализации единицы продукции j -го типа.
– прибыль, получаемая от реализации единицы продукции j -го типа.
2.1.1. Задача распределения ресурсов. Частным случаем задачи линейного программирования является задача распределения ресурсов. Если финансы, оборудование, сырье и даже людей считать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования.
Рассмотрим следующий пример.
Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, финансовые, сырье. Количество ресурса каждого типа, необходимое для выпуска единицы продукции, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 1. Там же приведено наличие располагаемого ресурса.
Таблица 1
| Ресурс | Прод1 | Прод2 | Прод3 | Прод4 | Ограничения | |
| Прибыль | = | max | ||||
| Трудовые | <= | |||||
| Сырье | <= | |||||
| Финансы | <= |
Как видно из таблицы 1, для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 6 x1 единиц сырья, где x1 – количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:
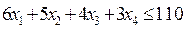 (2)
(2)
В этом ограничении левая часть равна величине требующегося ресурса, а правая показывает количество имеющегося ресурса.
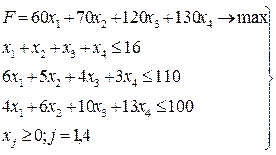 (3)
(3)
Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид: (3).
Аналитическое решение задачи линейного программирования осуществляется с помощью симплекс-метода. В Excel имеется математический аппарат, реализующий основные идеи данного метода. Решение задачи с помощью Excel будем рассматривать на примере задачи, математическая модель которой имеет вид (3).
Date: 2015-07-10; view: 286; Нарушение авторских прав