
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Критерий линейной зависимости векторов
|
|
Необходимым и достаточным условием линейной зависимости двух
векторов является их коллинеарность.
2. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается каккоммутативная и линейная по каждому сомножителю.
Свойства скалярного произведения: 

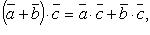
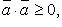
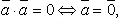
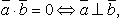
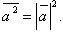
3. Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости[1].
Необходимым и достаточным условием линейной зависимости трехвекторов является их компланарность.Любые четыре вектора линейно зависимы. Базисом в пространстве называется любаяупорядоченная тройка некомпланарных векторов. Базис в пространстве позволяет однозначно сопоставить каждому векторуупорядоченную тройку чисел – коэффициенты представления этого вектора в виделинейной комбинации векторов базиса. Наоборот, каждой упорядоченной тройкечисел при помощи базиса
при помощи базиса 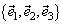 мы сопоставим вектор
мы сопоставим вектор 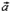 , еслисоставим линейную комбинацию
, еслисоставим линейную комбинацию 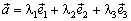 Ортогональный базис называется ортонормированным, если еговекторы по длине равны единице. Для ортонормированного базиса в пространствечасто используют обозначения
Ортогональный базис называется ортонормированным, если еговекторы по длине равны единице. Для ортонормированного базиса в пространствечасто используют обозначения 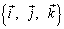 . Теорема: В ортонормированном базисе координаты векторов естьсоответствующие ортогональные проекции этого вектора на направлениякоординатных векторов. Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо.
. Теорема: В ортонормированном базисе координаты векторов естьсоответствующие ортогональные проекции этого вектора на направлениякоординатных векторов. Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо. Четыре угла (I, II, III, IV), образованные осями координат X ' X и Y ' Y, называются координатными углами или квадрантами (см. рис. 1).
если векторы 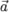 и
и  относительно ортонормированного базиса на плоскости имеют координаты
относительно ортонормированного базиса на плоскости имеют координаты 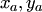 и
и 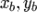 соответственно, то скалярное произведение этих векторов вычисляется по формуле
соответственно, то скалярное произведение этих векторов вычисляется по формуле
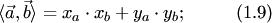
4. Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими
свойствами: 
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах. Необходимым и достаточным условием коллинеарности ненулевого вектора 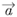 и вектора
и вектора 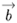 является существование такого числа
является существование такого числа 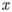 , которое удовлетворяет равенству
, которое удовлетворяет равенству 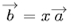 .
.
Если два вектора  и
и 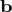 определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены вортонормированном базисе
определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены вортонормированном базисе
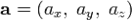
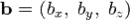
а система координат правая, то их векторное произведение имеет вид
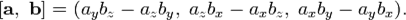
Для запоминания этой формулы удобно использовать определитель:

5. Сме́шанное произведе́ние 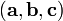 векторов
векторов 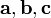 — скалярное произведение вектора
— скалярное произведение вектора  на векторное произведениевекторов
на векторное произведениевекторов 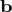 и
и  :
:
 .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр(точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами 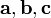 .
.
При перестановке двух множителей смешанное произведение изменяет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение не изменяется:
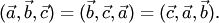
Смешанное произведение линейно по любому множителю.
Смешанное произведение 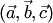 равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы  компланарны.
компланарны.
1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
§ Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
§ Смешанное произведение компланарных векторов  . Это — критерий компланарности трёх векторов.
. Это — критерий компланарности трёх векторов.
§ Компланарные векторы — линейно зависимы. Это — тоже критерий компланарности.
§ Существуют действительные числа 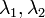 такие, что
такие, что 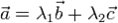 для компланарных
для компланарных 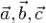 , за исключением случаев
, за исключением случаев 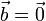 или
или  . Это — переформулировка предыдущего свойства и тоже критерий компланарности.
. Это — переформулировка предыдущего свойства и тоже критерий компланарности.
§ В 3-мерном пространстве 3 некомпланарных вектора 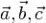 образуют базис. То есть любой вектор
образуют базис. То есть любой вектор  можно представить в виде:
можно представить в виде: 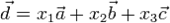 . Тогда
. Тогда  будут координатами
будут координатами  в данном базисе.
в данном базисе.
Смешанное произведение 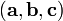 в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 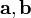 и
и  :
:
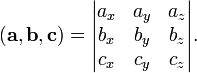
§ 6. Общее уравнение (полное) плоскости
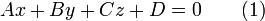
где  и
и 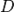 — постоянные, причём
— постоянные, причём 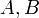 и
и 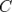 одновременно не равны нулю; в векторной форме:
одновременно не равны нулю; в векторной форме:

где  — радиус-вектор точки
— радиус-вектор точки 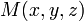 , вектор
, вектор 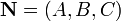 перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора
перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора 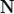 :
:
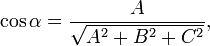
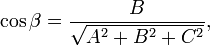

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При  плоскость проходит через начало координат, при
плоскость проходит через начало координат, при  (или
(или  ,
,  ) П. параллельна оси
) П. параллельна оси 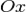 (соответственно
(соответственно  или
или 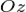 ). При
). При 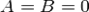 (
(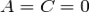 , или
, или 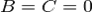 ) плоскость параллельна плоскости
) плоскость параллельна плоскости 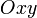 (соответственно
(соответственно  или
или 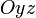 ).
).
§ Уравнение плоскости в отрезках:

где 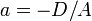 ,
, 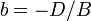 ,
, 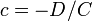 — отрезки, отсекаемые плоскостью на осях
— отрезки, отсекаемые плоскостью на осях 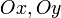 и
и 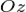 .
.
§ Уравнение плоскости, проходящей через точку 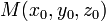 перпендикулярно вектору нормали
перпендикулярно вектору нормали 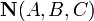 :
:
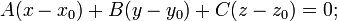
в векторной форме:
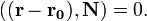
(смешанное произведение векторов), иначе
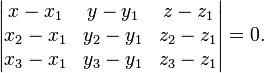
§ Нормальное (нормированное) уравнение плоскости
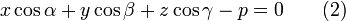
§ Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
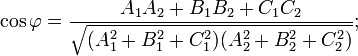
Если в векторной форме, то
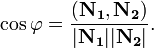
§ Плоскости параллельны, если
 или
или  (Векторное произведение)
(Векторное произведение)
§ Плоскости перпендикулярны, если
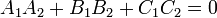 или
или 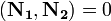 . (Скалярное произведение)
. (Скалярное произведение)
7. Уравнение плоскости, проходящей через три заданные точки 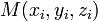 , не лежащие на одной прямой:
, не лежащие на одной прямой:

8.Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, чторасстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
§ Отклонение точки 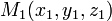 от плоскости заданной нормированным уравнением
от плоскости заданной нормированным уравнением 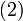
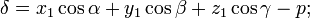
 ,если
,если 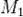 и начало координат лежат по разные стороны плоскости, в противоположном случае
и начало координат лежат по разные стороны плоскости, в противоположном случае  . Расстояние от точки до плоскости равно
. Расстояние от точки до плоскости равно 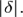
§ Расстояние 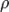 от точки
от точки 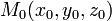 , до плоскости, заданной уравнением
, до плоскости, заданной уравнением  , вычисляется по формуле:
, вычисляется по формуле:
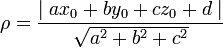
9. Пучок плоскостей — уравнение любой П., проходящей через линию пересечения двух плоскостей
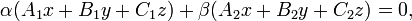
где α и β — любые числа, не равные одновременно нулю.
Для того чтобы три плоскости, заданные своими общими уравнениями A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0, A3x+B3y+C3z+D3=0 относительно ПДСК принадлежали одному пучку, собственному или несобственному, необходимо и достаточно, чтобы ранг матрицы 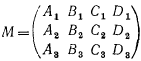 был равен или двум, или единице.
был равен или двум, или единице.
Теорема 2. Пусть относительно ПДСК заданы две плоскости π1 и π2 своими общими уравнениями: A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Для того чтобы плоскость π3, заданная относительно ПДСК своим общим уравнением A3x+B3y+C3z+D3=0, принадлежала пучку, образованному плоскостями π1 и π2, необходимо и достаточно, чтобы левая часть уравнения плоскости π3 представлялась как линейная комбинация левых частей уравнений плоскостей π1 и π2.
10. Векторное параметрическое уравнение прямой в пространстве:
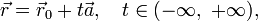
где 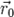 — радиус-вектор некоторой фиксированной точки M 0, лежащей на прямой,
— радиус-вектор некоторой фиксированной точки M 0, лежащей на прямой, 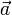 — ненулевой вектор, коллинеарный этой прямой,
— ненулевой вектор, коллинеарный этой прямой, 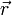 — радиус-вектор произвольной точки прямой.
— радиус-вектор произвольной точки прямой.
Параметрическое уравнение прямой в пространстве:
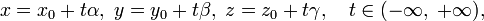
где  — координаты некоторой фиксированной точки M 0, лежащей на прямой;
— координаты некоторой фиксированной точки M 0, лежащей на прямой; 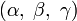 — координаты вектора,коллинеарного этой прямой.
— координаты вектора,коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
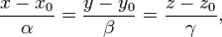
где  — координаты некоторой фиксированной точки M 0, лежащей на прямой;
— координаты некоторой фиксированной точки M 0, лежащей на прямой; 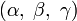 — координаты вектора,коллинеарного этой прямой.
— координаты вектора,коллинеарного этой прямой.
Общее векторное уравнение прямой в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
 и
и 
то уравнение прямой можно задать системой этих уравнений:

Угол между прямой и плоскостью находят по формуле:

|
где (А;В;С;) координаты нормального вектора плоскости
(l;m;n;) координаты направляющего вектора прямой
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k 1 = k 2. (8)
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
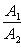
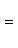
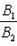
 (9)
(9)
Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
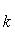
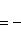
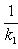
 (10)
(10)
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
A 1 A 2 + B 1 B 2 = 0. (12)
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой в этой плоскости. Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости. Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
11.
12. В пространстве расстояние от точки 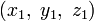 до прямой, заданной параметрическим уравнением
до прямой, заданной параметрическим уравнением
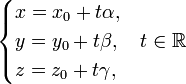
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент t этой точки может быть найден по формуле
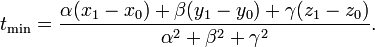
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые. 
В координатах
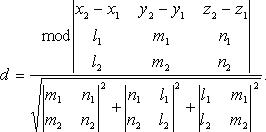
Date: 2015-07-02; view: 1658; Нарушение авторских прав