
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тесты по аналитической геометрии
|
|
1.Векторы 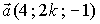 и
и 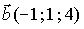 перпендикулярны, если k равно…:
перпендикулярны, если k равно…:
| –4 | –2 |
Прямая проходит через точки О(0;0) и В(–2;1). Тогда ее угловой коэффициент равен…
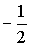
| –2 | 
|
Уравнение прямой, проходящей через точку N(2;0;–1) перпендикулярно плоскости 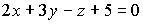 , имеет вид…:
, имеет вид…:
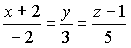
| 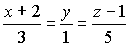
| 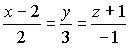
| 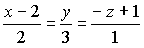
|
Расстояние между точками A(1, 2) и B(k, – 2) равно 5 при k равном …:
Если уравнение гиперболы имеет вид 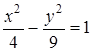 , то длина ее действительной полуоси равна…
, то длина ее действительной полуоси равна…
Нормальный вектор плоскости 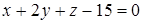 имеет координаты…
имеет координаты…
| (1;2;1) | (2;1;–15) | (1;2;–15) | (1;1;–15) |
Векторы 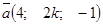 и
и 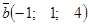 перпендикулярны, если k равно…:
перпендикулярны, если k равно…:
| –2 | –4 |
Нормальный вектор плоскости 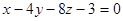 имеет координаты…:
имеет координаты…:
| (1;–4;8) | (1;–4;–8) | (–4;–8;–3) | (1;–4;–3) |
Уравнение прямой, проведенной из точки N(2;0;–1) перпендикулярно плоскости 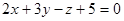 , имеет вид…:
, имеет вид…:
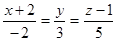
| 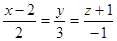
| 
| 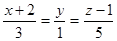
|
Даны точки A(2; 3) и B(– 6; 5). Тогда координаты середины отрезка AB равны…:
| (–4; 1) | (– 2; 8) | (– 4; 8) | (– 2; 4) |
Векторы 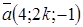 и
и 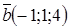 перпендикулярны, если k равно…
перпендикулярны, если k равно…
| -4 | -2 |
Если уравнение гиперболы имеет вид 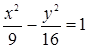 , то длина ее действительной полуоси равна…:
, то длина ее действительной полуоси равна…:
Уравнение прямой, проведенной из точки N(2;0;–1) перпендикулярно плоскости 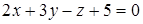 , имеет вид…:
, имеет вид…:
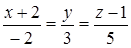
| 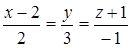
| 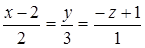
| 
|
Даны точки A(2; 3) и B(– 6; 5). Тогда координаты середины отрезка AB равны...:
| (– 4; 8) | (–4; 1) | (– 2; 8) | (– 2; 4) |
Расстояние между точками В(–3; –4) и D(6; 8) равно…:
Радиус окружности, заданной уравнением 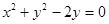 , равен…:
, равен…:
| –1 |
Координата x 0 точки А (х 0; 1; 7), принадлежащей плоскости 5 x + y – z +1=0, равна…:
Даны точки A=(5; – 8) и B=(– 3; 4). Тогда ордината середины отрезка AB равна…:
| –4 | –2 |
Нормальный вектор плоскости 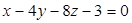 имеет координаты…:
имеет координаты…:
| (1;–4;8) | (1;–4;–8) | (1;–4;–3) | (–4;–8;–3) |
Уравнение прямой, проведенной из точки N(2;0;–1) перпендикулярно плоскости 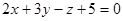 , имеет вид…:
, имеет вид…:
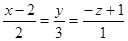
| 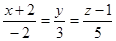
| 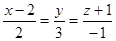
| 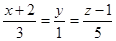
|
Даны точки A(2; 3) и B(– 6; 5). Тогда координаты середины отрезка AB равны…:
| (– 4; 8) | (–4; 1) | (– 2; 8) | (– 2; 4) |
Чему равно расстояние между точками 
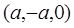 и
и 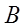
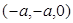 ?
?
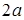 ; ;
| 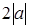 ; ;
| 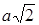 ; ;
| 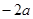 ; ;
| 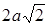 . .
|
Найти расстояние между точками 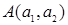 и
и 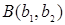 .
.
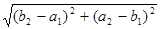 ; ;
|
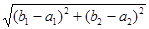 ; ;
|
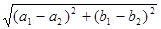 ; ;
|
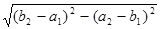 ; ;
|
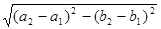 . .
|
Для точки 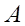 (-3, 4) найти точку, симметричную относительно оси абсцисс.
(-3, 4) найти точку, симметричную относительно оси абсцисс.
| (3, -4); | (-3, -4); | (3, 4); | (4, -4); | (-3, 3). |
Для точки 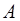 (-3, 4) найти точку, симметричную относительно оси ординат.
(-3, 4) найти точку, симметричную относительно оси ординат.
| (3, -4); | (-3, -4); | (3, 4); | (4, -4); | (-3, 3). |
Для точки 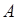 (-3, 4) найти точку, симметричную относительно начала координат.
(-3, 4) найти точку, симметричную относительно начала координат.
| (3, -4); | (-3, -4); | (3, 4); | (4, -4); | (-3, 3). |
Где лежат точки пространства, для которых координаты 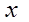 и
и 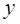 равны нулю?
равны нулю?
на оси 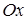 ; ;
| на оси 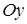 ; ;
| на оси 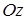 ; ;
| на плоскости 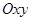 ; ;
| на плоскости 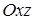 . .
|
Найти координаты середины отрезка 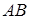 , если
, если 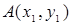 ,
, 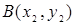 .
.
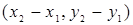 ; ;
|
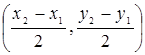 ; ;
|
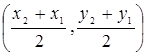 ; ;
|
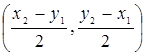 ; ;
|
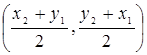
|
Чему равны координаты точки 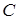 , лежащей в середине отрезка
, лежащей в середине отрезка 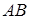 , если известны координаты
, если известны координаты 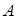 (-1, 3, 0) и
(-1, 3, 0) и 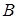 (-3, 0, 4)?
(-3, 0, 4)?
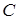 (-2, -1.5, -2); (-2, -1.5, -2);
|
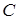 (-2, 1.5, 2); (-2, 1.5, 2);
|
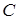 (-4, 3, 4); (-4, 3, 4);
|
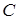 (-1, -1.5, 2); (-1, -1.5, 2);
|
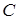 (1, 1.5, 2). (1, 1.5, 2).
|
Чему равны координаты вектора 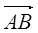 , если известны координаты
, если известны координаты 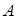 (2, -3, 4) и
(2, -3, 4) и 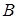 (-1, 0, 5)?
(-1, 0, 5)?
| (3, -3, -1); |
| (-3, 3, 1); |
| (1, -3, 9); |
| (-3, -3, 1); |
| (-2, 0, 20). |
Чему равно скалярное произведение векторов 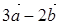 и
и 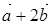 , если известно, что векторы
, если известно, что векторы 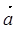 и
и 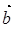 образуют угол
образуют угол 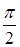 и
и  ;
;  ?
?
| 11; | 17; | 25; | 13; | 0. |
Чему равен угол между векторами 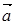 (1, 1, 3) и
(1, 1, 3) и 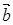 (0, 0, 2)?
(0, 0, 2)?
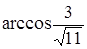 ; ;
| 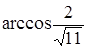 ; ;
| 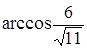 ; ;
| 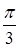 ; ;
| 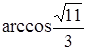 . .
|
Определить угловой коэффициент в уравнении прямой 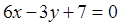 ?
?
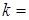 -3; -3;
| 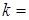 6; 6;
| 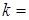 7; 7;
| 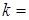 -2; -2;
| 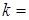 2. 2.
|
Определить угловой коэффициент в уравнении прямой 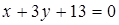 .
.
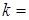 1; 1;
| 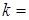  ; ;
| 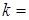 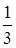 ; ;
| 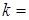 3; 3;
| 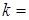 13. 13.
|
Какой смысл имеют коэффициенты 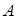 и
и 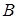 в общем уравнении прямой:
в общем уравнении прямой: 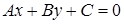 ?
?
это координаты точек, в которых прямая пересекает оси 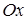 и и 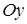 ; ;
|
| это координаты направляющего вектора, параллельного данной прямой; |
| это координаты направляющего вектора, перпендикулярного данной прямой; |
| это координаты точки, через которую проходит данная прямая; |
| это направляющие косинусы. |
Чему равно расстояние от прямой 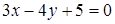 до начала координат?
до начала координат?
| -1 |
Выберите ответ, в котором записано условие ортогональности двух прямых: 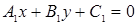 и
и 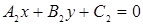 .
.
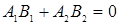 ; ;
|
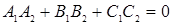 ; ;
|
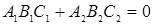 ; ;
|
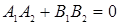 ; ;
|
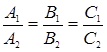 . .
|
Выберите ответ, в котором записано уравнение прямой, ортогональной заданной прямой  .
.
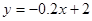
| 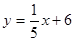
| 
| 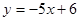
| 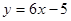
|
Выберите ответ, в котором записано условие параллельности двух прямых: 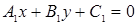 и
и 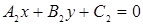 .
.
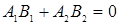 ; ;
|
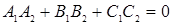 ; ;
|
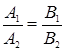
|
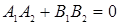 ; ;
|
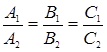 . .
|
Угол между двумя прямыми 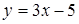 и
и 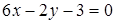 равен…
равен…
| 0; | 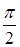 ; ;
| 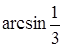 ; ;
| 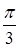 ; ;
| 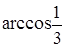 . .
|
Найти уравнение прямой, проходящей через начало координат и перпендикулярной прямой, заданной уравнением 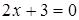 .
.
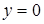 ; ;
| 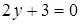 ; ;
| 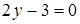 ; ;
| 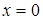 ; ;
|  . .
|
Коэффициенты 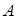 ,
, 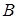 и
и 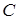 в общем уравнении плоскости:
в общем уравнении плоскости: 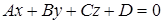 это…
это…
координаты точек, в которых плоскость пересекает оси 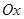 , , 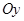 и и 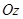 ; ;
|
| координаты направляющего вектора, параллельного данной плоскости; |
| координаты направляющего вектора, перпендикулярного данной плоскости; |
| координаты точки, через которую проходит данная плоскость; |
| направляющие косинусы. |
Расстояние от плоскости 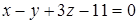 до начала координат равно…
до начала координат равно…
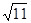 ; ;
| 11; | 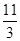 ; ;
| 1; | 3. |
Определите расположение плоскости 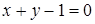 относительно осей координат.
относительно осей координат.
параллельна оси 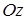 ; ;
|
параллельна оси 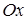 ; ;
|
параллельна оси 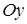 ; ;
|
угол с осью 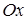 равен равен 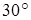 ; ;
|
угол с осью 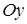 равен равен 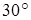 . .
|
Определите расположение плоскости 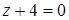 относительно плоскостей
относительно плоскостей 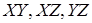 .
.
параллельна плоскости 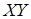
|
параллельна плоскости 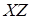
|
параллельна плоскости 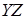
|
угол с плоскостью 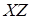 равен равен 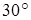
|
угол с плоскостью 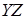 равен равен 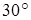
|
Выберите ответ, в котором записано условие ортогональности двух плоскостей: 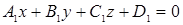 и
и 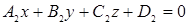 .
.
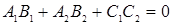 ; ;
|
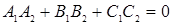 ; ;
|
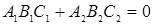 ; ;
|
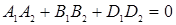 ; ;
|
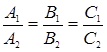 . .
|
Выберите ответ, в котором записано уравнение плоскости, параллельной заданной плоскости 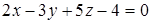 .
.
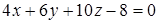 ; ;
|
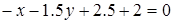 ; ;
|
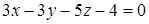 ; ;
|
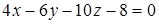 ; ;
|
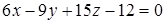 . .
|
Угол между плоскостями 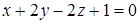 и
и 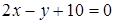 равен…
равен…
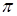 ; ;
| 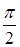 ; ;
| 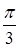 ; ;
| 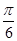 ; ;
| 0. |
Выберите ответ, в котором записано уравнение прямой, проходящей через точки  (3, -2, 4) и
(3, -2, 4) и 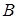 (1, 0, 5).
(1, 0, 5).
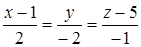 ; ;
|
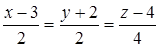 ; ;
|
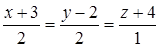 ; ;
|
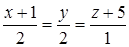 ; ;
|
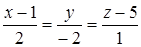 . .
|
Какой смысл имеют параметры 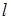 ,
, 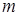 и
и 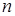 в каноническом уравнении прямой:
в каноническом уравнении прямой: 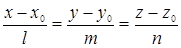 ?
?
это координаты точек, в которых прямая пересекает оси 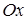 , , 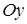 и и 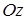 ; ;
|
| это координаты направляющего вектора, параллельного данной прямой; |
| это координаты направляющего вектора, перпендикулярного данной прямой; |
| это координаты точки, через которую проходит данная прямая; |
| это направляющие косинусы. |
Какие параметры в общем уравнении кривой второго порядка 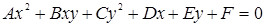 не могут одновременно равняться нулю?
не могут одновременно равняться нулю?
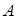 и и 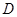 ; ;
| 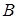 и и 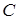 ; ;
| 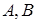 и и 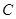 ; ;
| 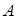 и и 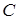 ; ;
| 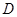 и и 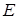 . .
|
Уравнение 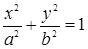 задаёт:
задаёт:
| окружность | эллипс | гиперболу | параболу | пустое множество |
Уравнение 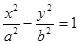 задаёт:
задаёт:
| окружность | эллипс | гиперболу | параболу | пустое множество |
Уравнение 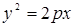 задаёт:
задаёт:
| окружность | эллипс | гиперболу | параболу | пустое множество |
Уравнение 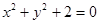 задаёт:
задаёт:
| окружность | эллипс | гиперболу | параболу | пустое множество |
Выбрать ответ, в котором правильно указаны радиус 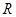 и координаты центра
и координаты центра 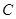 окружности
окружности 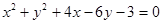 .
.
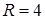 ; ; 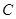 (-2, 3); (-2, 3);
|
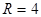 ; ; 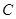 (2, -3); (2, -3);
|
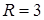 ; ; 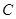 (-2, 3); (-2, 3);
|
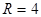 ; ; 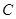 (2, 3); (2, 3);
|
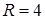 ; ; 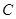 (-2, -3). (-2, -3).
|
| <== предыдущая | | | следующая ==> |
| | | Тема - Нервно-мышечная физиология |
Date: 2015-07-02; view: 5449; Нарушение авторских прав