Смешанное произведение векторов и его свойства

Базис.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

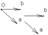Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

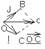ОС = OA + OB, OA =x* i, OB =j*y, OC =x i +y j. Числа х,у наз-ся координатами вектора ОС в данном базисе

Скалярное произведение векторов.

Определение 2: Скалярное произведение ставит в соответствие паре векторов a и b число (a,b)=|a|·|b|·cosφa,b.

Свойства скалярного произведения:

1. коммутативность: (a,b)=(b,a)

2. (а,а)=|а|2

3. (a,b)=0 <=> a b

4. Дистрибутивность: (a1+а2,b)= (a1,b)+ (a2,b)

5. (а, λ·b)= λ·(a,b) λ R.

Утверждение 1: В декартовом базисе если а={x1,y1,z1}, b={x2,y2,z2}, то (a,b)=x1·x2+y1·y2+z1·z2.

Векторное произведение векторов.

Определение 3: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что

| [a,b] |=Sa,b, где Sa,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то Sa,b=0.)

a [a,b] b.

a, b, [a,b] – правая тройка.

Свойства векторного произведения:

[a,b] = -[b,a]

[a,b] = θ ó a || b

[a1+a2,b] = [a1,b]+[a2,b]

λ·[a,b] = [λ·a,b] = [a,λ·b] λ R.

Утверждение 2: В декартовой системе координат (базис i, j, k), a={x1, y1, z1}, b={x2, y2, z2}

=> [a,b]=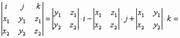

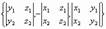
Смешанное произведение векторов и его свойства.

Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a * b * c =[ a * b ]* c = a *[ b * c ], где

a ={a_x,a_y,a_z}

b ={b_x,b_y,b_z}

c ={c_x,c_y,c_z}

Св-ва:
1. При перестановке 2х сомножителей:

a * b * c =- b * c * a

2. не меняется при перестановке циклических сомножителей:

a * b * c = c * a * b = b * c * a

3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a * b * c =0

б)если некомпланарные вектора a, b, c привести к 1 началу, то | a * b * c |=Vпараллепипеда, построенного на этих векторах

если a * b * c >0, то тройка a, b, c - правая

если a * b * c <0, то тройка a, b, c - левая

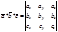
Date: 2015-07-02; view: 318; Нарушение авторских прав