Момент инерции двух полых цилиндров

Цель работы.

Определить: 1) угловой коэффициент упругости спиральной пружины;

момент инерции двух полых цилиндров.

Проверить аддитивность момента инерции и теорему Штейнера.

Оборудование. В комплект экспериментальной установки входят: вращающийся вал, на который устанавливают стержень или диск; два полых толстостенных цилиндра; динамометр; масштабная линейка; световой барьер со счетчиком; источник питания (рис.1).

Рис. 1. Внешний вид установки

Закрепим диск на вращающийся вал и повернем его на угол j₀ » 90°. Если предоставить систему самой себе, то в ней возникнут свободные крутильные колебания: потенциальная энергия спиральной пружины будет переходить в кинетическую энергию диска и наоборот. В реальных условиях под действием моментов сил трения в подшипниках и сопротивления воздуха диск совершает затухающие колебания. При слабом затухании в пределах одного периода потерями механической энергии можно пренебречь, ввиду их малости, а закон сохранения механической энергии имеет вид

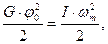(1)

где: G- угловой коэффициент упругости спиральной пружины; I-момент инерции диска; w_m – максимальная угловая скорость диска.

При слабом затухании механические колебания можно считать гармоническими. Угловое перемещение j в момент времени t описывает-ся уравнением

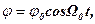(2)

где W₀ - собственная циклическая частота свободных колебаний диска.

Циклическая частота связана с периодом Т свободных колебаний соотношением

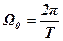. (3)

Модуль угловой скорости маятника определим как первую производную от углового перемещения (2)

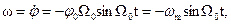(4)

где 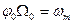- максимальная угловая скорость диска. (5)

Если подставить максимальную скорость диска в уравнение (1)

,

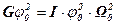то получим формулу, с помощью которой можно определить момент инерции диска

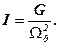(6)

Совместное решение уравнений (3) и (6) позволяет определить момент инерции диска по его периоду крутильных колебаний:

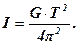(7)

Date: 2015-07-02; view: 336; Нарушение авторских прав