
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема №1. Комплексные числа
|
|
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«ЛИНЕЙНАЯ АЛГЕБРА»
Направление 080100
«Экономика»
Очная форма обучения
Рязань 2012
Тема №1. Комплексные числа
Комплексными числами называют всевозможные упорядоченные пары 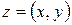 действительных чисел
действительных чисел 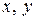 , для которых следующим образом определены операции сложения и умножения:
, для которых следующим образом определены операции сложения и умножения:
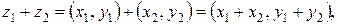 (1.1)
(1.1)
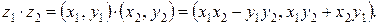 (1.2)
(1.2)
Действительные числа 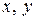 называют соответственно действительной и мнимой частями комплексного числа
называют соответственно действительной и мнимой частями комплексного числа 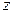 и обозначают
и обозначают 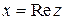 ,
, 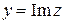 .
.
В декартовой системе координат 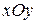 комплексное число
комплексное число 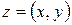 изображается точкой
изображается точкой 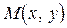 или радиус-вектором
или радиус-вектором 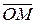 этой точки (см. рис.1.1). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось
этой точки (см. рис.1.1). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось 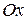 – действительной осью, ось
– действительной осью, ось 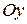 – мнимой осью.
– мнимой осью.
Комплексные числа вида 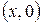 отождествляются с действительными числами
отождествляются с действительными числами 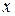 :
: 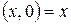 . Тогда умножение действительного числа
. Тогда умножение действительного числа 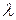 на комплексное число
на комплексное число 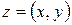 в соответствии с формулой (1.1) дает
в соответствии с формулой (1.1) дает
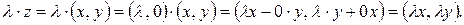 (1.3)
(1.3)
Комплексное число 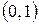 называется мнимой единицей и обозначается символом
называется мнимой единицей и обозначается символом 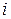 , причем согласно (1.2)
, причем согласно (1.2)
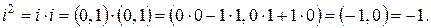
Любое комплексное число 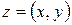 можно представить как
можно представить как
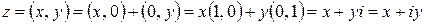 .
.
Запись комплексного числа 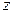 =
= 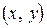 в виде
в виде
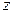 =
= 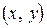 =
= 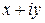 . (1.4)
. (1.4)
называется алгебраической формой комплексного числа.
Комплексное число 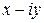 называется сопряженным комплексному числу
называется сопряженным комплексному числу 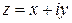 и обозначается символом
и обозначается символом 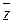 .
.
Для комплексных чисел определены также операции вычитания
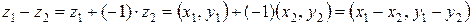
и деления
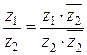 . (1.5)
. (1.5)
При арифметических операциях над комплексными числами, представленных в алгебраической форме (1.4), с ними можно обращаться как с биномами вида 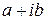 , учитывая дополнительно, что
, учитывая дополнительно, что 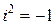 .
.
Пример 1.1. Пусть 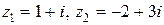 ,
, 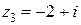 ,
, 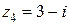 ,
,
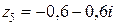 . Вычислить число
. Вычислить число 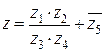 .
.
Решение: Сначала вычислим числитель дроби первого слагаемого
 .
.
Вычислим знаменатель дроби первого слагаемого:
 .
.
Тогда первое слагаемое 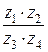 дроби будет вычисляться по формуле (1.5):
дроби будет вычисляться по формуле (1.5):
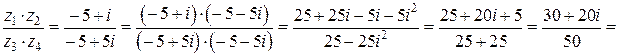
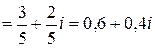 .
.
Окончательно вычисляем число 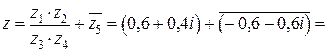
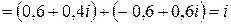 .
.
Любое комплексное число 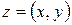 (
(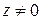 ) можно представить в виде
) можно представить в виде
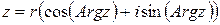 , (1.6)
, (1.6)
где 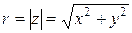 – модуль числа
– модуль числа 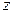 (длина радиус-вектора
(длина радиус-вектора 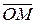 точки
точки 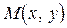 , см. рис. 1.1),
, см. рис. 1.1), 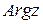 – аргумент числа
– аргумент числа 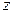 , равный величине угла, на который следует повернуть ось
, равный величине угла, на который следует повернуть ось 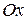 до совпадения с вектором
до совпадения с вектором 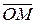 (
(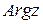 больше нуля, если вращение происходит против часовой стрелки и меньше нуля, если вращение происходит по часовой стрелки);
больше нуля, если вращение происходит против часовой стрелки и меньше нуля, если вращение происходит по часовой стрелки);
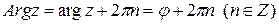 ,
где ,
где 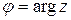 – главное значение аргумента числа – главное значение аргумента числа 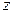 , причем считается, что , причем считается, что
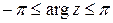 и и
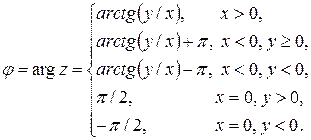
|

|
На практике обычно формулу (1.6) используют в виде
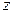 =
= 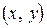 =
= 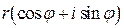 . (1.7)
. (1.7)
Формулы (1.6), (1.7) называют тригонометрической формой записи комплексного числа.
Тригонометрической формой записи удобно пользоваться, если необходимо возвести комплексное число 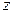 =
= 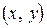 в натуральную степень
в натуральную степень 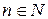 . Для
. Для
этого используется формула Муавра возведения в степень:
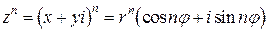 . (1.8)
. (1.8)
Пример 1.2. Вычислить 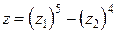 , если
, если 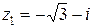 ,
, 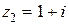 .
.
Решение: Сначала найдем 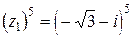 . Число
. Число 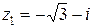 представим в тригонометрической форме (1.7). Для этого находим модуль
представим в тригонометрической форме (1.7). Для этого находим модуль 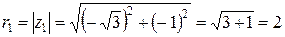 и главное значение
и главное значение 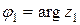 :
:
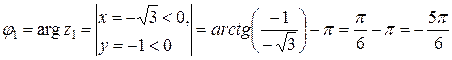 .
.
Тогда 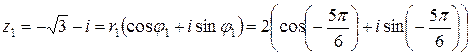 .
.
По формуле Муавра (1.8) имеем 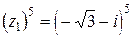 =
=
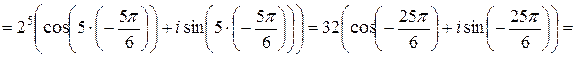
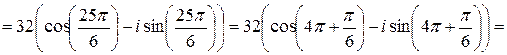
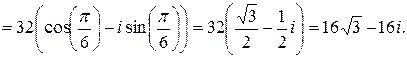
Аналогично вычисляем 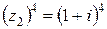 . Для числа
. Для числа 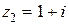 модуль
модуль 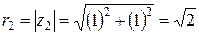 , главное значение аргумента
, главное значение аргумента 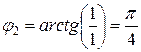 ,
,
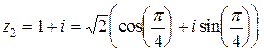 .
.
По формуле Муавра (1.7) имеем
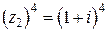
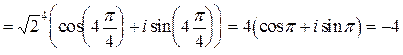 .
.
Окончательно имеем 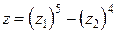 =
= 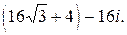
Для извлечения корня натуральной степени 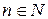 из комплексного числа
из комплексного числа 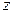 =
= 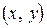 используется формула
используется формула
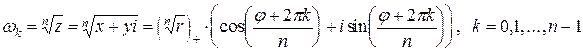 , (1.9)
, (1.9)
где 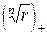 означает арифметический корень
означает арифметический корень 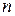 -ой степени из действительного
-ой степени из действительного
положительного числа. Число различных корней 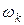 равно
равно 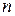 .
.
Пример 1.3. Найти 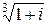 .
.
Решение: Используем представление числа 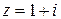 в тригонометрической форме (см. пример 1.2)
в тригонометрической форме (см. пример 1.2) 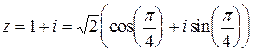 . Применяя формулу (1.9), получим (
. Применяя формулу (1.9), получим (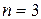 )
)
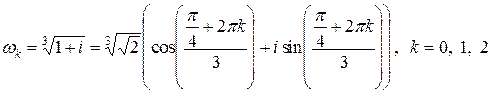 . (1.10)
. (1.10)
Отдельно подсчитаем все 3 корня 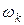 (для этого в формуле (1.10) берем соответственно
(для этого в формуле (1.10) берем соответственно 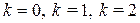 ):
): 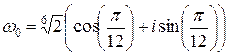 ,
,
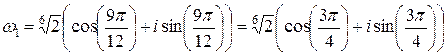 ,
,
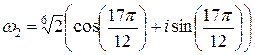 .
.
Все три корня можно представить в алгебраической форме, используя формулы половинного аргумента 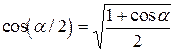 ,
,  , а также формулы приведения. Вычисляем
, а также формулы приведения. Вычисляем
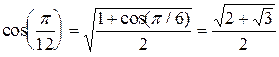 ,
, 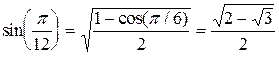 ,
,
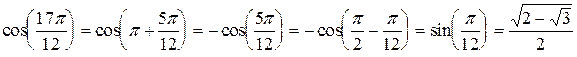 ,
,
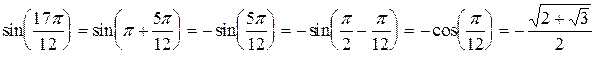
и подставляем в числа 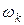 .
.
Отметим все три полученных числа 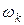 на координатной плоскости. Заметим, что все они имеют один и тот же модуль, равный
на координатной плоскости. Заметим, что все они имеют один и тот же модуль, равный 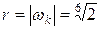 , то есть они лежат на окружности радиуса
, то есть они лежат на окружности радиуса 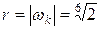 с центром в начале координат. Аргумент числа
с центром в начале координат. Аргумент числа 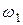 , как нетрудно видеть отличается от аргумента числа
, как нетрудно видеть отличается от аргумента числа 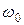 на угол, равный
на угол, равный 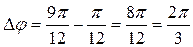 (аналогично с числами
(аналогично с числами 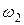 и
и 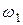 ).
).
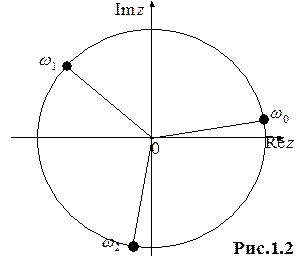
|
Изобразив число 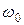 на координатной плоскости, повернем его радиус вектор на угол
на координатной плоскости, повернем его радиус вектор на угол 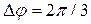 против часовой стрелки и получим число
против часовой стрелки и получим число 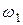 ; повернув радиус-вектор числа
; повернув радиус-вектор числа 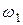 на угол
на угол 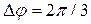 опять против часовой стрелки, получим число
опять против часовой стрелки, получим число 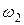 (см. рис. 1.2).
(см. рис. 1.2).
Иногда комплексное число 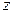 =
= 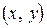 , записанное в тригонометрической форме (1.7), представляют в показательной форме
, записанное в тригонометрической форме (1.7), представляют в показательной форме
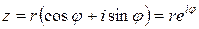 . (1.11)
. (1.11)
Date: 2015-07-02; view: 476; Нарушение авторских прав