Основные задачи динамики

Первая или прямая задача:

Известна масса точки и закон ее движения, необходимо найти действующую на точку силу.

m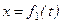

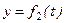
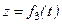
Вычисляем вторые производные по времени от координат точки, умножаем их на массу и получаем проекции силы на оси координат

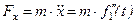
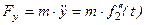
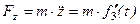
Зная проекции силы на оси координат, определяем модуль силы и ее направляющие косинусы:

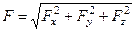
Пример 1: Движение точки в плоскости xOy определяется уравнениями:

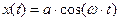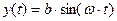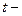; ; ; время.

Решение: ;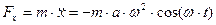

;

; .

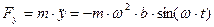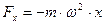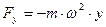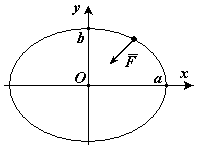
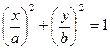- Уравнение траектории в координатной форме (эллипс).

;

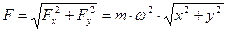
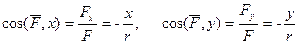
Пример 2: Точка, имеющая массу 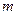, движется из состояния покоя по окружности радиуса 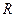с постоянным касательным ускорением 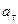. Определить действующую на точку силу в момент, когда она пройдет по траектории расстояние .

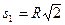Решение: Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:

; ; ;

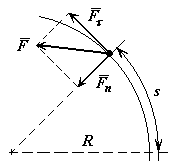
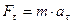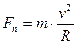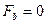Так как 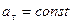, то ,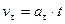

; ;

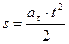
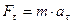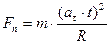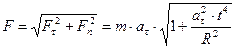
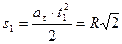; следовательно ;

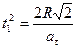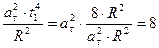; следовательно

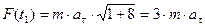
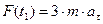
Вторая или обратная задача:

Известна масса точки и действующая на точку сила, необходимо определить закон движение этой точки.

Рассмотрим решение этой задачи в декартовой системе координат. Сила зависит от времени, координат точки, ее скорости и других причин.

, ,

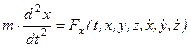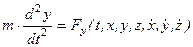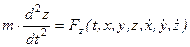
Из теории обыкновенных дифференциальных уравнений известно, что решение одного дифференциального уравнения второго порядка содержит две произвольные постоянные. Для случая системы трех обыкновенных дифференциальных уравнений второго порядка имеется шесть произвольных постоянных:

Каждая из координат 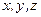движущейся точки после интегрирования системы уравнений зависит от времени и всех шести произвольных постоянных, т.е.

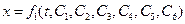
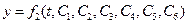
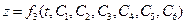
К этим уравнениям необходимо добавить начальные условия:

,

,

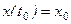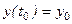
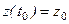
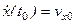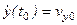
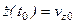
Используя эти начальные условия можно получить шесть алгебраических уравнений для определения шести произвольных постоянных .

Date: 2015-07-02; view: 369; Нарушение авторских прав