Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Типи теорем
|
|
Ще у школі ми зустрічалися з різними видами теорем: пряма, обернена, протилежна, протилежна до оберненої. Розглянемо їх з точки зору математичної логіки.
З'ясуємо логічну суть цих термінів. Якщо пряме твердження мовою логіки записати у вигляді формули
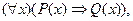(1)
то твердження 
(2)
називають оберненим до (1);
твердження 
(3)
протилежним до (1),
а твердження 
(4)
протилежним твердженню, оберненому до (1).
Інтуїтивно зрозуміло, що речення (1) — (4) не завжди одночасно істинні, тобто не завжди є правильними теоремами.
Теорема 1(Пряма): за допомогую символів математичної логіки її можна записати так: (
х є N) (Р (х) 
Q(х))
Приклад: Якщо сума цифр числа ділится на 3, то і число ділиться на 3.
х є N – теорема справедлива для всіх натуральних чисел.
Р (х) – умова теореми: „Сума цифр числа х: 3”.
Q(х) - висновок теореми: „Число х ділиться на 3 ”.
Поміняємо місцями умову і висновок без зміни пояснювальної частини одержимо обернену теорему.
Теорема 2 (Обернена ): за допомогую символів матлогіки вона записується так ( х є N) (Q (х) Р (х))
Приклад: Якщо число ділиться на 3, то сума цифр цього числа ділиться на 3.
Якщо в прямій теоремі умову і висновок замінити їх запереченням, то одержимо теорему протилежну до прямої.
Теорема 3 (Протилежна ): за допомогою символів матлогіки її можна записати так: ( х є N ) (
)
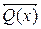Приклад: Якщо сума цифр даного числа не ділится на 3, то число не ділиться на 3.
Якщо в оберненій теоремі умову і висновок замінити їх запереченнями, то одержимо теорему протилежну до оберненої.
Теорема 4 (Протилежна до оберненої): символічно вона записуєтся так: ( х є N) ( )
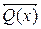
Приклад: Якщо число не ділиться на 3, то й сума цифр цього числа не ділиться на 3.
Теорема 5. З істинності прямої теореми не випливає істинність оберненої до неї теореми.
Доведення. Для доведення цього твердження достатньо за означенням логічного наслідку показати, що формула 
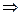
не є загальнозначущою на довільній множині М. Справді, якби це було не так, то для довільного фіксованого елемента а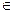 
М висловлення 
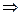
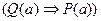було б істинним, а це не правильно, бо: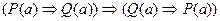 
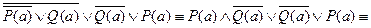
оскільки при Р (а) = 0 і Q (а) = 1 ця формула хибна.
Теорему доведено.
Обґрунтований факт показує, що коли ми спромоглися довести пряму теорему, то про істинність оберненої донеї теоремими нічого конкретного не можемо сказати: вона може бути водних випадках істинною, в інших — хибною. Звідси випливає, що в кожному конкретному випадку, коли требадослідити обернену до даної теореми, її формулюють, апотім доводять чи спростовують.
Теорема 6. Пряма теорема і обернена до протилежної є рівносильними між собою твердженнями.
Доведення. Для обґрунтування цього факту нам, по суті, потрібно показати, що 
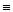
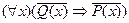. У даному випадку це зробити дуже просто. Справді, оскільки 
і 
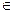при будь-якому х М, то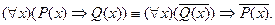 
Цей висновок дає змогу з істинності одного твердження автоматично робити висновок про істинність другого твердження. У логіці цей факт відомий під назвою закону контрапозиції: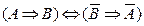 
Теорему доведено.
Через те, що будь-яку з теорем (1) — (4) можна назвати прямою, то з теорем 5 і 6 випливають такі наслідки:
1) 3 істинності оберненої теореми не випливає істинність відповідної їй прямої теореми.
2) Протилежна прямій теорема і обернена до прямої теорема — рівносильні між собою математичні речення.
3) 3 істинності протилежної прямій теореми не випливає істинність протилежної до оберненої теореми.
Теореми умовно поділяють на прості і складені. Теорема вважається простою, коли обидва предикати Р(х) і Q(x) є елементарними. В усіх інших випадках теорема вважається складною. Інколи доведення складної теореми можна замінити доведенням кількох, взагалі кажучи, простих теорем.
Date: 2015-07-02; view: 618; Нарушение авторских прав