Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Законы алгебры-логики
|
|
Аксиомы и законы алгебры
Аксиомы дизъюнкции.
1. X +0= X. Действительно, если X =0, то 0+0=0, а если X =1, то 1+0=1.
2. X +1=1 - при любом X все определяет 1.
3. X + X = X - 0+0=0, 1+1=1.
4. 
.
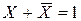Аксиомы конъюнкции.
1. X 0=0 - 00=0, 10=0.
2. X 1= X - 01=0, 11=1.
3. XX = X - 00=0, 11=1.
5. 
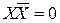- 01=0, 10=0.
Аксиомы под номером 1 называют теоремой объединения, под номером 2 - пересечения, 3 - закон тавтологии, 4 - закон дополнительности.
Аксиомы инверсии.
1. 
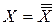. Словами: " X - это НЕ НЕ Х".
2. 
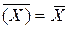. Словами: "НЕ от X это НЕ X ".
Законы алгебры-логики
1. Закон коммутативности, или переместительный закон
, 
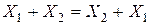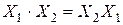
Справедливость законов можно подтвердить путем подстановки непосредственно значений аргументов, т. е. 1 и 0, перебрав все комбинации.
С точки зрения электроники этот закон позволяет подавать сигналы на любые входы элемента.
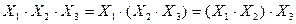2. Закон ассоциативности или сочетательный закон
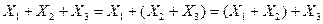
3. Закон дистрибутивности или распределительный закон
.
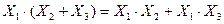
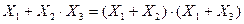Последняя запись не имеет аналога в математике. Но его справедливость можно доказать. Исходя из справедливости 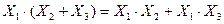для любых значений переменных Х1, Х2 и Х3 используем принцип двойственности для изменения формы записи левой и правой частей. В результате получим: 
. Введем новые обозначения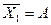 
, 
, 
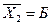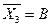и получим А+БВ=(А+Б)(А+В), что полностью совпадает с второй формой записи закона дистрибутивности.
4. Закон поглощения или избыточности
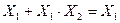, а в двойственной форме 
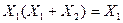. Докажем. 
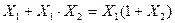- по аксиоме пересечения 
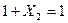и 
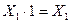, то 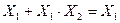. Соответственно для второго 
.
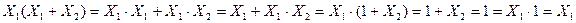5. Закон склеивания
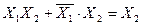
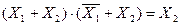
Первому члену можно поставить в соответствие лист бумаги, на одной стороне которого написано Х1, а на другой стороне Х2. Второму члену соответствует лист с надписями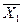 
и Х2. При склеивании клеем заклеивается меняющаяся величина Х1. Докажем эти соотношения
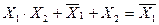
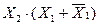т.к. 
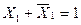, то
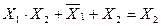
Аналогично
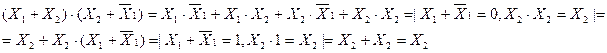
6. Правило де Моргана
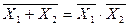- отрицание дизъюнкции есть конъюнкция отрицаний.
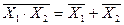- отрицание конъюнкции есть дизъюнкция отрицаний
Справедливость вытекает из принципа двойственности: т.е. получая из ИЛИ И путем замены переменных на инверсные и знака (+) на (*).
Так для нескольких переменных правило будет
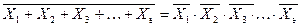
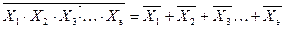или
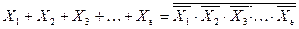
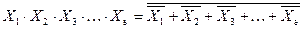
Справедливость законов можно подтвердить и путем подстановки непосредственных значений аргументов, т.е. 0 или 1, перебрав все комбинации.
| <== предыдущая | | | следующая ==> |
| Глава 5. Типичные ошибки в языке и стиле деловой корреспонденции | | |
Date: 2015-07-02; view: 346; Нарушение авторских прав