Комплексное число – упорядоченная пара чисел

КОМПЛЕКСНЫЕ ЧИСЛА

I = a + j·b,

где a, b – вещественные числа; j – мнимая единица (в математике обозначают i). По определению j = √-1

Форма записи комплексного числа a + jb называется алгебраической, где a называется действительной частью комплексного числа; b – мнимой частью комплексного числа. Чтобы не путать комплексные числа с действительными числами комплексные числа подчёркиваются, например U.

Геометрическая интерпретация комплексного числа – точка (или вектор) на плоскости.

По оси абсцисс расположена ось действительных чисел (положительное направление обозначено +1), а по оси ординат – ось мнимых чисел (положительное направление обозначено +j).

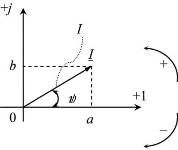
Проекция вектора на ось +1 – действительная часть, а проекция на ось +j – мнимая часть. Таким образом, алгебраическая форма записи соответствует декартовой (прямоугольной) системе координат (обозначим её xy).

Этот же вектор может быть задан и в полярной системе координат. То есть через длину вектора I и угол поворота ψ (обозначим её rθ). Полярной системе координат соответствует показательная форма записи комплексного числа

I = Iejψ,

где I – модуль комплексного числа; ψ – аргумент (или попросту угол)

Обе формы записи (алгебраическая и показательная) используются при расчётах: складывать и вычитать комплексные числа удобно в алгебраической форме записи, а делить и умножать – в показательной. Следовательно, нужно уметь переводить комплексные числа из алгебраической формы записи в показательную (→rθ) и из показательной в алгебраическую (→xy).

Пусть комплексное число задано в алгебраической форме I = a + jb, а требуется найти модуль I и угол ψ. По теореме Пифагора определяем модуль I = √а2 +b2 а угол

ψ = arctan (b/a)

(если a < 0, то к результату надо прибавить (отнять) 180°).

Обратный переход из показательной формы в алгебраическую производят по

формуле Эйлера. Пусть комплексное число задано в показательной форме

I = Iejψ, а требуется найти действительную a и мнимую b части. Из того же рисунка видно, что прилежащий катет a это произведение гипотенузы I на косинус угла ψ, а противолежащий катет b это произведение гипотенузы I на синус угла ψ. Таким образом I =Iejψ = I cos ψ + j I sin ψ.

Основные операции с комплексными числами

Date: 2015-07-02; view: 638; Нарушение авторских прав